자료구조
무수한 상황에서 데이터를 효율적으로 다룰 수 있는 방법을 모아 자료구조라는 이름을 붙였다고 한다.
많은 방법 중, 가장 많이 쓰이고 알고리즘 테스트에 자주 등장하는 Stack, Queue, Tree, Graph를 학습했다.
대부분의 자료구조는 특정 상황에 놓인 문제를 해결하는 데 특화되어 있다. 많은 자료구조를 알아두면 어떤 상황이 닥쳤을 때 적합한 자료구조를 빠르고 정확하게 적용해 문제를 해결할 수 있다.
Stack
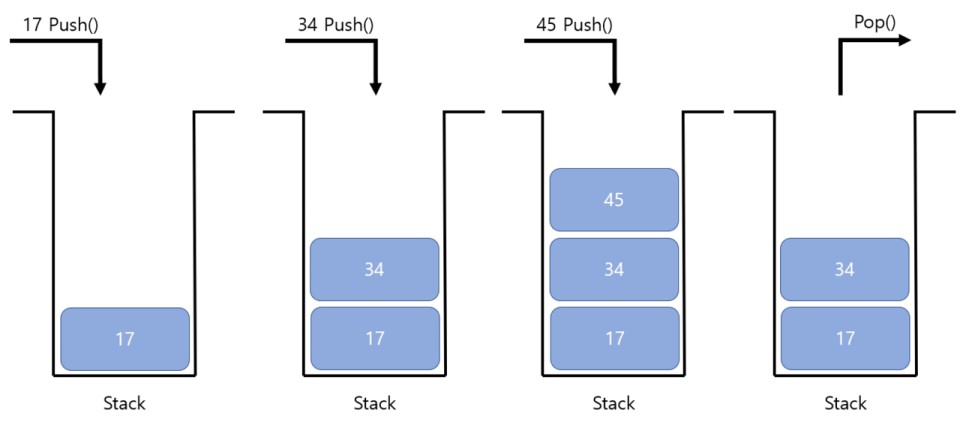
Stack은 쌓다, 쌓이다, 포개지다 와 같은 뜻을 갖고 있다. 데이터를 순서대로 쌓는 구조다.
일상생활에서 Stack의 예를 쉽게 찾아볼 수 있는데, 접시를 생각해보자.

접시를 쌓는다고 생각해보자. 가장 먼저 내려놓은 접시가 맨 아래에 위치해있고, 가장 나중에 내려놓은 접시가 맨 위에 위치하게 된다.
이렇게 쌓아둔 접시를 사용할 땐, 맨 위에 위치한 접시 즉, 가장 나중에 내려놓은 접시를 먼저 사용하게 된다.
Stack의 특징은 입력과 출력이 하나의 방향으로 이루어지는 제한적 접근이다. 이러한 자료구조의 정책을 LIFO(Last In First Out = 후입선출) 혹은 FILO(First In Last Out = 선입후출) 이라 부르기도 한다.
Stack에 데이터를 넣는 것을 Push, 데이터를 꺼내는 것을 Pop이라 한다.
우리가 자주 사용하는 브라우저의 뒤로 가기, 앞으로 가기 기능을 구현할 때 Stack이 활용된다.
Queue
Queue는 줄을 서서 기다리다, 대기행렬 과 같은 뜻을 갖고 있다.

이번에는 자판기를 생각해보자. 자판기에 음료를 채워 넣을 때, 자판기의 뒷판을 열어 음료를 순서대로 넣을 것이다. 이때, 먼저 넣은 음료가 가장 앞에 위치하게 될 것이고, 자판기에 돈을 넣고 음료를 결제하면 가장 앞에 있던 음료가 나오게 될 것이다.
마트나 편의점의 진열대도 비슷하다. 먼저 들어온 식품을 앞에 진열하고, 나중에 들어온 식품을 뒤쪽에 진열하는 선입선출 방법을 사용한다.
Queue는 Stack과 반대되는 개념이다. 먼저 들어간 데이터가 먼저 나오는 FIFO(First In First Out = 선입선출) 혹은 LILO(Last In Last Out = 후입후출)을 특징으로 갖고 있다.
Queue에 데이터를 넣는 것을 enqueue, 데이터를 꺼내는 것을 dequeque라고 한다.
Tree
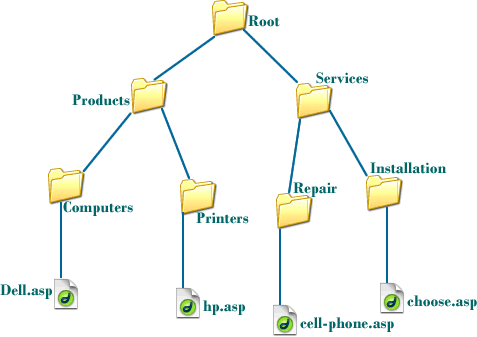
트리구조는 나무를 거꾸로 뒤집어 놓은 듯한 모습을 갖고 있다고 하여 트리구조라고 불린다. 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮았다며 트리 구조라는 이름이 되었다고 한다.
나는 트리구조가 크리스마스 트리를 더 닮았다고 생각한다.
아무튼, 트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조다. 하나의 데이터 아래, 여러 개의 데이터가 존재할 수 있는 비선형 구조다.
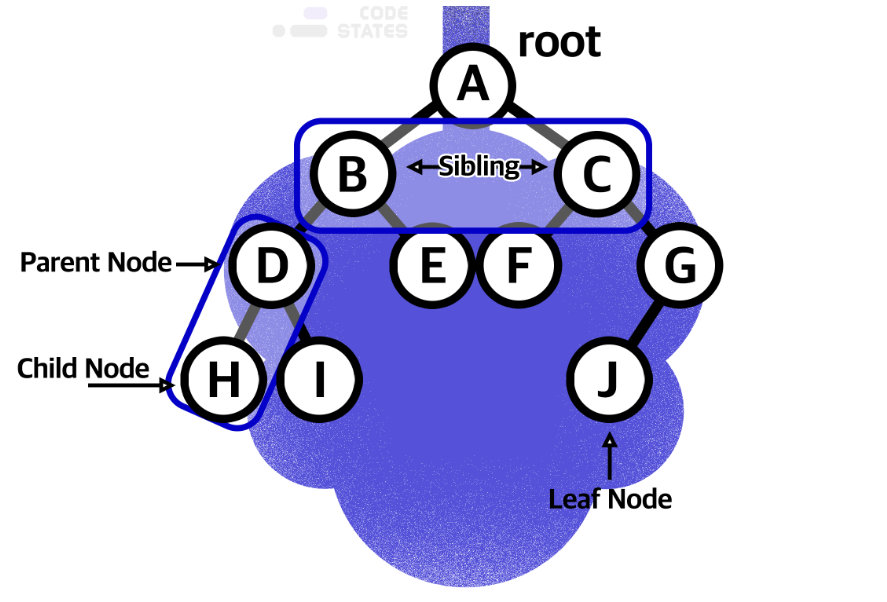
트리 구조는 Root라는 하나의 꼭짓점 데이터를 시작으로, 여러 개의 데이터를 edge로 연결한다. 각 데이터를 Node라 하며, 두 개의 Node가 상하 계층으로 연결되어 부모-자식 관계를 갖는다.
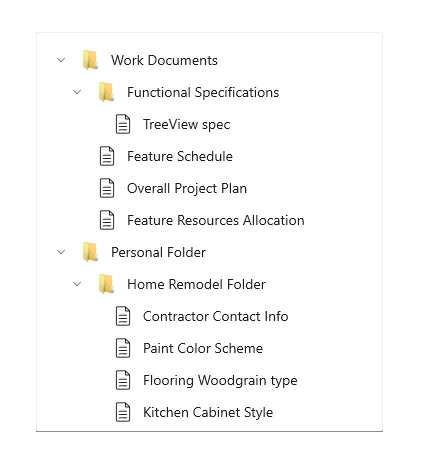
컴퓨터의 파일 탐색기는 우리가 일상생활에서 가장 쉽게 볼 수 있는 트리 구조의 대표적인 예시일 것이다.
하나의 폴더 안에 여러 폴더가 있고, 그 안에 또 다른 폴더나 파일이 있다.
Graph
그래프는 여러 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 것이다.
대부분 위 그림과 비슷한 그래프를 떠올릴 것이다. 컴퓨터 공학에서의 자료구조 그래프는 전혀 다른 모습을 가지고 있다.

자료구조 그래프는 거미줄처럼 여러 점들이 선으로 이어져 있는 복잡한 네트워크망과 같다.
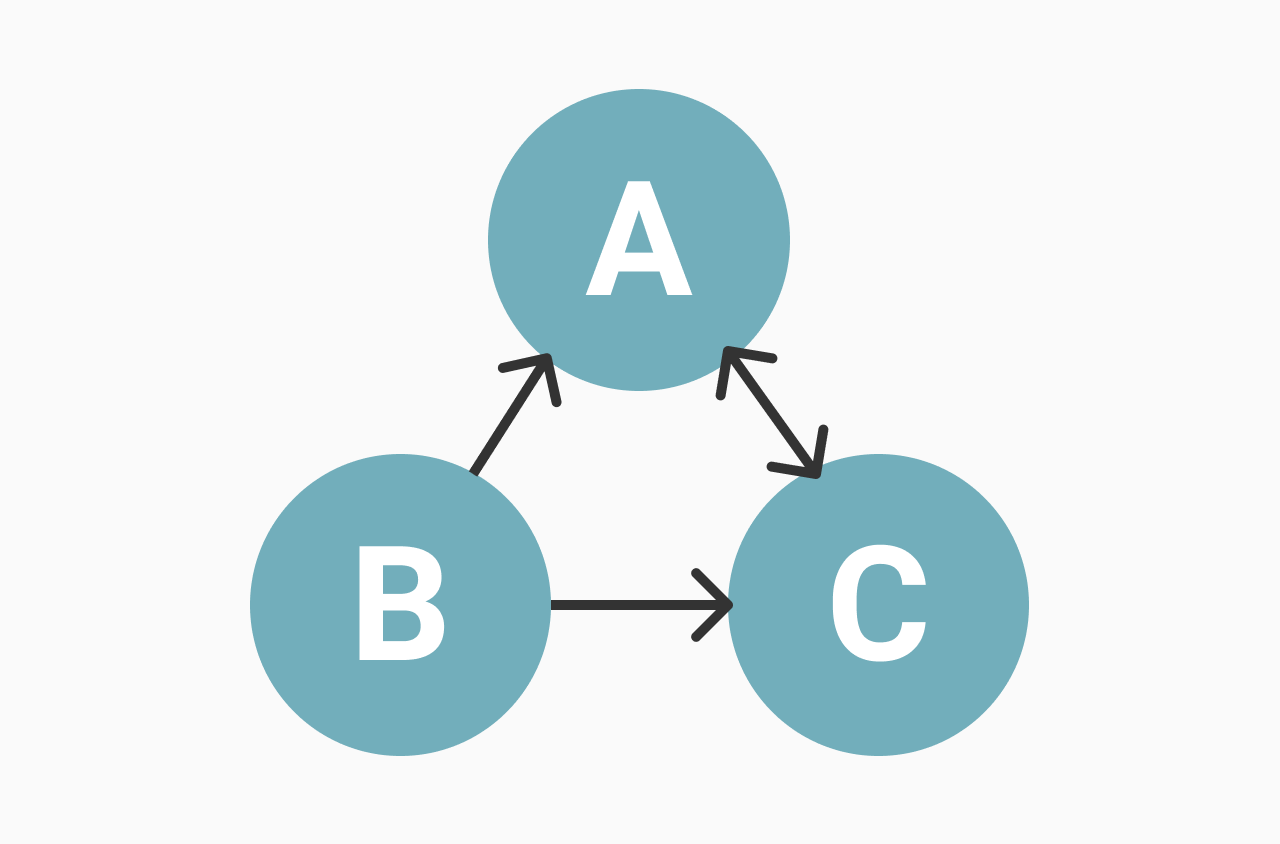
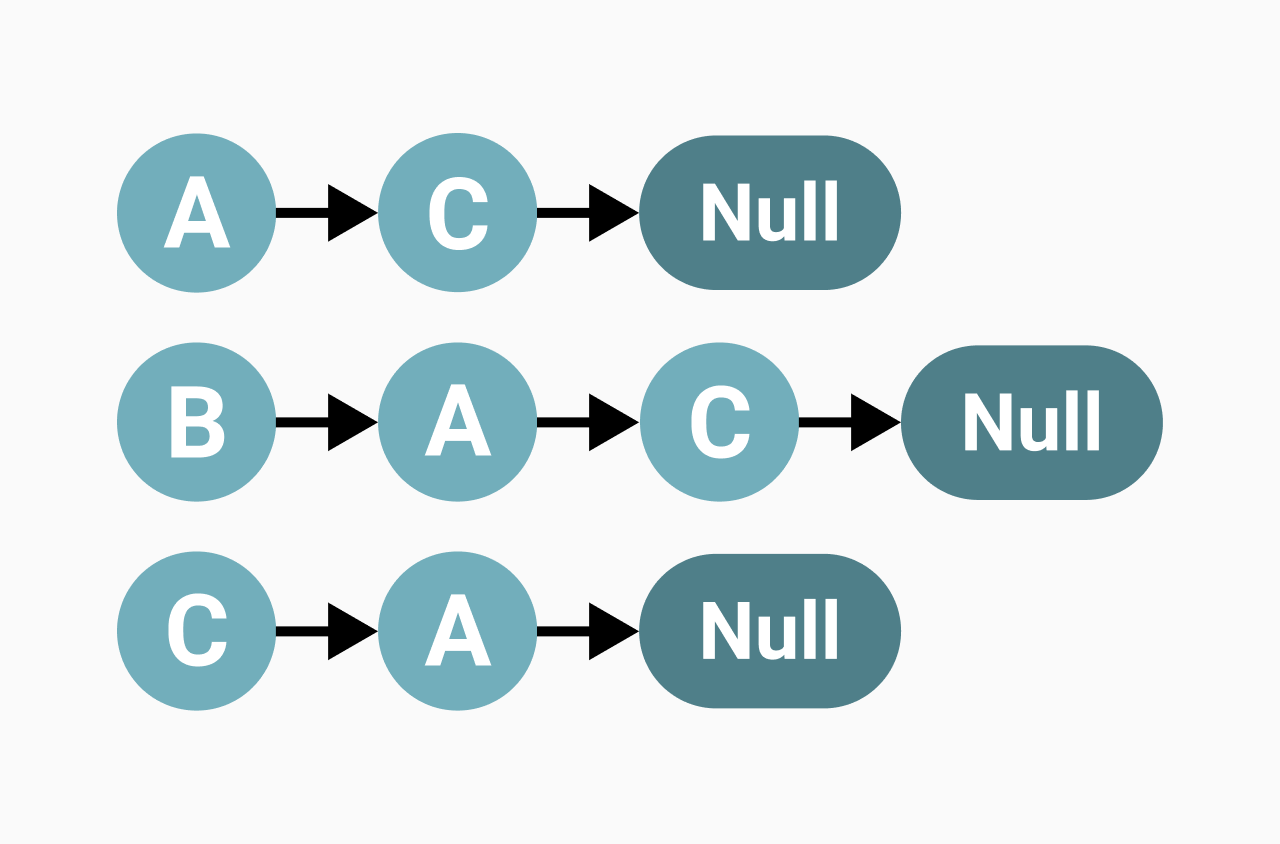
Graph는 직접적인 관계가 있는 경우, 두 점 사이를 이어주는 선이 있다.
간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어진다.
하나의 점을 정점(vertex)이라 표현하고 하나의 선은 간선(edge)이라 표현한다.
위 사진에서 A, B, C는 정점이라 할 수 있고, 그들을 이어주는 화살표는 간선이라 할 수 있겠다.
인접 행렬

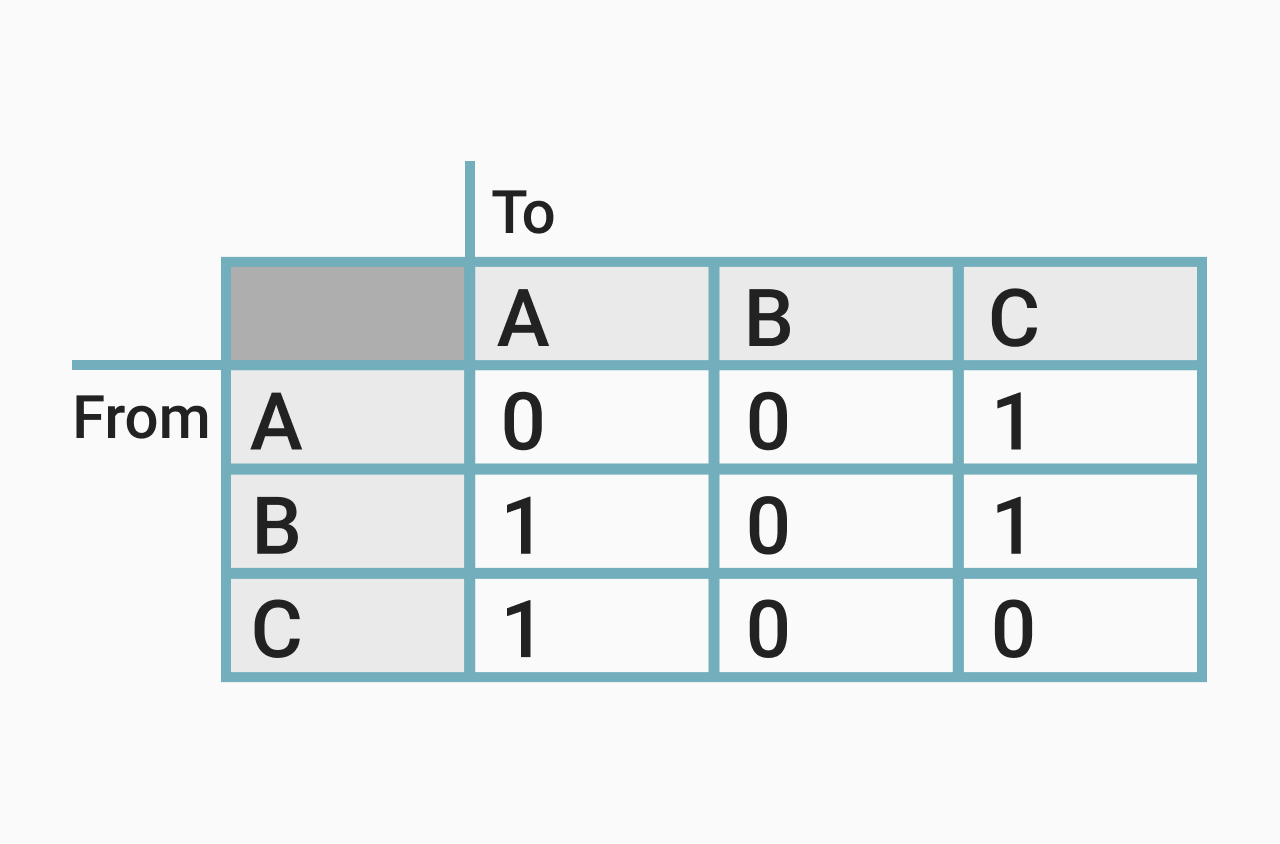
두 정점을 바로 이어주는 간선이 있을 때, 두 정점은 인접하다고 이야기 한다.
인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬도 2차원 배열의 형태로 나타낸다. A와 B 정점이 이어져 있다면 1(true), 그렇지 않다면 0(false)으로 표시한 일종의 표다.
인접 리스트는 각 정점이 어떤 정점과 인접하는지를 리스트 형태로 표현한 것이다.
각 정점마다 하나의 리스트를 갖고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있다. 위의 그래프를 인접 리스트로 표현하면 다음과 같다.