Binary Search Trees(이진 탐색 트리)

이진 탐색 트리

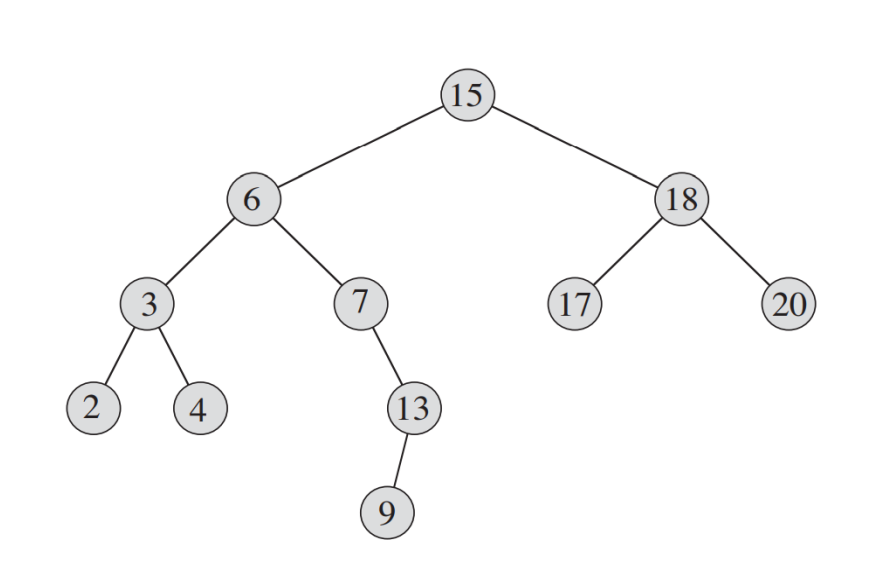
특징

1. 모든 노드들이 자식 노드를 2개 이하로 가진다.
2. 한 노드를 중심으로 그 노드의 키 값보다 작은 것은 왼쪽 서브트리에, 큰 것은 오른쪽 서브트리에 있다.
3. running time은 O(h)이다.
4. Successor: 해당 숫자의 큰 수 중 제일 작은 값.
   만약 해당 노드의 오른 쪽 서브트리가 있다면 ->그 중에서 제일 작은 값 구하기
   없다면 -> 왼쪽으로 계속 올라가서 반대 쪽으로 처음 꺾이는 노드가 successor이다.
5. successor는 자식이 2개일 수 없다.

• 노드 삭제

1. 해당 노드의 자식이 없는 경우 - 그냥 없애기
2. 해당 노드의 자식이 왼쪽만 있는 경우 - 왼쪽과 바꾸기
   해당 노드의 자식이 오른쪽만 있는 경우 - 오른쪽과 바꾸기
3. 자식 둘 다 있는 경우 - 제거하고자하는 노드와 successor의 자리를 바꾼다.

x노드에서 시작해서 'k'라는 키 값을 갖는 노드를 찾는 함수(재귀)

1. x가 널이거나 x.key가 찾고자하는 k값이면
2. x리턴
3. k가 작으면
4. 왼쪽 자식과 비교.
5. k가 크면 오른 쪽 자식과 비교.
Running Time = O(h) (최대로 길게 탐색을 해봤자 트리의 높이기 때문)

x노드에서 시작해서 'k'라는 키 값을 갖는 노드를 찾는 함수(반복)

k값을 발견할 때까지 (해당 노드가 K이거나 null일 때까지 반복한다.)
k가 x.key보다 작으면 x는 왼쪽 자식 노드로 바뀌고, 크면 오른쪽 노드로 바뀌는 과정을 k 값 발견할 때까지 반복한다.

x를 root로 하는 subtree에서 최솟값, 최댓 값 얻기.

TREE-MINIMUN(x) : 트리 root x에서 계속 왼쪽으로 못 내려갈 때까지 내려가다보면 거기에 해당하는 키 값이 최솟 값이다.
TREE-MAXIMUM(x) : 트리 root x에서 계속 오른쪽으로 못 내려갈 때까지 내려가다보면 거기에 해당하는 키 값이 최대 값이다.

Running Time : O(h) (소요시간은 어차피 기껏해봐야 트리 높이 만큼 비교할 수 밖에 없기 때문)