문제 정리
비 내림차순으로 정렬된 배열의 중복을 제거하는 문제입니다.
최종적으로는 총 원소의 개수를 반환하면 됩니다.
풀이
1차 아이디어

배열을 순회하면서 A[i] == A[i+1]일 때 i + 2 이후의 원소들을 모두 왼쪽으로 한칸씩 옮기면 풀 수 있습니다. 이때 시간 복잡도는 O(N^2)가 됩니다.
2차 아이디어
시프팅이 시간 복잡도의 원인이기 때문에 이에 대한 고찰을 해봐야 합니다. 반드시 모든 원소를 옮겨야 할까요?
생각해보면 아닙니다. 원소 삭제하기 문제와 같이 InputIndex을 이용하면 됩니다.
전체적인 과정
- 중복일 때
- 탐색 Index는 +1, 입력 Index는 이동하지 않는다.
- 중복이 아닐 때
- 탐색 Index에 위치한 값을 입력 Index에 위치한 원소에 덮어씌우기
- 탐색 Index와 입력 Index 모두 +1
1) 시작

Index = 0일때는 당연히 중복이 아니기 때문에 입력 Index, 탐색 Index 모두 +1 이동합니다.

위의 과정을 거치면 다음과 같이 되겠죠?
2) 중복일 때

중복인 순간입니다. 이런 경우에는 탐색 index만 +1 이동합니다.

3) 계속 중복이었다가 중복이 아닌 순간..!
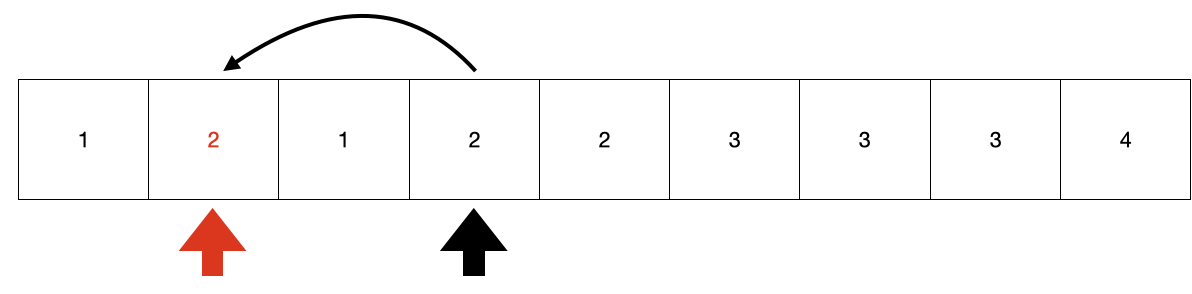
- 계속 중복이기 때문에
탐색 Index만 이동했을겁니다. - 현재 탐색 Index가 가리키는 값을
입력 Index가 가리키는 위치에 덮어 씌웁니다. - 그리고
입력 Index, 탐색 Index모두 +1 이동합니다.
위의 단계들을 탐색 Index 가 끝까지 도달할 때 까지 계속 반복하면 됩니다.
코드
class Solution {
public int removeDuplicates(int[] nums) {
int length = nums.length;
if(length == 0) {
return 0;
}
int inputIndex = 1; // 어짜피 index = 0은 중복이 절대 아니기 때문에 1부터 시작해도 무방.
for (int searchIndex = 1; i < length; i++) {
if (nums[searchIndex] != nums[searchIndex - 1]) {
nums[inputIndex] = nums[searchIndex];
inputIndex++;
}
}
return inputIndex;
}
}