[넘파이(Numpy)]N차원 배열의 형태 변경(2), 전치행렬 - 차원 확대/축소, expand_dims(), squeeze(), arr.T

💡오늘 배울 내용

어느새 넘파이의 거의 마지막 부분을 달리고 있습니다. 오늘은 n차원 배열에서의 형태 변경 두번째 시간으로, 차원을 확대하고 축소하는 함수를 공부해봅시다. 역시 axis가 중요 매개변수로 활용됩니다. 또한 기초 선형대수에서 배웠던 전치행렬을 쉽게 연산하는 방법을 배워봅시다.

🔎expand_dims()

배열의 차원을 확장하는 함수는 expand_dims()입니다. axis=0을 기준으로 차원을 확장할 수도 있고, axis=1을 기준으로 차원을 확장할 수도 있습니다. 각각 어떠한 차이가 있는지에 초점을 맞춰 공부해봅시다.

🔔axis = 0

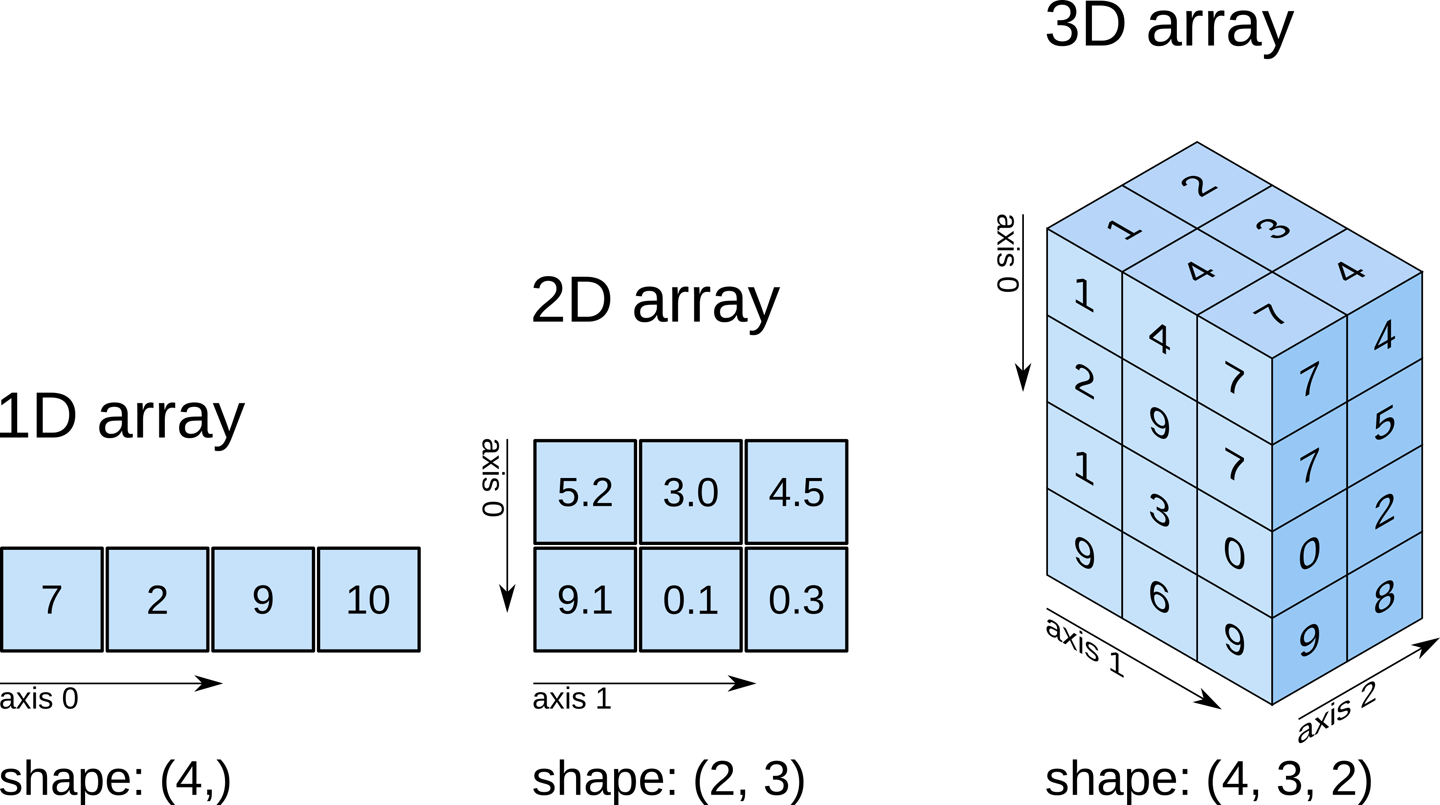
shape에 집중해봅시다.

1차원 배열은 (4, )
2차원 배열은 (2, 3)
3차원 배열은 (4, 3, 2) 임을 확인 할 수 있습니다.

axis 0을 기준으로 한 차원 늘린다는 것은 어떤 의미일까요?
예제를 통해 확인해봅시다.

arr = np.array([1, 2])
print(arr, arr.shape)
>> [1 2] (2,)

arr1 = np.expand_dims(arr, axis=0)
print(arr1, arr1.shape)
>> [[1 2]] (1, 2)

(2, )의 shape을 갖던 1차원 배열을 axis=0을 기준으로 한 차원 늘리면 (1, 2)의 shape을 갖는 2차원 배열이 됩니다.

(2, ) ➡ (1, 2) : expand_dims(axis=0)
즉, shape의 0 위치에 숫자 1을 추가한다고 이해하면 됨.
shape의 (a, b, c, ...)에서 a는 axis0과 관련있고, b는 axis1과 관련있기 때문.

🔔axis = 1

위에 axis를 기준으로 한 차원을 늘린다는 것에 대해 설명했습니다. 예제를 통해 이번에는 axis=1을 기준으로 한 차원 확장에 대해 살펴봅시다.

arr = np.array([1, 2])
print(arr, arr.shape)
>> [1 2] (2,)

arr2 = np.expand_dims(arr, axis=1)
print(arr2, arr2.shape)
>> [[1]
    [2]] (2, 1)

arr를 axis=1을 기준으로 한 차원 확장시킨 배열 arr2의 shape을 확인해보면 (2, 1)이 됨을 알 수 있습니다. 즉, axis 1 위치에 1을 추가한 배열로 변함을 확인할 수 있네요.

🔎squeeze()

배열의 차원을 축소하는 함수는 squeeze()입니다. 마찬가지로 axis를 어떻게 설정하느냐에 따라 축소하는 방법이 다릅니다. 각각 어떠한 차이가 있는지에 초점을 맞춰 공부해봅시다.

🔔axis 0/1

arr = np.array([[1, 2]])
print(arr, arr.shape, arr.ndim)
>> [[1 2]] (1, 2) 2

arr1 = np.squeeze(arr, axis=0)
print(arr1, arr1.shape, arr1.ndim)
>> [1 2] (2,) 1

arr = np.array([[[1], [2], [3]]])
print(arr, arr.shape, arr.ndim)
>> [[[1]
     [2]
     [3]]] (1, 3, 1) 3
     
arr2 = np.squeeze(arr, axis=0)
print(arr2, arr2.shape, arr2.ndim![](https://velog.velcdn.com/images/jhdai_ly/post/72b75976-1da7-41ca-8842-446069816f9e/image.png)

>> [[1]
    [2]
    [3]] (3, 1) 2

배열의 shape이 (a, b, ...)인 경우 axis 0은 a와 관련있고, axis 1은 b와 관련있다는 것을 이해하면 배열의 차원을 줄이는 방법에 대해 쉽게 이해할 수 있습니다. 위의 파이썬 코드에서도 shape이 (1, 2)인 배열을 axis 0을 기준으로 squeeze()했을때 (2, )가 되었습니다.

🔔axis를 입력하지 않으면

axis를 입력하지 않고 squeeze()를 적용하면 무조건 1차원 배열로 줄어듭니다.

arr = np.array([[[1, 2, 3]]])
print(arr, arr.shape, arr.ndim)
>> [[[1 2 3]]] (1, 1, 3) 3

arr1 = np.squeeze(arr)
print(arr1, arr1.shape, arr1.ndim)
>> [1 2 3] (3,) 1

🔎전치행렬 변환

전치행렬은 (Aij)에 대하여 (Aji)로 된 행렬입니다. A^T로 표기합니다.

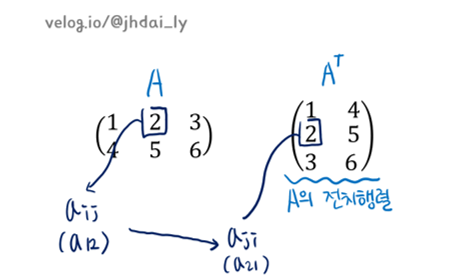
Numpy에서 쉽게 전치행렬을 계산해내는 파이썬 코드 예제를 살펴봅시다.

arr = np.array([[1, 2],
                [3, 4]])
print(arr.T)
>> [[1 3]
    [2 4]]