💡오늘 배울 내용
Numpy의 dot연산을 공부하며, 2차원 배열과 행렬 개념에 대한 공부의 필요성을 느끼게 되었고 해당 부분의 선형대수(행렬) 개념에 대해 학습하게 되었습니다. 행렬 개념과 수반되는 용어 정리, 방정식의 해를 구하는 용도로써의 행렬, 그리고 행렬의 연산을 개념적으로 익혀봅시다.
행렬 2차원 배열 행 열
주대각선 대각성분 영행렬 전치행렬
대칭행렬 정사각행렬 단위행렬 대각행렬
행렬의 연산 행렬곱 가감/상수배
가우스 조던 소거법 역행렬
🔎행렬
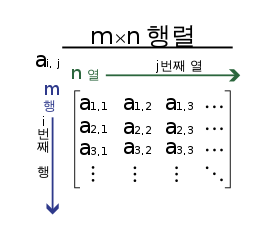
행은 행렬의 가로줄을 말합니다. 열은 행렬의 세로줄을 말합니다.
성분은 행렬 안에 배열된 구성원을 나타내는 말로, 항과 원소라고도 불립니다.
mxn 행렬이란 m개의 행, n개의 열로 이루어진 행렬입니다. (aij)mxn과 같이 표기하기도 합니다.
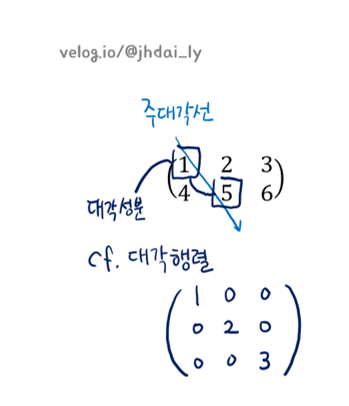
주대각선은 행렬의 가장 왼쪽 상단에서 오른쪽 아래를 가르는 선입니다.
대각성분은 주대각선에 걸치는 행과 열의 지표 수가 같은 성분을 말합니다. cf. (i, i)성분
대각행렬은 주대각선 성분이 아닌 모든 성분이 0인 정사각 행렬입니다.
영행렬은 모든 성분이 0으로 된 행렬입니다.
전치행렬은 (Aij)에 대하여 (Aji)로 된 행렬입니다. A^T로 표기합니다.
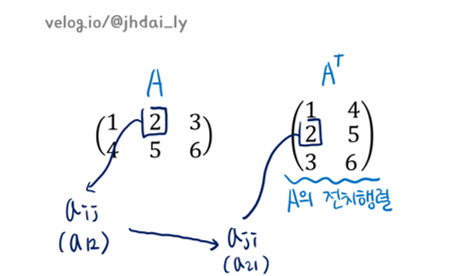
대칭행렬은 A=A^T인 A를 말합니다.
정사각행렬은 행과 열의 개수가 같은 행렬을 말합니다.
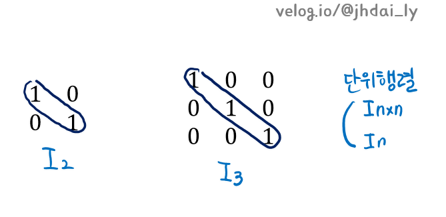
단위행렬은 모든 대각성분은 1, 그 외의 성분은 0인 정사각행렬을 말합니다.
🔎행렬의 연산
행렬의 덧셈과 뺄셈, 상수배 그리고 곱셈에 대해 알아봅시다.
🔔덧셈과 뺄셈
mxn 행렬 A=(aij), B=(bij)에 대해서
행렬 A와 B의 합과 차를 구한다는 것은 같은 성분끼리의 더하고 뺀다는 것을 의미합니다.
즉, A+B = aij + bij
A-B = aij - bij
🔔상수배
mxn 행렬 A=(aij), B=(bij), 그리고 상수 c에 대해
행렬의 상수 배는, 각 성분에 배수 계산을 하는 것입니다.
즉, cA = (caij)
🔔곱셈
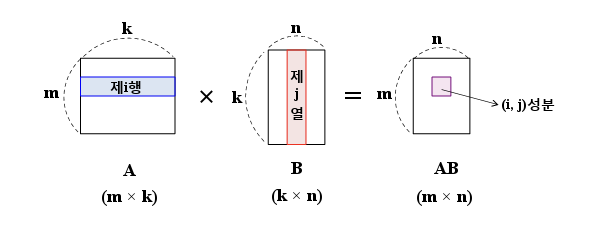
mxn 행렬 A=(aij) 와 nxr 행렬 B=(bjk)에 대해
두 행렬의 곱(AB=Cik)은 Σaijbjk를 의미합니다.
시그마 계산의 아래끝은 j=1, 위끝은 n입니다.
행렬의 곱셈은 일반적으로 교환법칙이 성립하지 않습니다.
행렬 곱 계산이 가능하려면 계산하려는 두 행렬이 mxn, nxr의 모양을 가져야 합니다. 즉, 첫번째 행렬의 열의 길이와 두번째 행렬의 행의 길이가 같아야 합니다.
행렬의 곱셈은 두 함수 f(x, y) = (ax+by, cx+dy), g(x,y) = (px+qy, rx+sy)를 합성한 합성함수 f(g(x, y))와 그 의미가 유사합니다. 즉 함수의 합성과 행렬의 곱셈은 맥을 같이 하고 있습니다.
🔎행렬과 방정식
행렬은 방정식을 풀기 위한 도구로써 사용될 수 있습니다. 연립일차방정식을 예제로 하여 행렬로 방정식을 표시하고, 풀어내는 방법을 익혀봅시다.
🔔방정식의 표현
연립일차방정식은 가우스 조던 소거법과 역행렬을 이용하여 풀어낼 수 있습니다. 즉, 첨가 행렬로 표현하여 가우스 조던 소거법을 적용하거나 등호로 연결된 계수행렬과 상수행렬에 역행렬을 적용하면 됩니다. 아래에서 자세히 살펴보겠습니다.

🔔가우스 조던 소거법
앞에서 첨가행렬로 표현된 연립일차방정식을 가우스 조던 소거법을 통해 풀어낼 수 있다고 하였습니다. 가우스 조던 소거법은 세가지의 기본 행 연산을 통해 연립방정식의 첨가행렬을 기약행사다리꼴로 변환하여 해를 구하는 방법입니다.
세가지의 기본행연산은 다음과 같습니다.
a. 한 행을 상수배 한다.
b. 한 행을 상수배하여 다른 행에 더한다(뺀다)
c. 두 행을 맞바꾼다.
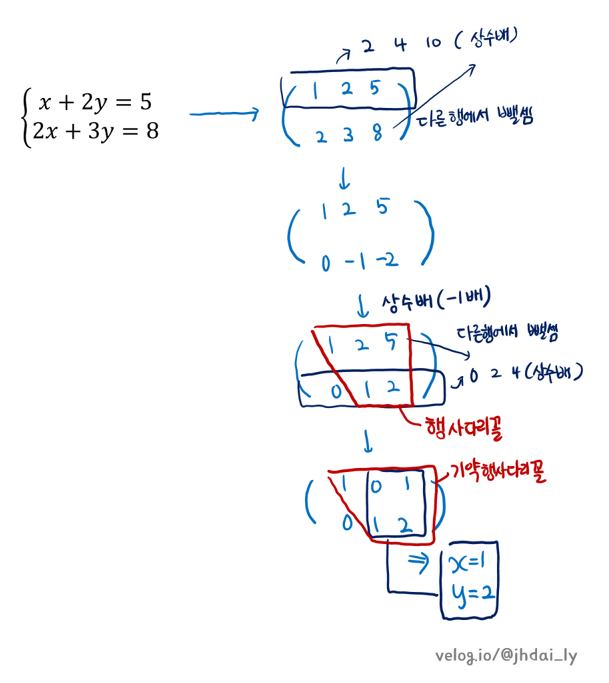
위의 그림은 세가지의 기본 행 연산을 이용하여 연립일차방정식을 풀어내는 과정입니다. 그림에서 행 사다리꼴까지 행렬을 변환하는 과정을 가우스 소거법, 기약 행 사다리꼴까지 변환하는 과정을 가우스 조던 소거법이라고 부릅니다.
🔔역행렬
연립일차방정식 AX = B 에서 A의 역행렬이 존재하면, X = (A^-1) B 입니다.
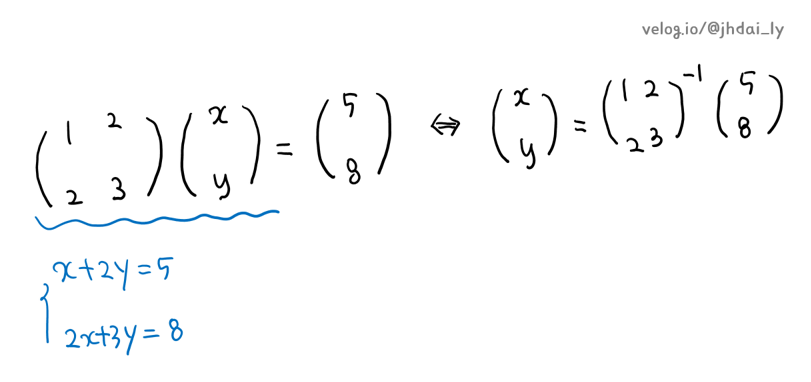
*이상엽 교수님의 선형대수 강의 학습을 진행 후 복습을 위해 작성하였음을 밝힙니다. 예제와 설명이 유사한 부분이 있을 수 있습니다.