
Prefix
전 포스트에서 Classical Computer의 bit를 보았습니다. 이제, quantum bit - qubit을 알아봅시다.
Qubit은 2차원 Hilbert Space 안의 unitary vector입니다. 아주 간단한 정의죠? 2차원이니 basis 가 2개라는 뜻일테고, unitary 라고 했으니 확률 계산이 쉽게 unit vector로 정의한 것 같습니다. Hilbert Space 안에 정의된다는게 저는 익숙치는 않던데, Newtonian Mechanics 를 정의했던 Euclidean Space를 wave의 정확한 계산을 위해 infinite dimension까지 확장한 space입니다.
Space
어차피 저희는 이 시리즈에서 Hilbert Space 밖을 벗어날 일을 없을테지만, Hilbert Space 안에서 정의되는 Vector의 성질을 이해하기 위해서는 저같이 Space 에 대해 잘 모르시는 분들을 위해 개념만 아는 것도 좋을 것 같아요. 사실 infinite dimensional Eucliean Space니까 이 부분은 스킵하셔도 됩니다.
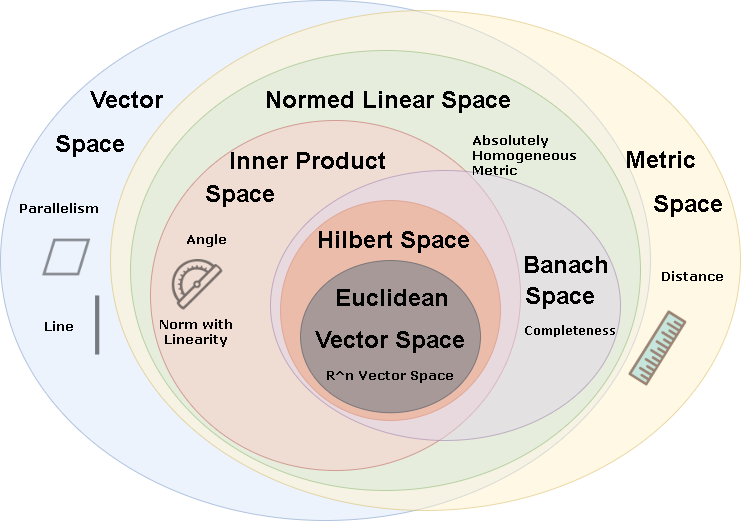
사실 우리에게 익숙한 곳은 Newtonian Mechanics가 적용되는 Euclidean Space 혹은 수학을 배울 때 쓰는 vector space입니다. Wave를 포괄하는 Quantum System을 배우려면 Euclidena Space + Infinity 개념만 추가되면 될 것 같은데 왜 저 중에서 굳이 Hilbert Space일까요?
References:
https://misa-xu.github.io/space/
https://www.youtube.com/watch?v=m0g4qpdCkfE&ab_channel=이상엽Math
https://en.wikipedia.org/wiki/Gelfand%E2%80%93Naimark_theorem
https://physics.stackexchange.com/questions/678152/what-is-the-actual-use-of-hilbert-spaces-in-quantum-mechanics
https://www.physicsforums.com/threads/unbounded-operators-in-qm.667655/
https://physics.stackexchange.com/questions/99542/bounded-and-unbounded-operator
