[BOJ 1309 / C++] 동물원

문제

사자들을 가로와 세로 모두 겹치지 않게 배치하는 경우의 수를 구하는 문제.

• 문제 페이지

키포인트

• 쪼개서 생각하기

  • 문제를 너무 크게 보려고 하면 오히려 어렵게 생각될 수 있다.

  • 각 줄에 어떻게 배치가 되냐에 따라 올 수 있는 경우를 나누어보는 식으로 접근

• <왼쪽, 오른쪽, 안채움>

  • 하나의 줄(가로)에 올 수 있는 경우는 위의 3가지 이다.

  • 그렇다면 이렇게 생각해 볼 수 있다.

    • i번째 줄에 왼쪽에 사자를 배치하면 i-1번째에 올 수 있는 경우는? ==> <오른쪽, 안채움>

    • i번째 줄에 오른쪽에 사자를 배치하면 i-1번째에 올 수 있는 경우는? ==> <왼쪽, 안채움>

    • i번째 줄에 사자를 아무도 배치하면 i-1번째에 올 수 있는 경우는? ==> <왼쪽, 오른쪽, 안채움>

• DP로 만들기

  • i번째 줄에 왼쪽에 사자를 배치하면 i-1번째에 올 수 있는 경우는?을 예로 들자.

  • i-1번째에 <오른쪽, 안채움>의 배치가 나올 수 있다.

  • 그렇다면, i-1번째가 오른쪽으로 채워졌을 때의 경우의 수와 아무것도 안채웠을 때의 경우의 수를 더한 것이 위의 예가 된다.

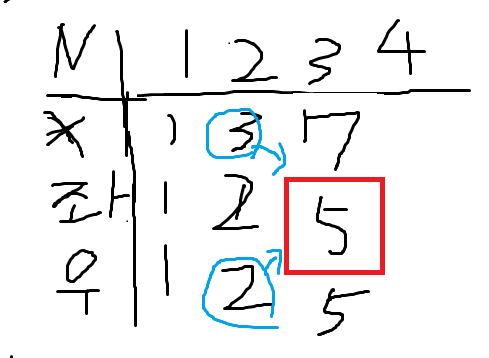
  • dp[i][0] = dp[i][2] + dp [i][0]

  

코드

#include <iostream>

using namespace std;

int N;
int ans;
int res[100002][3];  // 0번째 자리는 쓰지 않음.

int main() {
	cin >> N;

	res[1][0] = 1;  // 0번째: 아무 것도 배치 안할 때의 경우의 수
	res[1][1] = 1;  // 1번째: 왼쪽칸에만 배치 되었을 때의 경우의 수
	res[1][2] = 1;  // 2번째: 오른쪽칸에만 배치 되었을 때의 경우의 수

	for (int i = 2; i <= N; i++) {
		res[i][0] = (res[i - 1][0] + res[i - 1][1] + res[i - 1][2]) %9901;		// i번째 칸에 아무 것도 배치가 안된다면, i-1칸에는 <왼쪽, 오른쪽, 안채움>이 모두 올 수 있음.
		res[i][1] = (res[i - 1][0] + res[i - 1][2]) %9901;		// i번째 칸에 <왼쪽>이 온다면, i-1칸에는 <오른쪽, 안채움>이 올 수 있음.
		res[i][2] = (res[i - 1][0] + res[i - 1][1]) % 9901;		// i번째 칸에 <오른쪽>이 온다면, i-1칸에는 <왼쪽, 안채움>이 올 수 있음.
	}

	ans = (res[N][0] + res[N][1] + res[N][2]) % 9901;		// 사자를 배치할 수 있는 모든 경우의 수

	cout << ans << endl;


	return 0;
}

느낀점

DP는 정말 많이많이 풀어봐야지 될 것 같다는 생각이 든다.

감을 잡기도 힘들고 생각해내기가 어렵다...

똑같은 계산을 반복하는 부분이 있나 잘 찾아내보자.