Q. 개념

---

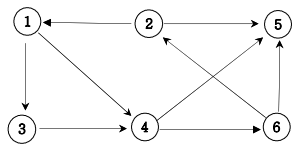
다음 그래프에서 1번 정점에서 각 정점으로 가는 최소 이동 간선수를 출력하세요.
1 2 5
3 4 6

▣ 입력설명
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연
결정보가 주어진다.

▣ 출력설명
1번 정점에서 각 정점으로 가는 최소 간선수를 2번 정점부터 차례대로 출력하세요.

▣ 입력예제 1
6 9
1 3
1 4
2 1
2 5
3 4
4 5
4 6
6 2
6 5

▣ 출력예제 1
2 : 3
3 : 1
4 : 1
5 : 2
6 : 2

전략

• 최단거리는 BFS
• 1번 정점에서 한 번만에 가는 정점들 찾기 + 두 번만에 가는 정점들 찾기.. => 큐 사용
  
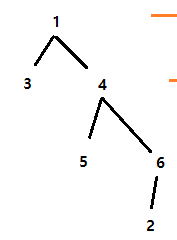
• 이미 방문한 정점은 다시 방문하지 않음
• 풀이 방법
  지금처럼 출발지점이 하나로 고정(1번정점)되어있을 경우 레벨 또는 dis 1차원 배열을 사용해 풀이 가능하나, 출발지점이 모든 정점이라면 dis 2차원 배열을 사용해 풀어야함 (12.토마토(BFS))

  방법1 : 기존처럼 거리를 레벨로 구하기
  
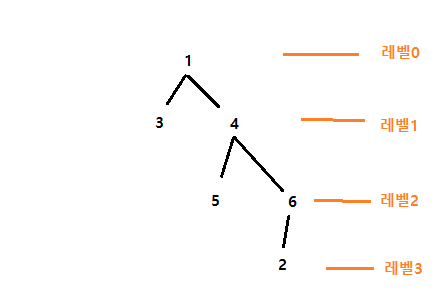
  방법2 : 거리를 dis배열을 사용하여 구하기
  (ex. dis[3] : 1번 정점에서 3번 정점까지 가는 최소 거리)
  
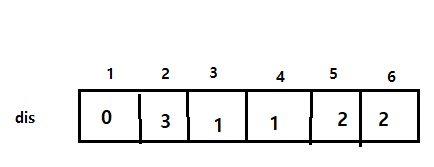
  dis[다음정점] = dis[현재정점]+1;

정답

방법2 사용

import java.util.*;
class Main {
    static int n, m, answer=0;
    static ArrayList<ArrayList<Integer>> graph;
    static int[] ch, dis;
    public void BFS(int v){
        ch[v]=1;
        dis[v]=0;
        Queue<Integer> queue=new LinkedList<>();
        queue.offer(v);
        while(!queue.isEmpty()){
            // cv : 현재 정점
            int cv=queue.poll();
            for(int nv : graph.get(cv)){
                // 방문 안한 정점만 방문
                if(ch[nv]==0){
                    ch[nv]=1;
                    queue.offer(nv);
                    dis[nv]=dis[cv]+1;
                }
            }
        }
    }

    public static void main(String[] args){
        Main T = new Main();
        Scanner kb = new Scanner(System.in);
        n=kb.nextInt();
        m=kb.nextInt();
        graph=new ArrayList<ArrayList<Integer>>();
        for(int i=0; i<=n; i++){
            graph.add(new ArrayList<Integer>());
        }
        ch=new int[n+1];
        dis=new int[n+1];
        for(int i=0; i<m; i++){
            int a=kb.nextInt();
            int b=kb.nextInt();
            graph.get(a).add(b);
        }
        // 출발지점은 1번 정점
        T.BFS(1);
        for(int i=2; i<=n; i++){
            System.out.println(i+" : "+dis[i]);
        }
    }
}