Q. 개념

---

1) 피보나키 수열을 출력한다. 피보나치 수열이란 앞의 2개의 수를 합하여 다음 숫자가 되는
수열이다.
2) 입력은 피보나치 수열의 총 항의 수 이다. 만약 7이 입력되면 1 1 2 3 5 8 13을 출력하면
된다.
▣ 입력설명
첫 줄에 총 항수 N(3<=N<=45)이 입력된다.
▣ 출력설명
첫 줄에 피보나치 수열을 출력합니다.
▣ 입력예제 1
10
▣ 출력예제 1
1 1 2 3 5 8 13 21 34 55

전략

• 피보나치수열은 재귀, for+Array 두가지 방식으로 푸는걸 코테에서 많이 물어본다.
  성능상으로는 for+Array방식이 좋다. 재귀는 수많은 정보(복귀주소 등)가 들어있는 스택프레임이 재귀함수가 호출 될 때 마다 쌓여서 메모리 낭비가 많이 일어나기 때문이다. 반면 for문은 해당 for문이 속한 함수 한번만 실행되므로 스택프레임도 한번만 생긴다.
• 구조

  [트리구조]
  DFS(n-2)+DFS(n-1); 로 인해 D(4)가 아니라 D(3)쪽이 먼저 호출된다.
  

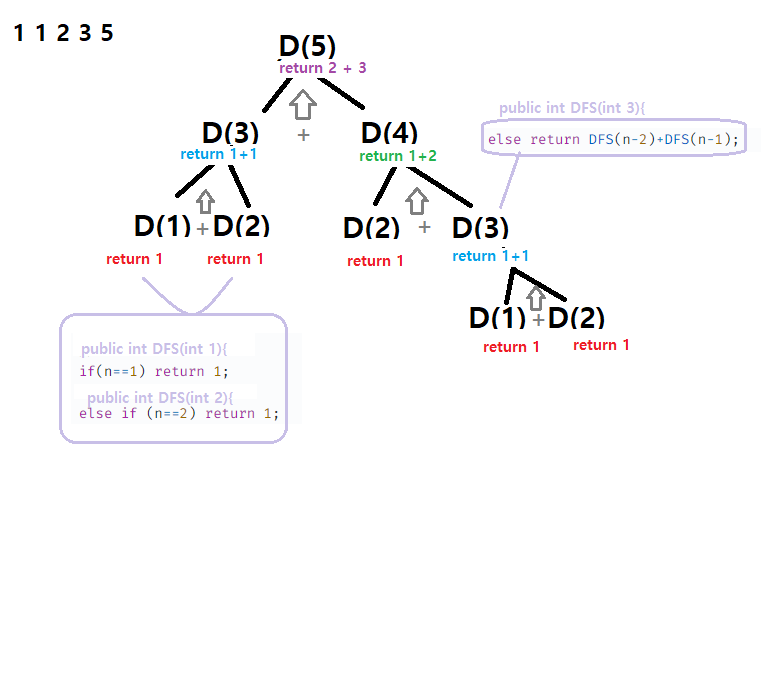
정답

출력방법 3 > 2 > 1 순으로 성능이 좋다.

• 출력방법 1 : 각 i 마다 재귀호출 -> 성능 비효율

import java.util.*;

class Main {
    static int[] fibo;

    // n번째 항의 값을 리턴받는다.
    public int DFS(int n){
        // 1번째 항일 때 1 리턴
        if(n==1) return 1;
        // 2번째 항일 때 1 리턴
        else if (n==2) return 1;
        // DFS(n-2)는 n-2번째 항의 값을 리턴받는다.
        // DFS(n-1)는 n-1번째 항의 값을 리턴받는다.
        else return DFS(n-2)+DFS(n-1);
    }
    public static void main(String[] args){
        Main T = new Main();
        int n=10;

        // 1 1 2 3 5 8 13 21 34 55에서 55를 리턴
//        System.out.println(T.DFS(n));

        // 출력방법 1
        for(int i=1; i<=n; i++){
            System.out.print(T.DFS(i)+" ");
        }


    }
}

• 출력방법 2 : D(n) 호출 시, 내부적으로 D(1)~D(n)까지 모두 호출된다. 내부적으로 호출 될 때 그 값을 배열에 기록해두어 출력시 배열을 순회하여 출력한다.
  (단, 이때 중복 호출 값은 배열에 다시 값이 기록된다)

import java.util.*;

class Main {
    static int[] fibo;

    // n번째 항의 값을 리턴받는다.
    public int DFS(int n){
        // 1번째 항일 때 1 리턴
        if(n==1) return fibo[n] = 1;
        // 2번째 항일 때 1 리턴
        else if (n==2) return fibo[n] = 1;
        // DFS(n-2)는 n-2번째 항의 값을 리턴받는다.
        // DFS(n-1)는 n-1번째 항의 값을 리턴받는다.
        // ex. n이 6인 경우, 4번째 항과 5번째 항의 합을 fibo[6]에 저장하고, 배열 fibo[6] 값을 리턴
        else return fibo[n] = DFS(n-2)+DFS(n-1);
    }
    public static void main(String[] args){
        Main T = new Main();
        int n=10;

        // 1 1 2 3 5 8 13 21 34 55에서 55를 리턴
//        System.out.println(T.DFS(n));

        // 출력방법 2
        // fibo[1]에 1번째 항 값을 기록하므로, n+1크기의 배열 필요 (배열 0번 인덱스 사용 X)
        fibo = new int[n+1];
        // 재귀호출은 한번만 한다 -> 출력방법 1보다 성능 효율
        T.DFS(n);
        for(int i=1; i<=n; i++){
            System.out.print(fibo[i]+" ");
        }
    }
}

• 출력방법 3(메모이제이션) : 내부적으로 중복 재귀 호출 되지 않게끔 기록된 배열값을 바로 꺼내 리턴한다.

import java.util.*;

class Main {
    static int[] fibo;

    public int DFS(int n){
        // 메모이제이션
        // 최초에 배열 원소들이 0으로 초기화되므로, 0보다 크다는건 값이 기록되어있다는 뜻
        // 값이 이미 기록되어있다면 DFS(n-2)+DFS(n-1);로 중복 재귀호출 할 필요없이 기록된 값 리턴
        if(fibo[n] > 0) return fibo[n];

        if(n==1) return fibo[n] = 1;
        else if (n==2) return fibo[n] = 1;
        else return fibo[n] = DFS(n-2)+DFS(n-1);
    }
    public static void main(String[] args){
        Main T = new Main();
        int n=10;

        fibo = new int[n+1];
        T.DFS(n);
        for(int i=1; i<=n; i++){
            System.out.print(fibo[i]+" ");
        }
    }
}