Q. 개념

---

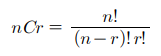로 계산합니다. 하지만 여러분은 이 공식을 쓰지않고 다음 공식을 사용하여
재귀를 이용해 조합수를 구해주는 프로그램을 작성하세요.

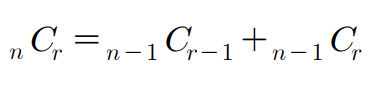
▣ 입력설명
첫째 줄에 자연수 n(3<=n<=33)과 r(0<=r<=n)이 입력됩니다.
▣ 출력설명
첫째 줄에 조합수를 출력합니다.
▣ 입력예제 1
5 3
▣ 출력예제 1
10
▣ 입력예제 2
33 19
▣ 출력예제 2
818809200

전략

• nCr : n개 중에서 r개를 뽑는 조합 개수

  순열과 조합은 다름.
  - 순열은 순서가 다르면 다른 경우의 수로 취급
  - 조합은 집합의 개념으로 순서가 달라도 원소가 같다면 하나의 경우의 수로 취급
  ex. {1,2,3,4,5}에서 3개를 뽑는 조합은 {1,2,3} "또는" {1,3,2}

• 다음 강의를 위한 배경지식 강의
• 참고 : 피보나치 강의

정답

import java.util.*;
class Main{
	// 메모이제이션 할 배열 선언
	// static인 main()에서는 접근 할 필요 없고 DFS()에서만 접근하면 되니까 static으로 선언 할 필요없음
	// n의 범위가 3<=n<=33, r의 범위가 0<=r<=n이므로 넉넉히 35로 잡는다.
	int[][] dy = new int[35][35];
	public int DFS(int n, int r){
		if(dy[n][r]>0) return dy[n][r];
		
		// n == r ex. 2C2인 경우, 2개 중 2개를 뽑는 경우의 수는 1
		// r == 0 ex. 2C0인 경우, 2개 중 0개를 뽑는 경우의 수는 1
 		if(n == r || r == 0) return 1;
		else return dy[n][r] = DFS(n-1, r-1) + DFS(n-1, r);
	}
	public static void main(String[] args){
		Main T = new Main();
		Scanner kb = new Scanner(System.in);
		int n = kb.nextInt(); 
		int r = kb.nextInt(); 
		System.out.println(T.DFS(n, r));
	}
}