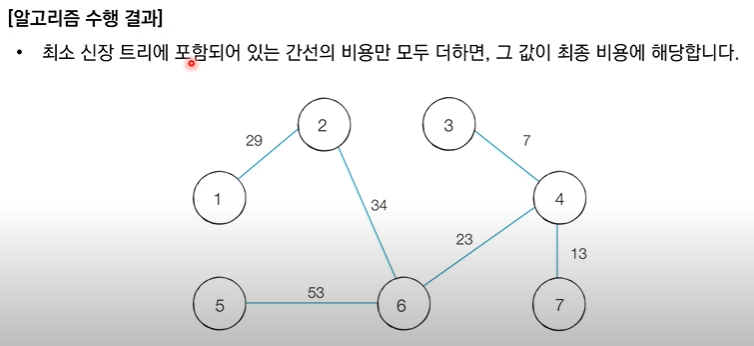
최소 신장 트리 알고리즘

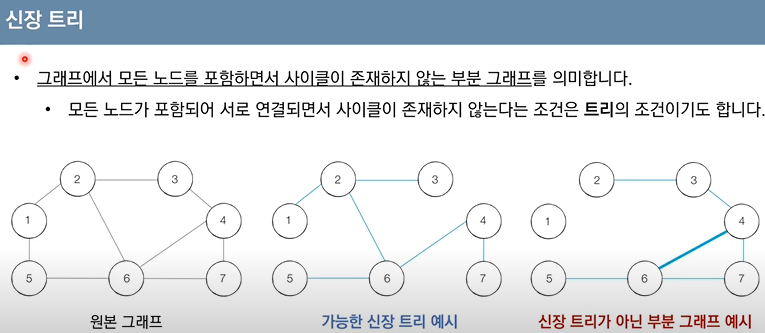✅ 일부 간선만을 채택한다는 특징
✅ 세번째 그래프는 모든 노드가 포함되어있지 않음 + 사이클 존재
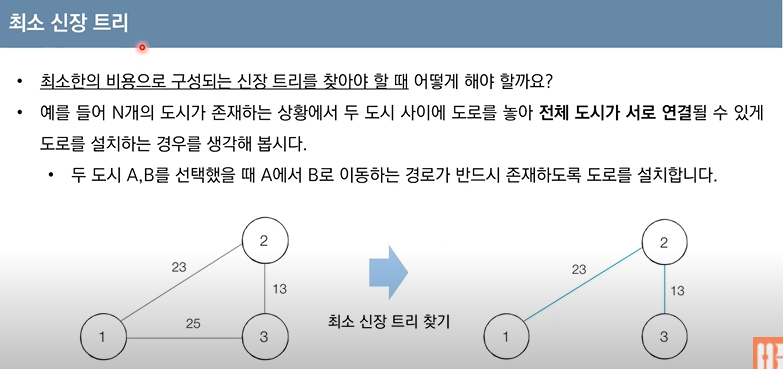✅ "반드시 존재하도록" : 신장트리는 모든 노드가 서로 연결되어있으므로 조금 돌아가더라더도 임의의 A,B가 서로 연결 되어있을 것이다.
✅ 최소 신장 트리의 간선 개수는 전체노드-1이다.

크루스칼 알고리즘

동작 원리

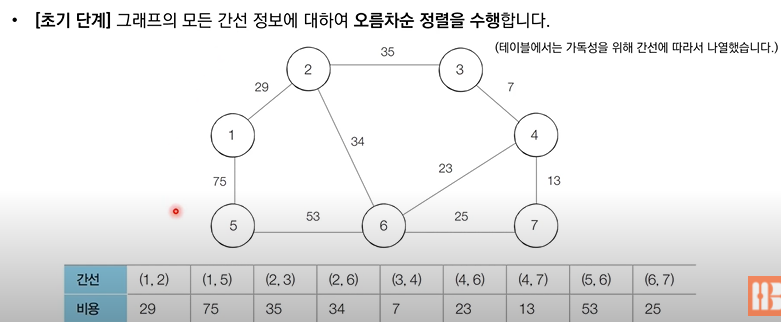
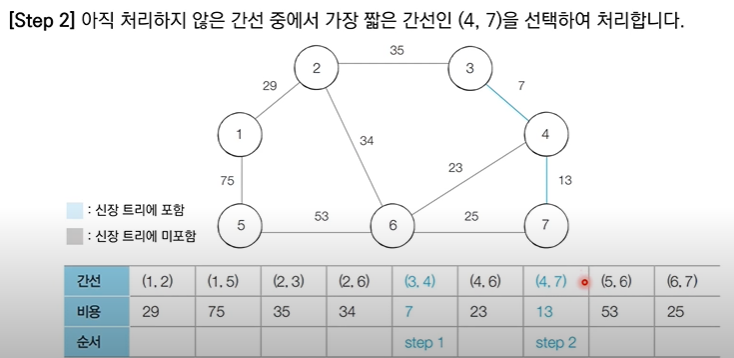
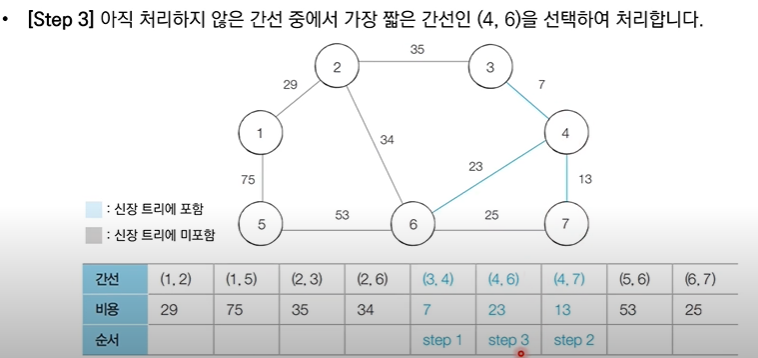
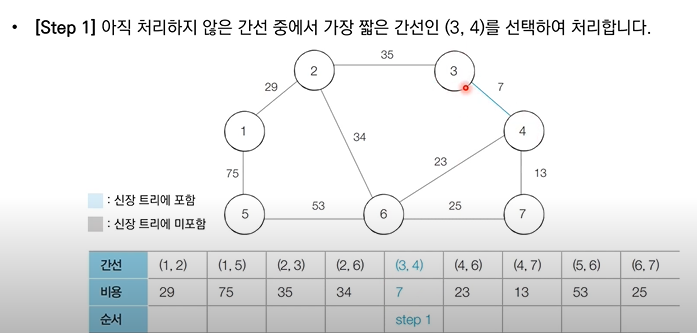✅ 3번 노드와 4번 노드는 같은 집합에 속해있지 않으므로 사이클이 발생하지 않을 것이기 때문에 같은 집합에 속하도록 union
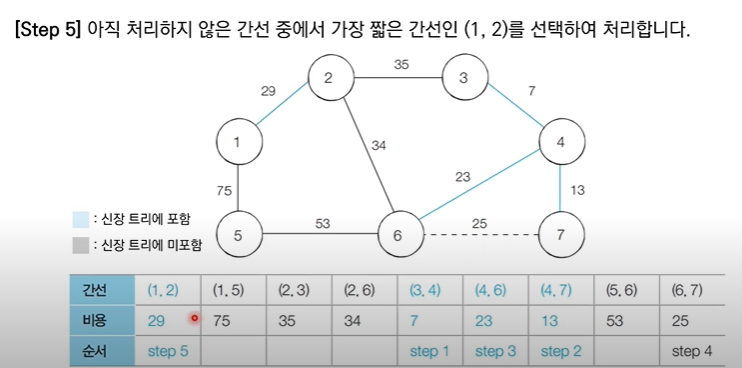
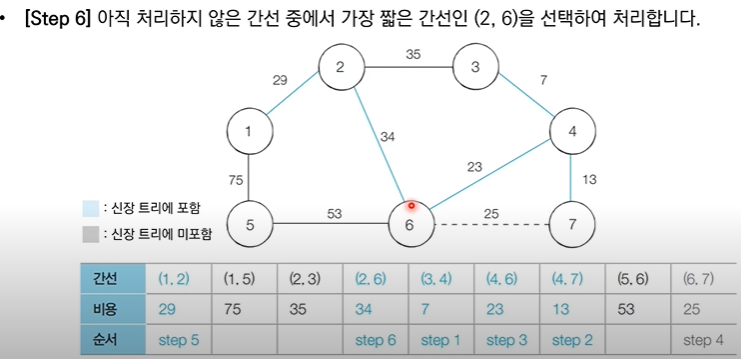
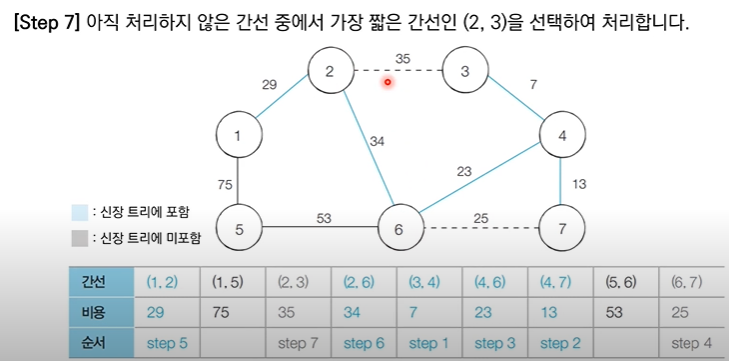
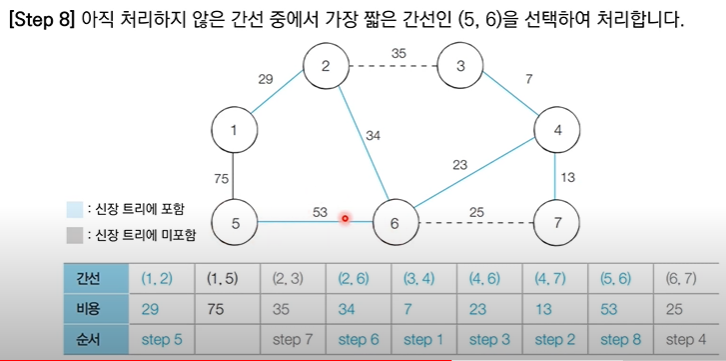
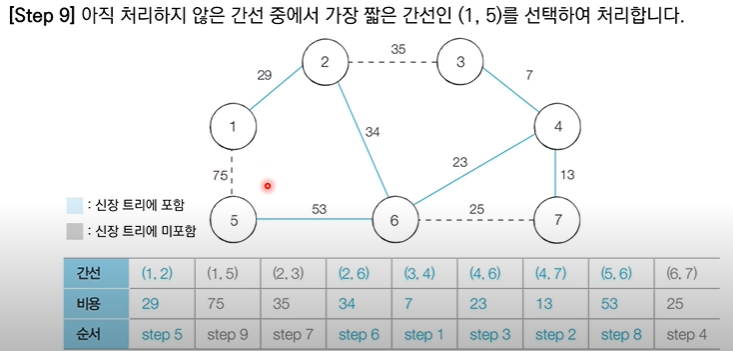
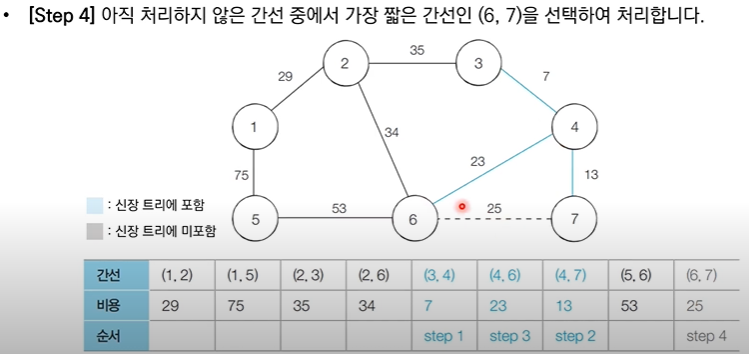✅ 6번 노드와 7번 노드는 같은 집합에 속해있기 때문에 사이클이 발생 할 것이므로 union X

소스

import java.util.*;

class Edge implements Comparable<Edge> {

    private int distance;
    private int nodeA;
    private int nodeB;

    public Edge(int distance, int nodeA, int nodeB) {
        this.distance = distance;
        this.nodeA = nodeA;
        this.nodeB = nodeB;
    }

    public int getDistance() {
        return this.distance;
    }

    public int getNodeA() {
        return this.nodeA;
    }

    public int getNodeB() {
        return this.nodeB;
    }

    // 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Edge other) {
        if (this.distance < other.distance) {
            return -1;
        }
        return 1;
    }
}

public class Main {

    public static int v, e;
    public static int[] parent = new int[100001];
    // 모든 간선을 담을 리스트
    public static ArrayList<Edge> edges = new ArrayList<>();
    // 최종 비용을 담을 변수
    public static int result = 0;

    public static int findParent(int x) {
        if (x == parent[x]) return x;
        return parent[x] = findParent(parent[x]);
    }

    public static void unionParent(int a, int b) {
        a = findParent(a);
        b = findParent(b);
        if (a < b) parent[b] = a;
        else parent[a] = b;
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        v = sc.nextInt();
        e = sc.nextInt();

        for (int i = 1; i <= v; i++) {
            parent[i] = i;
        }

        // 모든 간선에 대한 정보를 입력 받기
        for (int i = 0; i < e; i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int cost = sc.nextInt();
            edges.add(new Edge(cost, a, b));
        }

        // compareTo 기준으로 간선을 비용순으로 정렬
        Collections.sort(edges);

        // 간선을 하나씩 확인하며
        for (int i = 0; i < edges.size(); i++) {
            int cost = edges.get(i).getDistance();
            int a = edges.get(i).getNodeA();
            int b = edges.get(i).getNodeB();
            // 사이클이 발생하지 않는 경우에만 집합에 포함
            if (findParent(a) != findParent(b)) {
                unionParent(a, b);
                result += cost;
            }
        }

        System.out.println(result);
    }
}

성능 분석