[code][papers]Denoising diffusion probabilistic Models

박종훈·2023년 3월 20일

code&paper

목록 보기

1/1

이미지 생성 모델에서 milestone 이 되어주는 논문입니다.

이전에도 nonequilibrium thermodynamics 에서 영감을 받은 diffusion 계열 논문이 있었는데 높은 quality 의 이미지 생성 결과를 보여주면서 diffusion 계열 generation task 시대를 열었습니다.

필자가 생성한 실험 결과입니다.
실험 장비와 데이터 이슈로 실제 논문보다는 낮은 퀄리티의 이미지가 생성되네요.
코드 : https://github.com/suuperstone/SuuperCreator/tree/dev/ddpm

논문의 큰 방향

diffusion 모델의 기본 아이디어를 개괄적으로, 이해하기 쉬운 말로 표현하면 다음과 같습니다.

매우 작은 노이즈는 복구 가능하다

매우 작은 노이즈는 normal distribution sampling process 로 모델링 가능하다.

큰 노이즈는 매우 작은 노이즈의 중첩으로 모델링 가능하다.

큰 노이즈는, 매우 작은 노이즈에 대한 denoising 을 여러번 함으로써 제거 가능하다.

작은 노이즈의 복구 과정을, denoising 을 학습한 모델을 사용하는 방법론입니다.

노이즈의 모델링은 normal distribution sampling 으로 모델링이 가능하다고 했으니, 이제 고민해야 할 것이 몇가지 남습니다.

작은 노이즈의 중첩을 어떻게 모델링 할 것인가?

어떤 loss 를 사용해서 noise prediction을 학습시킬 수 있을까?

용어

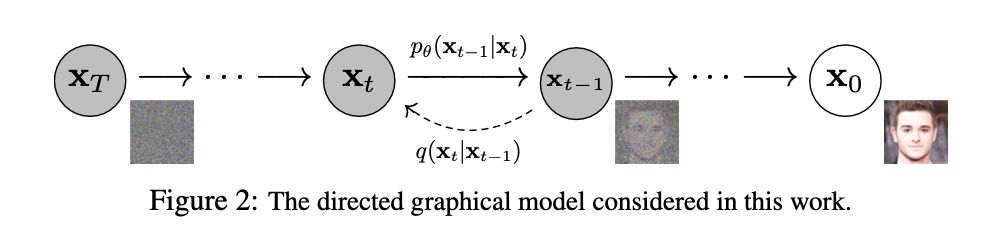
논문에서 반복적으로 사용되는 용어를 정리하면, 첫 정독에서 많은 도움이 됩니다.

$x_0$ : 최초의 이미지, 정상 이미지입니다.
$x_t$ : noising process 가 t 번 중첩된 이미지입니다.
$q_(x_{t}|x_{t-1})$ :
- forward process, diffusion process
- scheduled variance 값을 가지는 gaussian distribution 으로 모델링
$p(x_{t-1}|x_t)$ :
- 이상적인 $q_(x_{t}|x_{t-1})$ 의 reverse process 입니다.
$p_\theta(x_{t-1}|x_t)$ :
- $\theta$ 라는 parameter 로 parameterized 된 모델에 의해 생성되는 $q_(x_{t-1}|x_t)$ 의 reverse process, 즉 $p(x_{t-1}|x_t)$ 의 근사 process.

noise 중첩

매우 작은 variance 를 가지는 정규 분포의 곱은 정규 분포로 근사가능합니다. 논문에서는 $q(x_{t}|x_{t-1})$ 의 중첩인 $q(x_{t}|q_0)$ 를 단일 정규 분포로 근사합니다.

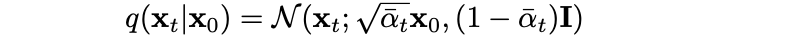
구현

    @torch.no_grad()
    def q_sample(self, x: torch.Tensor, t: torch.Tensor, noise=None):
        """
        forward process or diffusion process. add Guassian noise to input.
        Implementation of q(x_t|x_0).
        """
        if noise is None:
            noise = torch.randn_like(x)

        mean = self.alphas_cumprod.gather(-1, t).reshape(-1, 1, 1, 1)
        mean = mean.sqrt() * x
        var = 1 - self.alphas_cumprod.gather(-1, t).reshape(-1, 1, 1, 1)
        return mean + (var ** 0.5) * noise

loss 설정

DVAE 에서 제안된 negative log likelihood 를 loss 로 사용합니다.

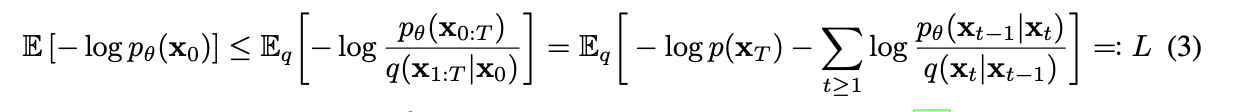
그 후 식을 전개하는데, 이 부분의 수식에 대해서는 많은 포스팅에서 설명하고 있어서 이 포스트에서는 수식 전개는 제외하겠습니다. 전개 자체는 식을 따라가면 그렇게 어렵지 않구요.

또, 전개를 하다보면 어 여기서 이미 loss 를 구할 수 있는 거 아닌가? 라는 지점이 있습니다. 다양한 reparmeterization 이 가능한데 논문에서는 noise prediction 이 가장 좋은 sample quality 를 보여준다고 주장합니다.

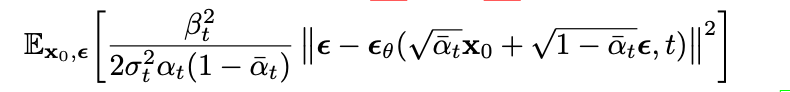
중요한 건, loss 의 upper bound 가 다음과 같은 수식으로 전개가 된다는 점이구...
절댓값 안의 값을 보면 특정 step 에서의 loss는 (실제 노이즈) - (노이즈가 있는 이미지, 현재 step 을 input 으로 model 의 output) 으로 계산 가능함을 알 수 있습니다.

또한, 절댓값 바깥의 변수 중 $\sigma_t = \beta_t$ 로 두는 게 실험적으로 더 좋은 퀄리티의 이미지를 생성했으며, 구현하기 단순하다는 이유로 구현에서는 무시합니다.

마지막으로 한가지 궁금한 점이 생깁니다.
위쪽에서 모델은 denoising process 의 근사 process 를 나타낸다고 했는데.. 왜 여기서는 noise 의 근사값을 계산하는 모델로 바뀌었나요?

A. 두 식이 모두 같은 의미를 가지며, denoising process 를 근사하는 모델을 나타내는 또 다른 방법이 수식 전개를 해보니 noise 를 근사하는 모델이였다, 라고 이해하면 됩니다.

Training

논문을 이 정도 읽으면 복잡했던 지금까지의 수식들이 마법처럼 단순한 loss bound 로 계산되는 simple training algorithm 으로 완성됩니다.

training process 의 의미는,
원본 이미지 $x_0$ 가 주어졌을 때 random step $t$ 에서 noise 를 예측하는 모델을 생성하는 과정입니다.

Random step 생성

해당 step 에서 noise 생성 및 input image 에 추가

noise 값 예측 ( model)

loss 계산 - 아래 구현에서는 간단한 mse-loss 사용

구현

    def forward(self, img):
        """
        Training Process.
        Implementation of `Algorithm1. Training`
        x : B x C x H x W
        """
        # image data scaled linearlly to [-1, 1] in ddpm.
        img = scale_img_linear(img)

        b, c, h, w = img.size()
        # t ~ Uniform({1,...,T}), noise ~ normal(0, I)
        # if t is 0, the diffused image is original image.
        # if t is 1, the diffused image is assumed to be noiseless at the end of sampling.
        t = torch.randint(0, self.num_timesteps, (b,), device = img.device).long()
        noise = torch.randn_like(img)

        x = self.q_sample(img, t, noise=noise)
        model_out = self.model(x, t)

        loss = self.loss_fn(model_out, noise, reduction = 'none')
        loss = self.p2_loss_weight.gather(-1, t).view(b,1,1,1) * loss

        return loss.mean()

Sampling

단연히, noise 를 예측하는 모델을 생성했으니 이제 Denoising 이 가능합니다. 주어진 diffuion step $t$ 에서 부터 $0$ 까지 한 단계씩 denoising 을 해나가는 과정이겠네요.

이 개념을 담은 개괄적인 코드는 아래와 같습니다

구현

    @torch.no_grad()
    def sample(self, n_samples, img_channels, img_size, noise_clamp=False, denoised_clamp=False):
        """
        Implementation of `Algorithm2. Sampling`
        """
        x = torch.randn([n_samples, img_channels, img_size, img_size], device=self.betas.device)
        for _, t_ in tqdm(enumerate(range(self.num_timesteps))):
            t = self.num_timesteps - t_ - 1
            x = self.p_sample(x, x.new_full((n_samples,), t, dtype=torch.long),
                              noise_clamp=noise_clamp,
                              denoised_clamp=denoised_clamp)
        x = unscale_img_linear(x.clamp(min=-1, max=1))

조금 식을 봅시다, 우리는 에러를 예측하는 모델을 만들었는데 그냥 모델 output 을 계속해서 빼주면 denoising 이 맞지 않나?

Sampling 의 개념이라서 조금 달라지게 되는데,
먼저 저희가 예측한 noise 는 실제 reverse process 의 근사 분포로 부터 sampling 한 값이라고 봐도 무방합니다. 그러므로 sampling 을 하기 위해서 생성된 근사값으로부터... 실제 reverse process 의 평균( $t+1$ 시점의 이미지) 과 분산을 추정해야겠죠. 그런데 평균은 아니까, 저희는 분산의 추정값을 구하고 이로부터 실제 $t$ 시점에서의 가능한 $x_t$ 의 분포 근사로부터 이미지를 샘플링할 수 있게 됩니다.