백준 1932

문제

---

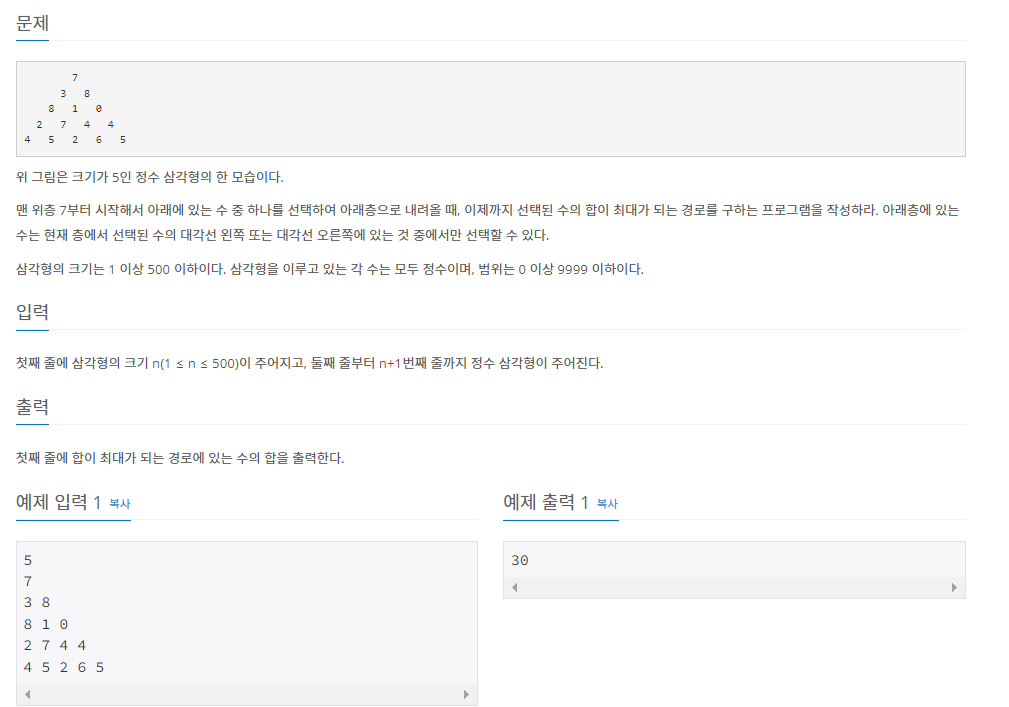
위에서 부터 최대 합을 탐색하는 것이 아닌....

아래쪽부터 탐색하는 것이 훨씬 빠르다.

예를 들어 문제의 예시에 나온 삼각형의 왼쪽 하단

2
4 5

를 보자. 만약 이 숫자들 중 2개가 최대합에 포함된다면?

당연히 2+ 4 보다 2 + 5 가 크니까 2와 5가 포함될 것이다.

다음으로

8
2 7
4 5 2

를 보면,

8로 가기 직전의 경로 중 최대합은 2개 있다.

5 + 2 = 7(2를 지나는 경로) 과 5 + 7 = 12(7을 지나는 경로)

따라서 최대합의 후보는 5 + 2 + 8 과 5 + 7 + 8 인데

당연히 합이 최대인 경로는 이미 직전 깊이에서 값이 더 큰 5 + 7 = 12 쪽 경로 일 것이다.

dp에는

20
7 12
4 5 2

과 같이 최하단 깊이부터 탐색해서 각 요소까지 왔을 때 가장 큰 합을 저장한다.

dp[i][j] : 최하단 깊이부터 탐색해서 맨 아래에서 i 번째 깊이의 j번째 요소까지 경로 중 최대 합

즉, 가장 아래에서 탐색하되, 각 요소의 2개의 경로(의 합) 중 어느 것을 부모 요소에 더해야 최대 합이 나올지 파악한다. 이 작업 최상단 요소까지 반복!

---

Code

package test;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;



public class P1932 {
	private static int n;
	private static int[][] triangle;
	
	// dp[i][j] : 맨 아래에서 i 번째 깊이의 j번째 요소까지 경로 중 최대 합
	private static Integer[][] dp;
	
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		n = Integer.parseInt(br.readLine());
		triangle = new int[n][n];
		dp = new Integer[n][n];
		StringTokenizer st;
		for(int i = 0; i < n; i++) {
			st = new StringTokenizer(br.readLine(), " ");
			
			for(int j = 0; j <= i; j++) {
				triangle[i][j] = Integer.parseInt(st.nextToken());
			}
		}
		
		// dp의 맨 아래 값들은 합을 구하지 전이므로 삼각형의 맨 아래 값들과 같다.
		for(int i = 0; i < n; i++) {
			dp[n - 1][i] = triangle[n - 1][i];
		}
		
		System.out.println(find_maxSum(0, 0));
		
	}
	
	private static int find_maxSum(int depth, int idx) {
		if(depth == n - 1) {
			return dp[depth][idx];
		}
		if(dp[depth][idx] == null) {
			
			dp[depth][idx] = 
					Math.max(
							find_maxSum(depth + 1, idx), find_maxSum(depth + 1, idx + 1)
							)
					+ triangle[depth][idx];
		}
		return dp[depth][idx];
	}

}

---

참고 : https://st-lab.tistory.com/131