비지도 학습의 큰 주제

• 군집
• 이상치 탐지
• 밀도 추정

9.1 군집

Clustering (군집화): 비슷한 샘플을 하나의 Cluster 또는 비슷한 샘플의 그룹으로 할당하는 작업

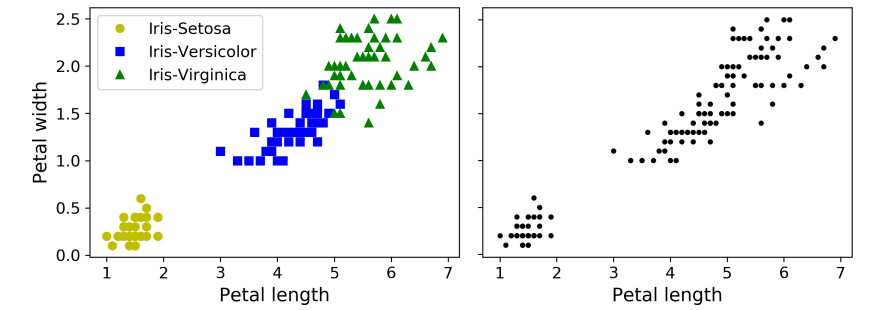
위 그림은 붖꽃 데이터셋이다.

• 왼쪽 데이터셋은 레이블이 있지만, 오른쪽 데이터셋은 레이블이 없음.
• 레이블이 없는 데이터셋은 분류와 같은 지도 학습 알고리즘을 적용할 수 없음.

군집이 사용되는 다양한 어플리케이션?

• 고객 분류
• 데이터 분석
• 차원 축소 기법
• 이상치 탐지
• 준지도 학습
• 검색 엔진
• 이미지 분할

9.1.1 K-Means

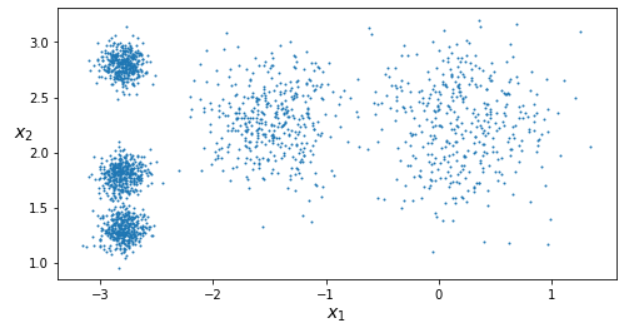
위 그림과 같은 샘플에 대하여 k-means 알고리즘 학습

from sklearn.cluster import KMeans
k = 5
kmenas = KMeans(n_clusters = k)
y_pred = kmeans.fit_predict(X) #이때 X는 2차원 좌표 값들

• 위의 코드에서는 각 샘플은 다섯 개의 클러스터 중 하나에 할당.
• 군집에서 각 샘플의 레이블은 알고리즘이 샘플에 할당한 클러스터의 인덱스 (클러스터 번호)
• KMeans 클래스의 인스턴스는 labels_ 인스턴스 변수에 훈련된 샘플의 레이블을 지님.

kmeans.cluster_centers_ 

• 코드 cluster_centers_로 센트로이드 (클러스터의 중심)를 찾을 수 있음.

X_new = np.array([[0,2], [3,2], [-3,3], [-3,2.5]])
kmeans.predict(X_new)

• 또한 새로운 샘플에 대하여 가장 가까운 센트로이드의 클러스터를 할당할 수 있음.
  
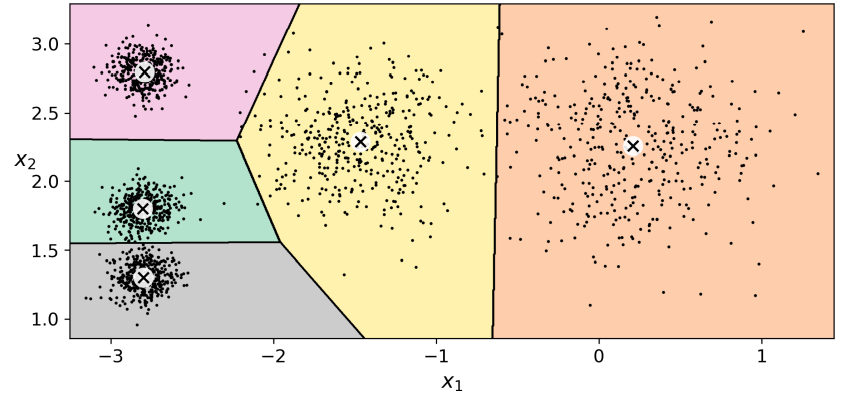
  클러스터의 결정 경계를 그려서 보로노 다이어그램을 얻은 그림.
• 센트로이드는 x로 표시됨.
• 몇몇 샘플은 레이블이 잘못 부여되었음. (특히 왼쪽 위에 있는 클러스터돠 가운데 클러스터의 경계 부근)
• 실제 k-Means 알고리즘은 클러스터의 크기(클러스터의 지름)가 많이 다르면 잘 작동하지 않음.
• 샘플을 클러스터에 할당할 때 센트로이드까지 거리를 고려하는 것이 전부이기 때문.

Hard Clustering

• 샘플을 하나의 클러스터에 할당하는 것

Soft Clustering

• 클러스터마다 샘플에 점수를 부여하는 것
  ex) 이 점수는 샘플과 센트로이드 사이의 거리가 될 수 있음. 이때 KMeans 클래스의 transform() 메서드는 샘플과 각 센트로이드 사이의 거리를 반환함.

K-Means 기본적인 알고리즘 작동 방식

1) 랜덤으로 중심(센트로이드)을 할당
2) 모든 샘플들에 대하여 모든 센트로이드와의 거리를 계산하여 가장 거리가 짧은 클러스터로 할당
3) 각 센트로이드의 클러스터의 중심을 업데이트 (샘플들의 중심점으로)
4) 센트로이드에 변화가 없을 때까지 계속 반복

센트로이드의 init 설정하는 3가지 방법

• 모델의 이너셔 (inertia): 각 샘플과 가장 가까운 센트로이드 사이의 평균 제곱거리
  1) 랜덤하게 설정 -> 여러번 알고리즘 실행, 가장 좋은 솔루션 선택
  2) 원래 고정되어있는 센트로이드의 위치를 근사적으로 알 때
  3) K-Means++ 방법 (sklearn의 KMeans는 기본적으로 이를 사용함)

K-Means++ 알고리즘 설명

1) 데이터셋에서 무작위로 균등하게 하나의 센트로이드 $c^{(1)}$ 선택
2) $(D(x^{(i)}))^2/\sum_{j=1}^m (D(x^{(j)}))^2$의 확률로 샘플 $x^{(i)}$를 새로운 센트로이드 $c^{(i)}$로 선택함.

• 이 수식에서 $D(x^{(i)})$는 샘플 $x^{(i)}$과 가장 가까운 센트로이드 ($c^{(1)}$ ~ $c^{(i-1)}$ 중에 가장 가까운 거리)를 의미한다.
• 즉 이 확률 분포는 이미 선택한 센트로이드에서 멀리 떨어진 샘플을 다음 센트로이드로 선택할 가능성을 높이게 된다.
  3) k개의 센트로이드가 선택될 때까지 이전 단계를 반복

k-Means 속도 개선과 미니배치 k-Means

• 속도는 더 빨라질 것

from sklearn.cluster import MiniBatchKMeans

minibatch_kmeans = MiniBatchKMeans(n_clusters = 5)
minibatch_kmeans.fit(X)

• 만약 데이터셋이 메모리에 들어가지 않으면 가장 간단한 방법은 8장의 점진적 PCA에서 했던 것처럼 memmap 클래스를 사용하는 것.
• 또는 MiniBatchKMeans 클래스의 partial_fit() 메서드에 한 번에 하나의 미니배치를 전달할 수 있음.
• 하지만 초기화를 여러 번 수행하고 만들어진 결과에서 가장 좋은 것을 직접 골라야 해서 해야 할 일이 많다.
• 미니배치가 일반 k-means보다 빠르긴 하지만 이너셔, inertia는 일반적으로 더 나쁨.

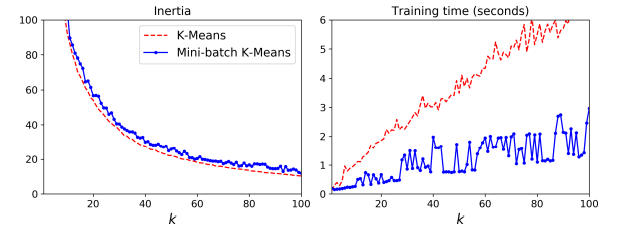
• 왼쪽 그림에서 미니배치 k-means가 이너셔 값이 더 안 좋다는 것을 확인할 수 있음.
• 오른쪽 그림에서 훈련 시간은 미니배치 k-meams가 더 짧게 걸림.

최적의 클러스터 개수 찾기

• 무작정 k 값을 늘린다고 좋은 것이 아님.
• 클러스터의 개수를 늘리면 자연히 이너셔의 값은 줄어들 수 밖에 없음.
  
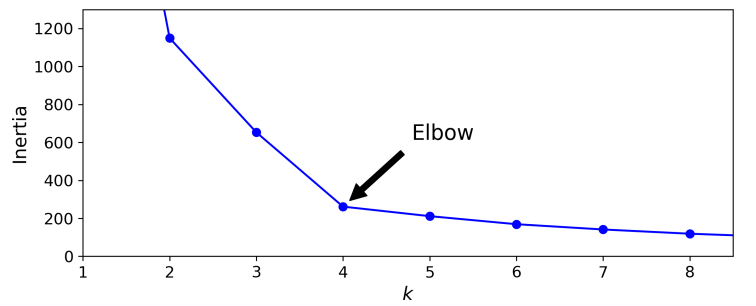
• 만약 K의 값을 모른다면 Elbow라 불리는 지점에서 클러스터를 구성하는게 좋은 선택이 될 것 같음.

-> 하지만 이 방법은 너무 엉성한 방법임. -> 더 정확한 (하지만 Cost가 더 드는) 방법은 '실루엣 점수'임

실루엣 점수: 모든 샘플에 대한 실루엣 계수의 평균

• 실루엣 계수: (b-a)/max(a, b)로 계산
• a: 동일한 클러스터에 있는 다른 샘플까지 평균 거리
  - (즉 클러스터 내부의 평균 거리)
• b: 가장 가까운 클러스터까지 평균 거리
  - (즉 가장 가까운 클러스터의 샘플까지 평균 거리. 샘플과 가장 가까운 클러스터는 자신이 속한 클러스터는 제외하고 b가 최소인 클러스터)
• 실루엣 계수는 -1 ~ +1 까지 바뀔 수 잇음.
• +1에 가까우면 자신의 클러스터 안에 잘 속해 있고, 다른 클러스터와 멀리 떨어져 있다는 뜻.
• 실루엣 계수가 0에 가까우면 클러스터 경계에 위치
• -1에 가까우면 이 샘플이 잘못된 클러스터에 할당되었다는 의미
• 실루엣 점수는 나이킷런의 silhouette_score() 함수를 사용. ->샘플과 할당된 레이블을 전달

from sklearn.metrics import silhouette_score
silhouette_score(X, kmeans.labels_)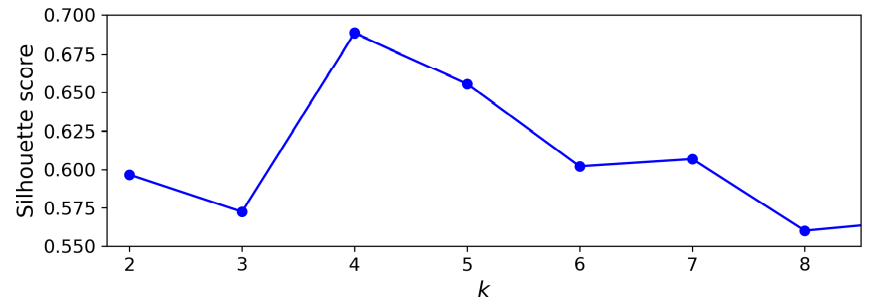

• 실루엣 점수는 k=4일 때 최대이지만, k=5도 꽤 좋다는 사실을 보여줌.

실루엣 다이어그램

• 모든 샘플의 실루엣 계수를 할당된 클러스터와 계숫값으로 정렬하여 그린 그래프
• 높이: 클러스터가 포함하고 있는 샘플의 개수
• 너비: 클러스터에 포함된 샘플의 정렬된 실루엣 계수
• 넓을 수록 좋은 값.

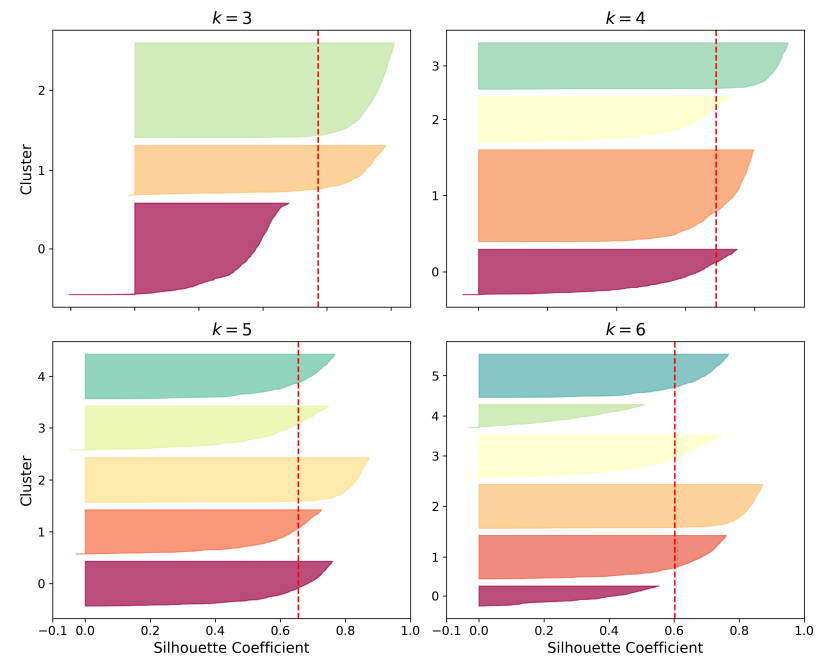
• 수직 파선: 각 클러스터 개수에 해당하는 실루엣 점수를 나타냄
• 한 클러스터의 샘플 대부분이 이 점수보다 낮은 계수를 가지면 (즉 많은 샘플이 파선의 왼쪽에서 멈추면) 클러스터의 샘플이 다른 클러스터랑 너무 가깝다는 것을 의미. (나쁜 클러스터)
• k=4일 때보다 k=5 일대 대부분의 샘플의 크기가 비슷하다.

9.1.2 K-Means의 한계

• 클러스터의 크기나 밀집도가 서로 다르거나, 원형(circular)이 아닐 경우 잘 작동하지 않음.
  
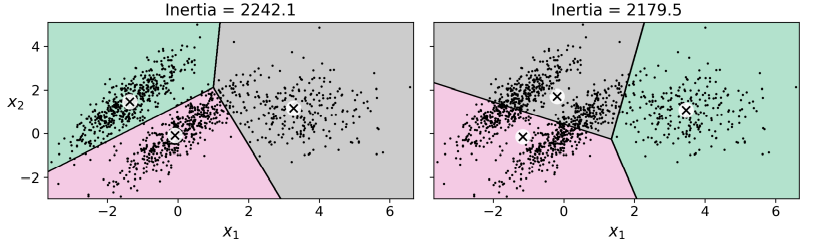
  이런 타원형 클러스터링은 가우시안 혼합 모델이 잘 작동.

9.1.6 DBSCAN

DBSCAN: Density Based spatial clustering of applications with noise-> 밀도 기반 클러스터링

• 밀집된 연속적 지역을 클러스터로 정의

  DBSCAN 작동 방식

  1) 알고리즘이 각 샘플에서 작은 거리인 ε(하이퍼 파라미터) 내에 샘플이 몇 개 놓여 있는지 센다. 이 지역을 샘플의 ε-이웃 (neighborhood)이라고 부릅니다.
  2) (자기 자신을 포함해) ε-이웃 내에 적어도 min_samples (하이퍼 파라미터)개의 샘플이 있다면 이를 핵심 샘플(core instance)로 간주합니다. 즉 핵심 샘플은 밀집된 지역에 있는 샘플입니다.
  3) 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터에 속합니다. 이웃에는 다른 핵심 샘플이 포함될 수 있습니다. 따라서 핵심 샘플의 이웃의 이웃은 계속해서 하나의 클러스터를 형성합니다.
  4) 핵심 샘플이 아니고 이웃도 아닌 샘플은 이상치로 판단합니다.

이 알고리즘은 모든 클러스터가 충분히 밀집되어 있고 밀집되지 않은 지역과 잘 구분될 때 좋은 성능을 냅니다.

• 사이킷런에 있는 DBSCAN 클래스를 사용하면 된다.

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=1000, noise=0.05)
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbsacn.fit(X)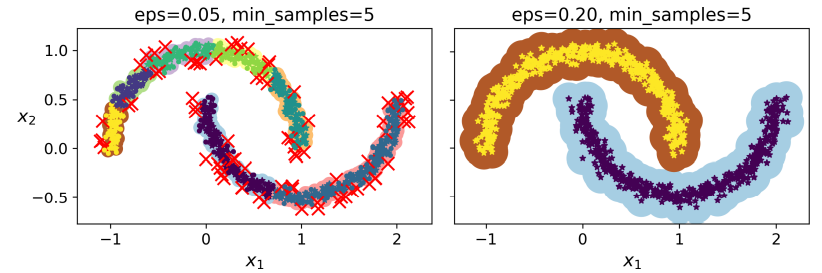

입실론 값에 따른 군집의 결과입니다.

• 핵심 샘플의 인덱스는 인스턴스 변수 coresample_indices에서 확인할 수 있음.
• 핵심 샘플 자체는 인스턴스 변수 components_에 저장되어있음.

장점

• K-Means와 같이 클러스터의 수를 정하지 않아도 된다.
• 클러스터의 밀도에 따라 클러스터를 연결하기 때문에 복잡한 기하하학적 모양을 갖는 군집도 잘 찾을 수 있다.
• Noise Point를 통하여 outlier 검출이 가능하다.

sklearn에서 제공하는 DBSCAN 클래스는 predict() 메서드를 제공하지 않고, fit_predict() 메서드를 제공합니다.

• 이는 새로운 샘플에 대해 클러스터를 예측할 수 없습니다. 이런 구현 결정은 다른 분류 알고리즘이 이런 작업을 더 잘 수행할 수 있기 때문입니다.
• 따라서 사용자가 필요한 예측기를 선택해야 합니다. 또 구현하는 것이 어렵지도 않습니다.
• 예를 들어 KNeighborClassifier 훈련

from sklearn.neighbors import KNeighborClassifier

knn = KNeighborClassifier(n_neihbors = 50)
knn.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])

X_new = ap.array([[-0.5, 0], [0,0.5], [2,1]])
print(knn.predict(X_new))
print(knn.predict_proba(X_new))

kneigbors 메서드에 샘플을 전달하면 훈련 세트에서 가장 가까운 k개의 이웃의 거리와 인덱스를 반환함. (k개 열을 가진 행렬 두개를 반환)

>>> y_dist, y_pred_idx = knn.kneighbors(X_new, n_neighbors=1)
>>> y_pred = dbscan.labels_[dbscan.core_sample_indices_][y_pred_idx]
>>> y_pred[y_dist > 0.2] = -1
>>> y_pred.ravel()
array([-1, 0, 1, -1])

9.2 가우시안 혼합 모델 (Gassian Mixture Model)

가우시한 혼합 모델, GMM

• 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 가우시안 분포에서 생성되었다고 가정하는 확률 모델.
• 하나의 가우시안 분포에서 생성된 샘플은 하나의 클러스터를 형성.
• 일반적으로 타원형의 클러스터.
• 각 클러스터는 아래 그림처럼 타원의 모양, 크기, 밀집도, 방향이 다름.
  

GMM은 사전에 가우시안 분포의 개수 k를 알아야 함.

데이터셋 $X$가 다음 확률 과정을 통해 생성되었다고 가정함.

• 샘플마다 $k$개의 클러스터에서 랜덤하게 한 클러스터가 선택됩니다. $j$번째 클러스터를 선택할 확률은 클러스터의 가중치 $\phi^{(j)}$로 정의됩니다. $i$번째 샘플을 위해 선택한 클러스터 인덱스는 $z^{(i)}$로 표시합니다.
• $z^{(i)} = j$이면, 즉 $i$번째 샘플이 $j$번째 클러스터에 할당되었다면 이 샘플의 위치 $x^{(i)}$는 평균이 $\mu^{(j)}$, 공분산 행렬이 $\sum^{(j)}$인 가우시안 분포에서 랜덤하게 샘플링 됩니다.
  이를 $x^{(i)}$ ~ $N(\mu^{(j)}, \sum^{(j)})$라고 씁니다.

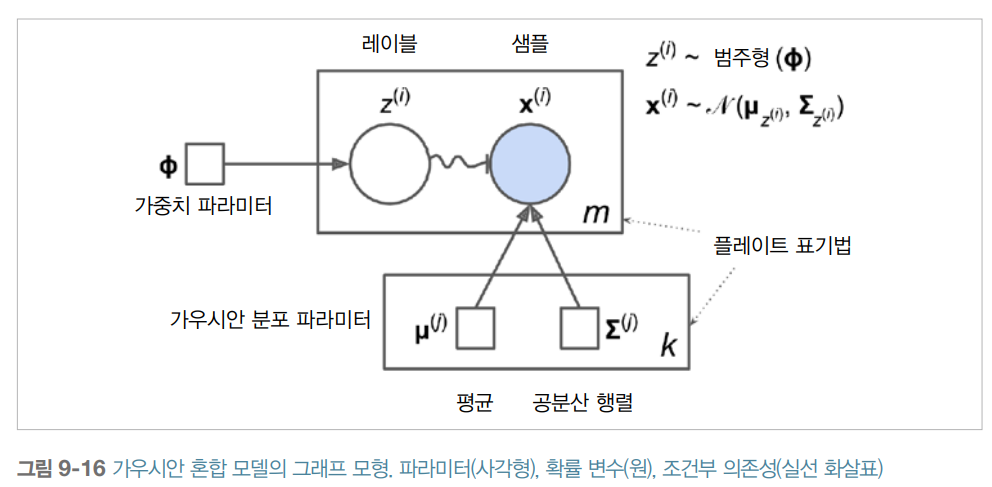
이 생성과정은 그래프 모형으로 나타낼 수 있음. 아래의 그림은 확률 변수 사이의 조건부 의존성의 구조를 나타냄.

위 그림을 보는 방법은 아래와 같음.

• 원은 확률 변수를 나타냄.
• 사각형은 고정값을 나타냄. (즉 모델의 파라미터를 나타냄.)
• 큰 사각형을 플레이트(plate)라고 부름. 이 사각형 안의 내용이 여러 번 반복된다는 것을 나타냄.
• 각 플레이트 오른쪽 아래의 숫자는 얼마나 플레이트 안의 내용이 반복되는지를 표시함. 따라서 m개의 확률 변수 $z^{(i)}$ ($z^{(1)}$ ~ $z^{(m)}$)와 m개의 확률 변수 $x^{(i)}$가 있음. 또한 k개의 가우시안 분포의 평균 $\mu^{(j)}$와 k개의 공분산 행렬 $\sum^{(j)}$이 있음. 마지막으로 하나의 가중치 벡터 $\phi$ 가 있습니다. (가중치 $\phi^{(1)}$ 부터 $\phi^{(k)}$까지 포함한 벡터임.)
• 각 변수 $z^{(i)}$는 가중치 $\phi$를 갖는 범주형 분포에서 샘플링합니다. 각 변수 $x^{(i)}$는 해당하는 클러스터 $z^{(i)}$로 정의된 평균과 공분산 행렬을 사용해 정규분포에서 샘플링합니다.
• 실선 화살표는 조건부 의존성을 표현합니다. 예를 들어 각 확률 변수 $z^{(i)}$의 확률 분포는 가중치 벡터 $ϕ$에 의존합니다. 화살표가 플레이트 경계를 가로지르면 해당 플레이트의 모든 반복에 적용한다는 의미입니다. 예를 들어 가중치 벡터 $ϕ$는 확률 변수 $x^{(1)}$ 에서 $x^{(m)}$까지 모든 확률 변수의 확률 분포에 필요 조건입니다.
• $z^{(i)}$에서 $x^{(i)}$까지 구불구불한 화살표는 스위치를 나타냅니다. $z^{(i)}$의 값에 따라 샘플 $x^{(i)}$가 다른 가우시안 분포에서 샘플링될 것입니다. 예를 들어 $z^{(i)}=j$이면 $x^{(i)}$ ~ $N(\mu^{(j)}, \sum^{(j)})$가 됩니다.
• 색이 채워진 원은 알려진 값이라는 의미입니다. 따라서 이 경우에 확률 변수 $x^{(i)}$만 알고 있는 값입니다. 이를 관측 변수라고 합니다. 알려지지 않은 확률 변수 $z^{(i)}$를 잠재 변수라고 부릅니다.

• 사이킷런의 GaussianMixture 클래스를 이용하면 데이터셋 $X$가 주어졌을 때 가중치 $\phi$와 전체 분포의 파라미터 $\mu^{(1)}$부터 $\mu^{(k)}$, $\sum^{(1)}$에서 $\sum^{(k)}$까지 추정할 수 있습니다.

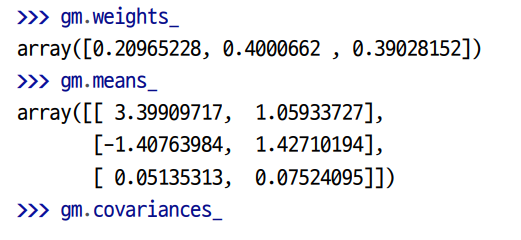
• 알고리즘이 추정한 파라미터들을 확인할 수 있습니다.