[JAVA] 다익스트라

다익스트라란?

• 다익스트라 알고리즘은 최단 경로(Shortest Path) 탐색 알고리즘이다.
• 입력 그래프는 양수의 가중치 그래프이다.
  • BFS 알고리즘은 가중치가 1인 그래프에만 적용되지만 다익스트라는 1보다 커도 된다.
• 프림(Prim)의 MST 알고리즘과 흡사한 과정으로 진행된다.
  • 차이점
    • Prim 알고리즘은 임의의 점에서 시작하지만, 다익스트라 알고리즘은 주어진 출발점에서 시작한다.
    • Prim 알고리즘은 트리에 하나의 점(선분)을 추가시킬 때 현재 상태의 트리에서 가장 가까운 점을 추가한다.
    • 다익스트라 알고리즘은 출발점으로부터 최단 거리가 확정되지 않은 점들 중에서 출발점으로부터 가장 가까운 점을 추가하고, 그 점의 최단 거리를 확정한다.
• 우선순위 큐(Priority Queue)를 사용하여 시간 복잡도를 단축시킬 수 있다.

다익스트라 진행 과정

입력 : 가중치 그래프 $G=(V, E)$, $|V|=n$(점의 수), $|E|=m$(선분의 수)
출력 : 출발점 s로부터 (n - 1)개의 점까지 각각 최단 거리를 저장한 배열 D
1. 배열 D를 $\infty$로 초기화 시킨다. 단, $D[s]=0$으로 초기화 한다.
2. while (s로부터 최단 거리가 확정되지 않은 점이 있으면) {
현재까지 s로부터 최단 거리가 확정되지 않은 각 점 v에 대해서 최소의 $D[v]$의 값을 가진 점 $v_{min}$을 선택하고, 출발점 s로부터 점 $v_{min}$까지의 최단 거리 $D[v_{min}]$을 확정시킨다.
s로부터 현재보다 짧은 거리로 점 $v_{min}$을 통해 우회 가능한 각 점 w에 대해서 $D[w]$를 갱신한다.
}
return D

코드

• Priority Queue 미사용

import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;

public class Dijkstra {

    static final int INF = 9999999;

    static class Node implements Comparable<Node>{
        int to, w;

        public Node(int to, int w) {
            this.to = to;
            this.w = w;
        }

        @Override
        public int compareTo(Node o) {
            return this.w - o.w;
        }
    }

    public static void main(String[] args) {
        int V = 5;  // 정점의 수
        int E = 6;  // 간선의 수

        // 인접리스트 선언 및 초기화
        ArrayList<ArrayList<Node>> adjList = new ArrayList<>();
        for (int i = 0; i <= V; i++) {
            adjList.add(new ArrayList<>());
        }

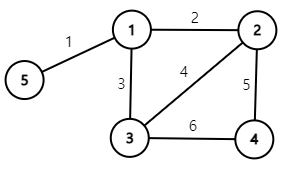
        // 인접리스트 입력
        adjList.get(5).add(new Node(1, 1));
        adjList.get(1).add(new Node(5, 1));

        adjList.get(1).add(new Node(2, 2));
        adjList.get(2).add(new Node(1, 2));

        adjList.get(1).add(new Node(3, 3));
        adjList.get(3).add(new Node(1, 3));

        adjList.get(2).add(new Node(3, 4));
        adjList.get(3).add(new Node(2, 4));

        adjList.get(2).add(new Node(4, 5));
        adjList.get(4).add(new Node(2, 5));

        adjList.get(3).add(new Node(4, 6));
        adjList.get(4).add(new Node(3, 6));

        // 시작 정점
        int st = 1;

        int[] dist = new int[V + 1];           // 최소거리 배열
        Arrays.fill(dist, INF);                // 무한대로 초기화
        dist[st] = 0;                          // 시작 정점은 0으로
        boolean[] visit = new boolean[V + 1];  // 방문 체크 배열

        for (int i = 1; i <= V; i++) {
            int nodeValue = Integer.MAX_VALUE;
            int nodeIdx = 0;
            for (int j = 1; j < V + 1; j++) {
                if (!visit[j] && dist[j] < nodeValue) {
                    nodeValue = dist[j];
                    nodeIdx = j;
                }
            }
            visit[nodeIdx] = true;

            for (Node n : adjList.get(nodeIdx)) {
                if (dist[n.to] > dist[nodeIdx] + n.w) {
                    dist[n.to] = dist[nodeIdx] + n.w;
                }
            }
        }

        // dist 배열 출력
        StringBuilder sb = new StringBuilder();
        for (int i = 1; i <= V; i++) {
            sb.append(dist[i]).append(" ");
        }
        System.out.println(sb);
    }

}

• Priority Queue 사용

import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;

public class Dijkstra_PriorityQueue {

    static final int INF = 9999999;

    static class Node implements Comparable<Node>{
        int to, w;

        public Node(int to, int w) {
            this.to = to;
            this.w = w;
        }

        @Override
        public int compareTo(Node o) {
            return this.w - o.w;
        }
    }

    public static void main(String[] args) {
        int V = 5;  // 정점의 수
        int E = 6;  // 간선의 수

        // 인접리스트 선언 및 초기화
        ArrayList<ArrayList<Node>> adjList = new ArrayList<>();
        for (int i = 0; i <= V; i++) {
            adjList.add(new ArrayList<>());
        }

        // 인접리스트 입력
        adjList.get(5).add(new Node(1, 1));
        adjList.get(1).add(new Node(5, 1));

        adjList.get(1).add(new Node(2, 2));
        adjList.get(2).add(new Node(1, 2));

        adjList.get(1).add(new Node(3, 3));
        adjList.get(3).add(new Node(1, 3));

        adjList.get(2).add(new Node(3, 4));
        adjList.get(3).add(new Node(2, 4));

        adjList.get(2).add(new Node(4, 5));
        adjList.get(4).add(new Node(2, 5));

        adjList.get(3).add(new Node(4, 6));
        adjList.get(4).add(new Node(3, 6));

        // 시작 정점
        int st = 1;

        int[] dist = new int[V + 1];           // 최소거리 배열
        Arrays.fill(dist, INF);                // 무한대로 초기화
        dist[st] = 0;                          // 시작 정점은 0으로
        boolean[] visit = new boolean[V + 1];  // 방문 체크 배열

        // 우선 순위 큐 사용
        PriorityQueue<Node> pq = new PriorityQueue<>();
        pq.offer(new Node(1, 0));
        while (!pq.isEmpty()) {
            Node cur = pq.poll();

            if (visit[cur.to]) continue;
            visit[cur.to] = true;

            for (Node n : adjList.get(cur.to)) {
                if (!visit[n.to] && dist[n.to] > dist[cur.to] + n.w) {
                    dist[n.to] = dist[cur.to] + n.w;
                    pq.offer(n);
                }
            }
        }

        // dist 배열 출력
        StringBuilder sb = new StringBuilder();
        for (int i = 1; i <= V; i++) {
            sb.append(dist[i]).append(" ");
        }
        System.out.println(sb.toString());
    }

}

시간 복잡도

• 우선순위 큐를 사용하지 않는 다익스트라 알고리즘은 $O(n^2)$의 시간 복잡도를 가진다.
  • 최소의 D[v]를 가진 점 $v_{min}$을 찾는데 $O(n)$ 시간이 걸린다.
  • $v_{min}$에 연결된 점의 수가 최대 (n - 1)개 이므로, 각 D[w]를 갱신하는데 걸리는 시간은 $O(n)$이다.
  • 따라서 시간복잡도는 $(n - 1) * \{O(n) + O(n)\}=O(n^2)$이다.
• 우선순위 큐를 사용하는 다익스트라 알고리즘은 $O(ElogV)$의 시간 복잡도를 가진다.
  • 우선순위 큐에서 꺼낸 정점은 연결된 정점을 탐색하므로 $O(logE)$만큼 반복된다.
  • $E$는 $V^2$보다 항상 작다.
  • $E$개의 간선을 우선순위 큐에서 사용한다.
  • 따라서 시간복잡도는 $O(ElogV)$이다.