[백준]11729: 하노이 탑 이동순서(JAVA)

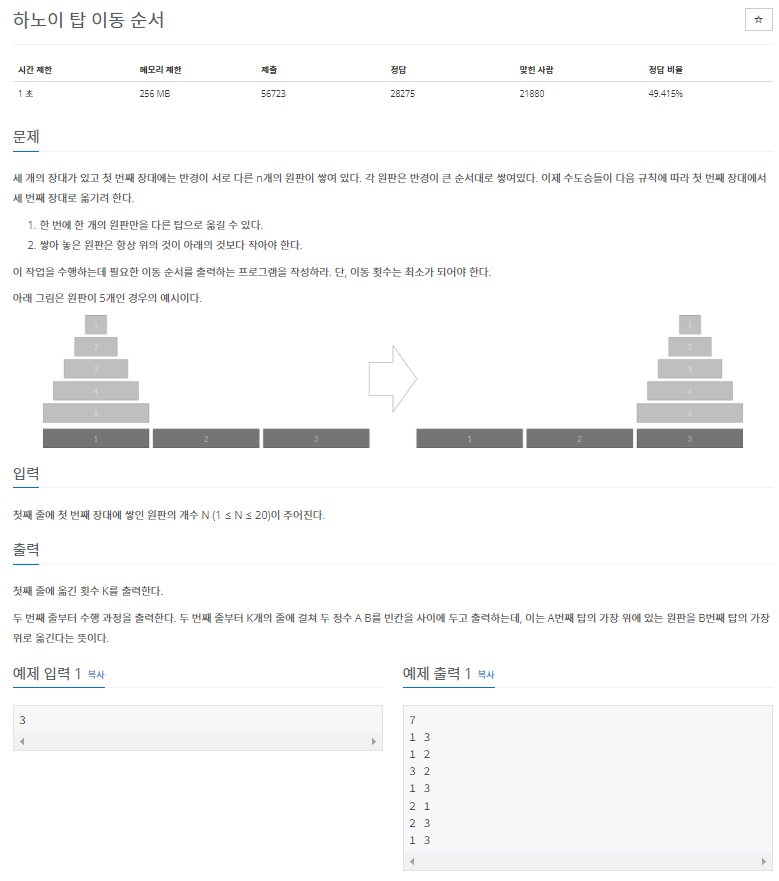
입력값 : 원판의 개수(N)
출력값 : 총 옮긴횟수(K) 및 수행과정

유명한 하노이 탑 알고리즘 문제입니다.
재귀호출 알고리즘에서 대표적인 문제로 공식을 구하는 방법은 검색하면 자세하게 설명되어 있으므로 정보만 공유하고 바로 문제풀이로 들어가겠습니다.

공식 : 일반적으로 원판이 n개 일 때, $2^n -1$번의 이동으로 원판을 모두 옮길 수 있다

[접근방법]

1개, 2개, 3개의 원판을 옮기다 보면 일정한 규칙을 발견할 수 있습니다.

• N개의 원판중 제일 하단의 원판을 옮기기 위해 상단의 원판들을 먼저 이동.
• 이후, 제일 하단의 원판을 목적지로 이동하고 옮겨놓은 나머지 원판들을 다시 목적지로 이동.
• 제일하단의 원판을 옮긴 이후에는 고정이므로 없다고 생각하고 다시 N-1의 원판을 가지고 처음부터 시작

아래의 그림을 보면 조금더 이해하기 쉬울것입니다.
(장대가 숫자일때 헷갈릴 수 있으므로 이미지에 편의상 A,B,C로 대체함)

Ex) 3개의 원판일때 :
   1. 1,2번 원판을 중간 경유지로 이동
   2. 3번원판을 목적지로 이동
   3. 나머지 원판을 다시 목적지로 이동

- N=3일때 시작환경

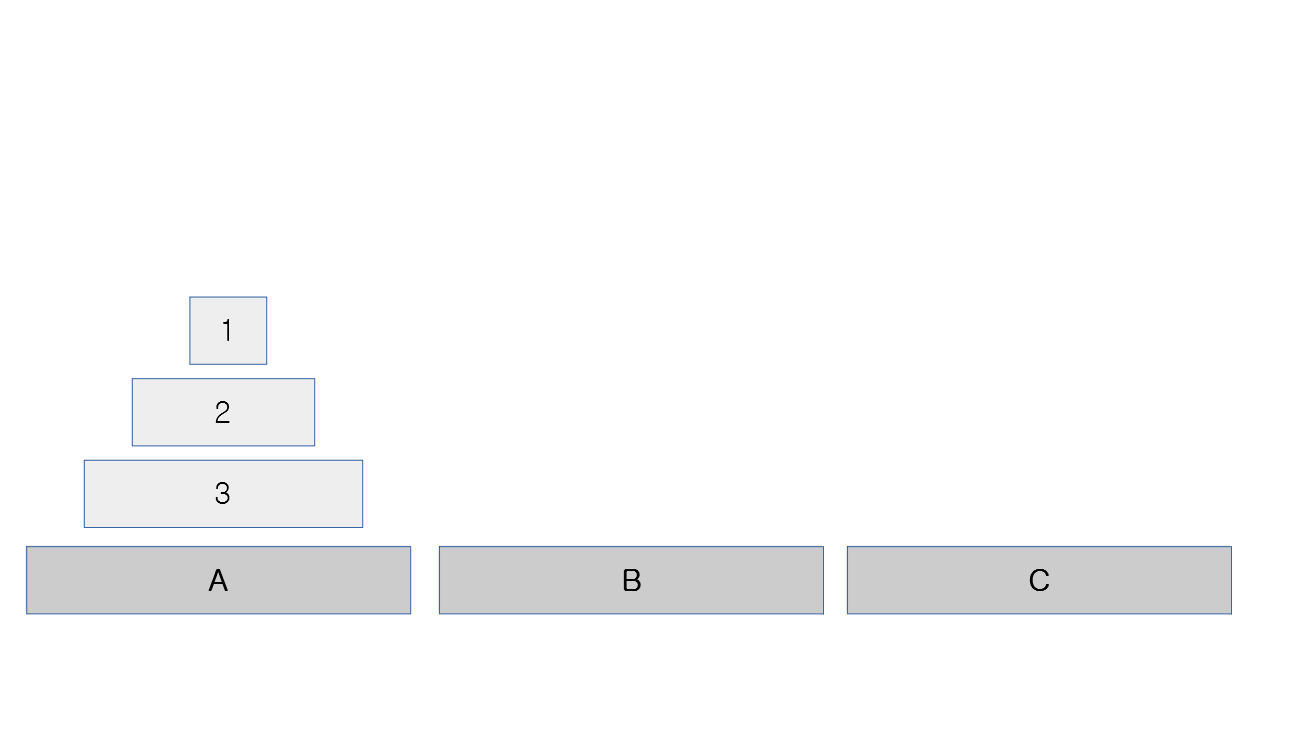
- 맨 하단 원판을 옮기고 난 이후

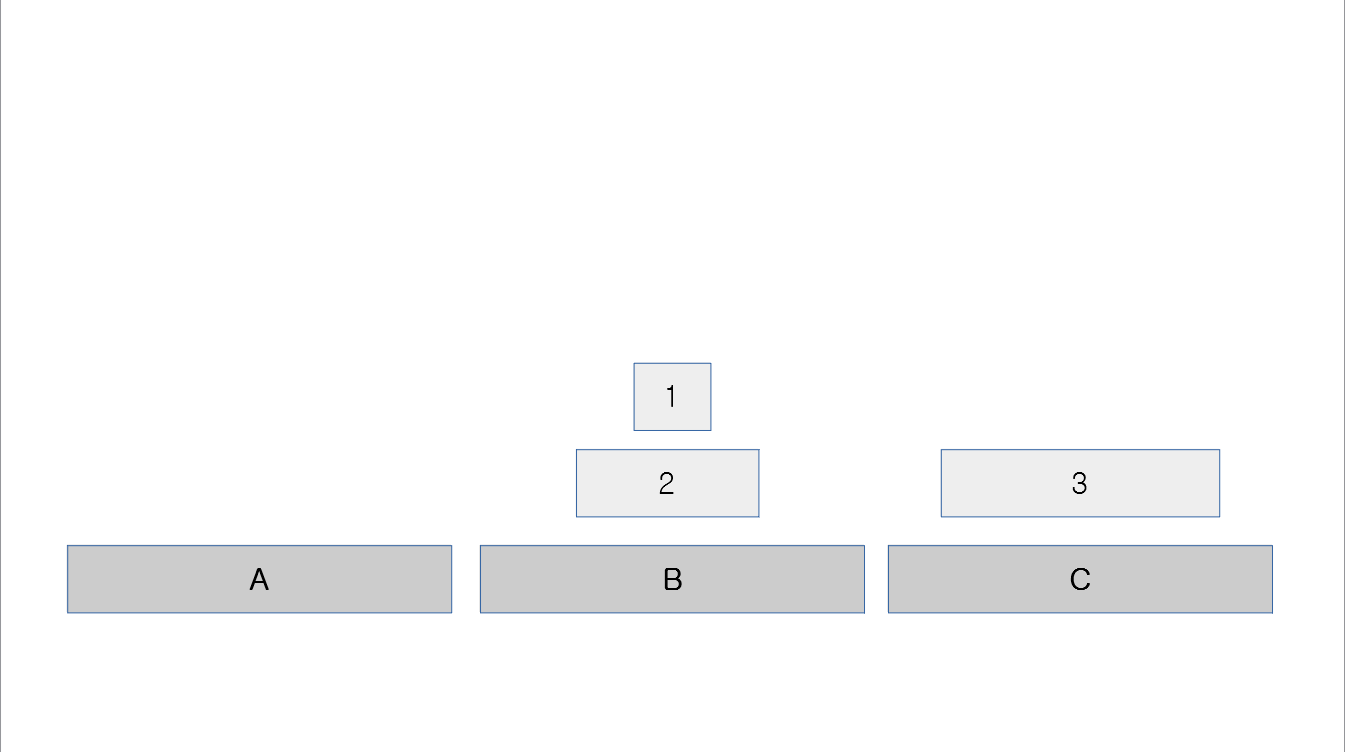
3번 원판은 움직임이 끝남, N-1인 2로 주어졌을때 시작한다고 생각

- N=4일때 맨 하단 원판을 옮기고 난 이후

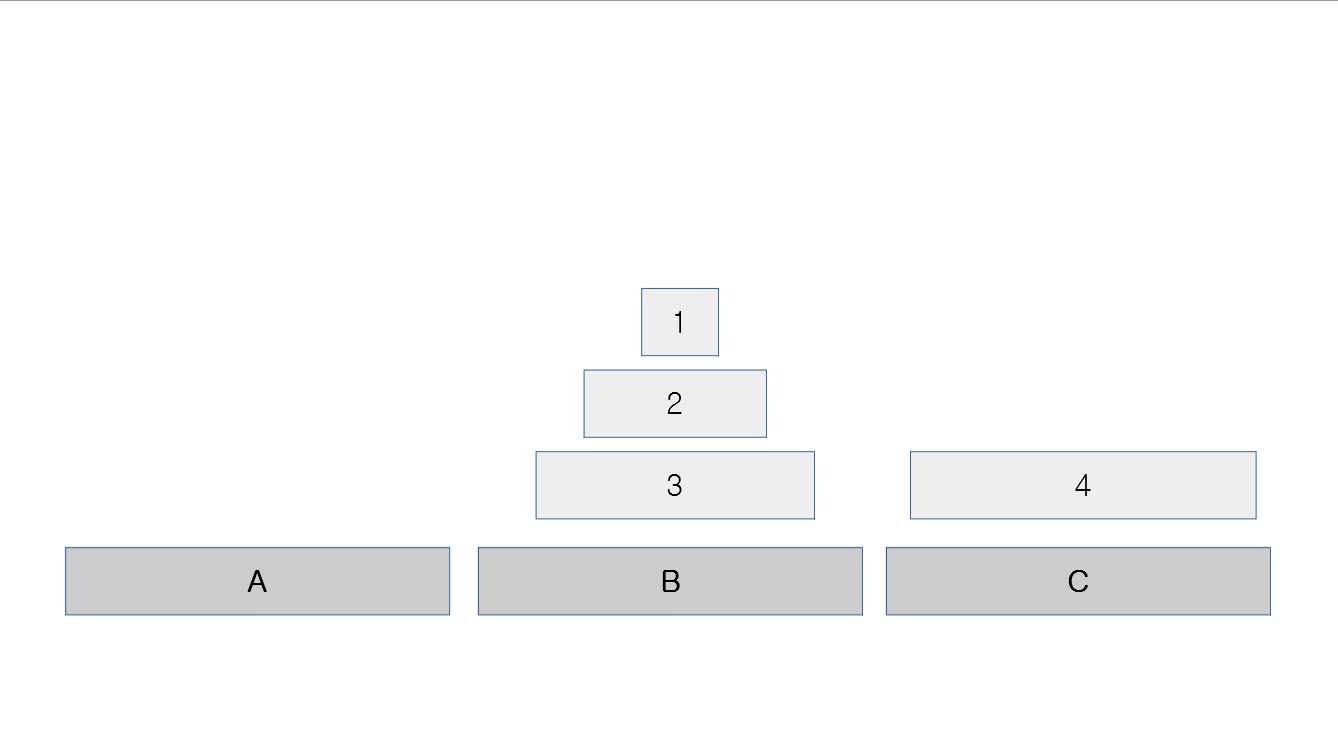
4번 원판을 A에서 C로 옮기고 난 이후의 모습(이후 고정)
N=3일때의 조건으로 다시 시작(시작위치만 A에서 B로 변경)

이제 조금씩 감이 올것입니다. (사실 처음에는 감이 안왔음)

N개의 원판에서 제일 하단의 원판을 옮기는 작업이 끝나면
N-1개의 원판을 옮기는 작업이 실행되는 전형적인 재귀함수의 호출 패턴입니다.
(이때 총 장판의 수는 3개이며 목적지는 C하나로 동일함으로 출발지, 경유지가 바뀐채 실행)

[코드작성]

- 간략한 슈도코드

/*
	N : 원판의 개수 
	start : 출발지 
	mid : 경유지
	to : 목적지
 */
 
fn(N, start, mid, to){
 1. N번째 원판의 상위 원판들을 목적지 옆 경유지로 옮기는 작업
    fn(N-1, start, to, mid)
 2. N번째 원판을 목적지로 이동
 2. 원판의 개수 -1하여 재호출(출발지, 경유지 변경됨)
    fn(N-1, mid, start, to)
}

위 슈도코드가 이해가 된다면 아래와 같이 실제 함수를 작성해 볼 수 있다.
(과정은 StringBuilder로 생성한 'sb' 변수에 저장하여 출력하였다.)

public static void Hanoi(int N, int start, int mid, int to) {
		//횟수 +1
		count++;
				
		// 원판의 수가 1일때 바로 이동
		if (N == 1) {
			sb.append(start + " " + to + "\n");
			return;
		}
 		
        //1. N번째 원판의 상위 원판들을 목적지 옆 경유지로 옮기는 작업
		Hanoi(N - 1, start, to, mid);
    	
        //2. N번째 원판을 목적지로 이동
		sb.append(start + " " + to + "\n");
    	
        //3. 원판의 개수 -1하여 재호출(출발지, 경유지 변경됨)
		Hanoi(N - 1, mid, start, to);
	}

N=3일때 실행과정은 아래와 같으니 이해하는데 도움이 되길 바랍니다.

/*
 N=3일때 함수 실행 과정
 실행횟수 2^n - 1 = 2*2*2 - 1 = 7
 
(실행횟수 출력)7
 
Hanoi(3 1 2 3)
 
Hanoi(2 1 3 2)

Hanoi(1 1 2 3)

(출력)1 3

(출력)1 2

Hanoi(1 3 1 2)

(출력)3 2

(출력)1 3

Hanoi(2 2 1 3)

Hanoi(1 2 3 1)

(출력)2 1

(출력)2 3

Hanoi(1 1 2 3)

(출력)1 3
*/

참조:
https://st-lab.tistory.com/96
https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91