[Data Structure] (2) Graph (Adjacency Matrix, Adjacency List)

Steve·2021년 5월 14일

Graph adjacency list adjacency matrix data structure

웹개발 코스

목록 보기

22/59

Graph
Adjacency matrix
Adjacency list

Graph

컴퓨터 공학에서의 Graph - 여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
정점(vertex)와 정점들을 잇는 간선(edge)가 존재한다.
Tree 도 graph 의 일종이다.
네비게이션, SNS 등

Graph 용어

이름	설명
가중치 그래프 (weighted graph)	edge 에 value 가 있을 때
비가중치 그래프 (unweighted graph)	edge 에 value 가 없을 때
단방향 그래프(directed graph)	한 방향으로만 이어져 있을 때
무방향 그래프 (undirected graph)	양방향으로 이어져 있을 때
진입차수(in-degree)	vertex 에 들어오는 edge 의 수
진출차수(out-degree)	vertex 에서 나가는 edge 의 수
인접(adjacency)	두 vertex를 이어주는 edge이 있다면 두 vertex는 인접한다고 한다.
자기 루프(self loop)	자신에서 나간 edge가 자신으로 돌아올 때
사이클(cycle)	자기 자신으로 돌아올 수 있다면 사이클이 있다고 한다.

Graph 의 표현 방식

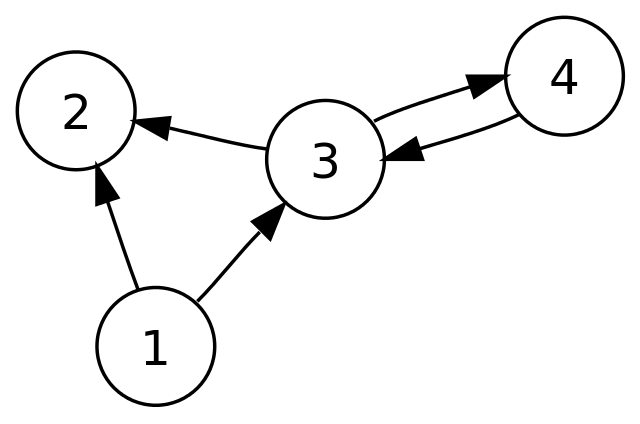
이미지 : http://www2.lawrence.edu/fast/GREGGJ/CMSC250/DataStructures/Graphs.html

1. 인접 행렬 (adjacency matrix)

인접 행렬은 정점간의 인접함을 표시해 주는 행렬로, 2차원 배열의 모습을 가지고 있다. 인접 행렬을 adj[][] 라고 한다면, adj[i][j]에 대해 다음과 같이 정의할 수 있다.

이어져 있으면 1, 아니면 0 이다.
간선에 가중치가 있는 그래프라면 1 대신 가중치를 넣어주는 방식으로 구현할 수 있다.

위 그래프를 배열을 사용하여 인접행렬로 만들면 다음과 같이 된다.

let adjMatrix = 
[
             (to)
          1  2  3  4 
       1 [0, 1, 1, 0]
(from) 2 [0, 0, 0, 0]
       3 [0, 1, 0, 1]
       4 [0, 0, 1, 0]

];
// 1번과 2번의 연결 확인
adjMatrix[0][1] === 1; // true

시간복잡도

정점의 개수를 $V$ 라고 한다면,
1. Vertex to vertex check: $O(1)$
2. Vertex to which vertexes check: $O(V)$
3. Every vertex to which vertexes check: $O(V * V)$

특징

두 정점의 연결 여부를 알고싶은 경우 매우 빠르다.
정점의 개수가 많아지면 많아질수록 한 정점 혹은 모든 정점의 간선 확인은 느려진다.
모든 경우의 수를 0, 1 로 저장하기 때문에 메모리를 많이 차지한다.

2. 인접 리스트 (adjacency list)

인접 리스트는 각 정점이 어떤 정점과 인접한지 리스트의 형태로 볼 수 있는 표현 방식이다. 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트에는 자신과 인접한 다른 정점들이 담겨 있다.

위 그래프를 배열을 사용하여 인접 리스트로 나타내면 아래와 같다.

let adjList = 
[
  1 [2, 3],
  2 [],
  3 [2, 4],
  4 [3]
]

Q) 3번에서 2와 4 중 2가 먼저 나오는 이유
A) 인접 리스트에서 순서는 보통 중요하지 않다. 우선 순위를 구현하고 싶다면 우선 순위별로 정렬하여 담을 수 있다. 하지만 우선 순위를 다루어야 한다면 더 적합한 자료구조(queue, heap)를 사용하는 것이 합리적이기 때문에 보통 중요하지 않다.

시간복잡도

정점의 개수를 $V$ , 간선의 개수를 $E$ 라고 한다면,
1. Vertex to vertex check : $O(E)$
2. Vertex to which vertexes check : $O(E)$
3. Every vertex to which vertexes check: $O(E)$

특징

정점과 정점의 연결 여부 확인에서는 행렬보다 느리다.
한 정점 혹은 모든 정점의 연결 여부를 빠르게 확인할 수 있다.
실제로 연결된 정점 정보만 저장하기 때문에 각 배열의 원소의 합이 간선의 수와 같다. 즉 간선의 수 만큼만 메모리를 차지한다.

코딩테스트에서 그래프, 트리 자료구조 사용하기

Graph도 Stack과 Queue와 마찬가지로 사용자 정의 데이터 타입을 정의하는 게 아닌 배열 혹은 객체로 구현합니다. 문제에서 주어진 간선 혹은 정점들을 2차원 배열이나 객체로 그래프를 구현한 뒤, 해당 그래프를 활용해 탐색 알고리즘과 같이 나머지 로직을 작성하게 됩니다. Tree는 코딩 테스트 내에서 직접 구현하는 게 아닌, 해당 문제가 Graph 혹은 Tree의 구조인지 파악해야 합니다. 그런 다음, Tree의 탐색 방법 및 알고리즘 로직을 통해 문제를 해결합니다.