트리와 그래프의 기본적인 용어에 대해 정리한다.

트리

트리는 하나의 루트 노드를 갖는다.
루트 노드는 0개 이상의 자식 노드를 갖고 있다.
그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고,이는 재귀적으로 반복 정의가 된다.

class Node{
	public String name;
    public Node[] children

}

이진트리

각 노드가 최대 두개의 자식을 갖는 트리를 뜻한다.
모든 트리가 이진 트리는 아니다.

이진 탐색 트리

아래와 같은 속성을 가진 트리를 뜻한다.
'왼쪽 자식 노드<=n(부모 노드)< 오른쪽 자식 노드'속성은 모든 노드 n에 대해서 반드시 참이다.

완전 이진 트리(Complete Binary Tree)

K층의 트리가 존재할때 K-1까진 퍼펙트 이진 트리이고 K층에선 완벽하진 않아도 왼쪽부터 채워져 있는 구조의 트리를 완전 이진 트리라 한다.

전 이전 트리(Full Binary Tree)

모든 자식 노드의 자식이 없거나 정확히 두개가 있는 경우를 뜻한다.

포화 이진 트리(perfect Binary Tree)

전 이진트리이면서 완전 이진트리인 경우를 말한다.
마지막 단계가 전부 채워져있어야 한다.

이진 트리 순회

전위, 중위 ,후위 순회가 사용된다.
그중 중위 순회가 가장 빈번하게 사용된다.

중위 순회
왼쪽 가지 ->현재 노드->오른쪽 가지 순서로 노드를 방문하고 출력한다.

void inOrderTravelesal(TreeNode node){
	if(node!=null){
    inOrderTravelesal(node.left);
    visit(node);
    inOrderTravelesal(node.right);
   }
 }

전위 순회
자식 노드보다 현재 노드를 먼저 방문하는 방법을 말한다.

void preOrderTravelesal(TreeNode node){
	if(node!=null){
    visit(node);
    preOrderTravelesal(node.left);
    preOrderTravelesal(node.right);
   }
 }

후위 순회
모든 자식 노드를 먼저 방문한 뒤 마지막에 현재 노드를 방문하는 방법을 말한다.

void postOrderTravelesal(TreeNode node){
	if(node!=null){
    postOrderTravelesal(node.left);
    postOrderTravelesal(node.right);
    visit(node);

   }
 }

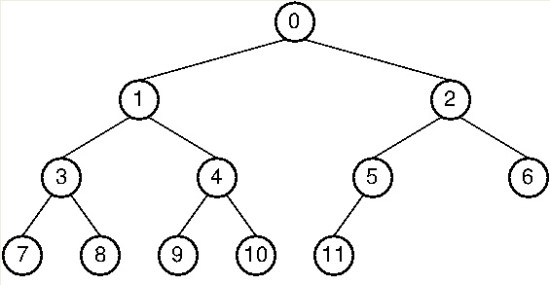
중위 순회 : 7->3->8->1->9->4->10->0->11->5->2->6

전위 순회 : 0->1->3->7->8->4->9->10->2->5->11->6

후위 순회 : 7->8->3->9->10->4->1->11->5->6->2->0

힙

힙은 MAX-Heap과 MIn-Heap으로 나뉘는데 최소힙은
오름차순으로 최대힙은 내림차순으로 정렬된다는것 외에는 같은 구조이다.

그래프