문제

Programmers Lv3, 가장 긴 팰린드롬

핵심

• 입력의 크기가 2,500이라 대략 $O(N^2)$이하 알고리즘을 사용한다. 앞뒤를 뒤집어도 똑같은 문자열을 팰린드롬(palindrome)이라고 한다. 문자열 s가 주어질 때, s의 부분 문자열 중 가장 긴 팰림드롬의 길이를 반환한다.
• 팰린드롬 여부를 확인하는 함수는 아래와 같이 구할 수 있다.

boolean isPalinDrome(String s, int l, int r) {
	while (l <= r) {
		if (s.charAt(l) == s.charAt(r)) {
			++l;
			--r;
		} else {
			return false;
		}
	}
	return true;
}

1. 모든 부분 문자열 구한 후 팰린드롬 구하기

• 가능한 부분 문자열의 시작 인덱스, 끝 인덱스를 구한 후 팰린드롬 여부를 검사한다. 가능한 좌표는 아래와 같이 이중 반복문으로 모두 구할 수 있다. 팰린드롬을 만들 수 있다면, 가장 긴 길이가 되도록 갱신한다.

for (int i = 0; i < n; i++) {
	for (int j = i; j < n; j++) {
		if (isPalinDrome(s, i, j)) {
			int len = j - i + 1;
				if (ans < len) {
					ans = len;
				}
			}
		}
	}
}

시간복잡도

• 시간복잡도는 $O(n^3)$에 동작하지만, n이 크지 않고 팰린드롬 함수에서 매번 최대 길이를 검사하지 않고, 인덱스가 두 개씩 이동해서 그런지 생각보다 빠르게 동작한다. n이 더 컸다면 시간 초과가 났을 것이다.
  

전체 코드

class Solution {
	public int solution(String s) {
		int n = s.length();
		
		int ans = 1;
		for (int i = 0; i < n; i++) {
			for (int j = i; j < n; j++) {
				if (isPalinDrome(s, i, j)) {
					int len = j - i + 1;
					if (ans < len) {
						ans = len;
					}
				}
			}
		}
		return ans;
	}
	
	boolean isPalinDrome(String s, int l, int r) {
		while (l <= r) {
			if (s.charAt(l) == s.charAt(r)) {
				++l;
				--r;
			} else {
				return false;
			}
		}
		return true;
	}
}

2. 중심으로부터 팰린드롬 길이 확장하기

• 중심 인덱스부터 팰린드롬의 길이를 구하는 방식으로 최적화할 수 있다. 하나의 중심으로부터 시작할 수 있고(홀수 팰린드롬), 나란히 붙어 있는 두 개의 중심(짝수 팰린드롬)으로 시작할 수 있다.
• 문자열의 길이가 7이라면, 아래와 같은 인덱스에서 퍼져나간다고 생각하면 된다.

// helloeh 7
홀수: {0, 0} -> h                   
짝수: {0, 1} -> h e
홀수: {1, 1} -> e
짝수: {1, 2} -> e l
...
홀수: {6} -> h
짝수: {6, 7} -> h, outofbound

• 홀수 시작 좌표와 짝수 시작 좌표에 대한 팰린드롬 길이를 구한다. 기존 팰린드롬 로직에서 길이 로직만 추가되었다. 홀수 팰린드롬을 구할 때 시작 좌표가 같아도 길이를 +2하므로 결과값에서 -1을 한다.

for (int i = 0; i < n; i++) {
	ans = Math.max(ans, getPalindromeLength(s, i, i) - 1);
	ans = Math.max(ans, getPalindromeLength(s, i, i + 1));
}

int getPalindromeLength(String s, int l, int r) {
	int n = s.length();

	int len = 0;
	while (l >= 0 && r < n) {
		if (s.charAt(l) == s.charAt(r)) {
			len += 2;
			--l;
			++r;
		} else {
			break;
		}
	}
	return len;
}

시간복잡도

• $O(n^2)$
  

전체 코드

class Solution {
	public int solution(String s) {
		int n = s.length();

		int ans = 0;
		for (int i = 0; i < n; i++) {
			ans = Math.max(ans, getPalindromeLength(s, i, i) - 1);
			ans = Math.max(ans, getPalindromeLength(s, i, i + 1));
		}

		return ans;
	}

	int getPalindromeLength(String s, int l, int r) {
		int n = s.length();

		int len = 0;
		while (l >= 0 && r < n) {
				if (s.charAt(l) == s.charAt(r)) {
						len += 2;
						--l;
						++r;
				} else {
						break;
				}
		}

		return len;
	}
}

3. DP

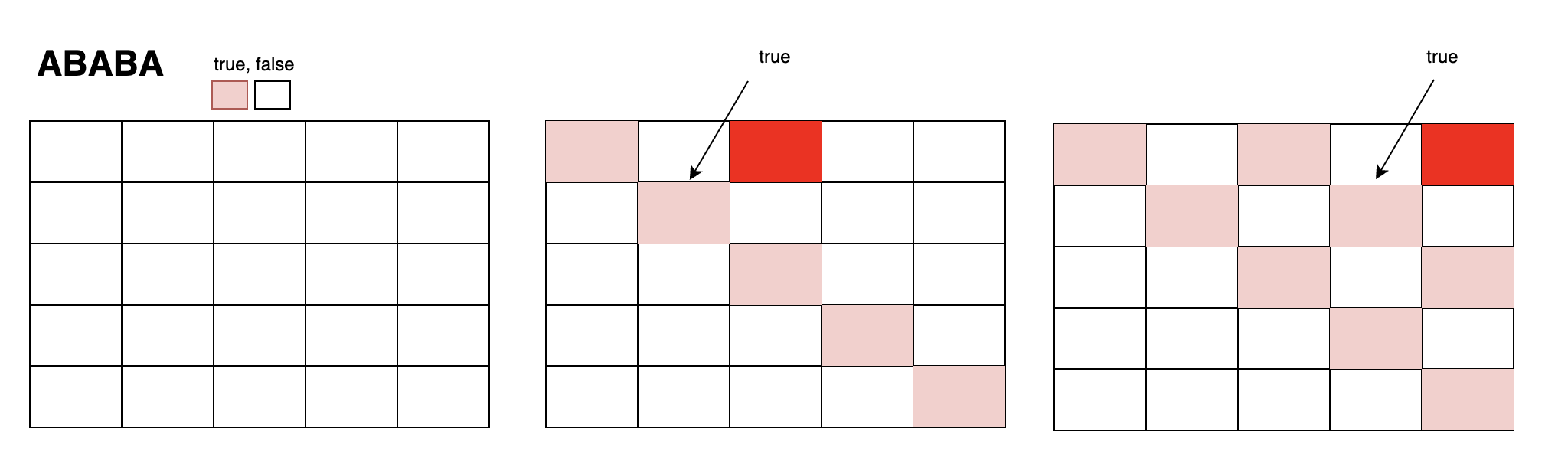
• 모든 길이가 1인 부분 문자열은 팰린드롬이고, 길이가 2일 때 두 문자가 동일한 경우에도 팰린드롬이다.
• 길이가 3 이상인 경우 양 끝 문자가 같고, 사이에 있는 부분 문자열이 팰린드롬일 때 해당 부분 문자열은 팰린드롬이다.

dp[i][i] = true // 길이가 1인 부분 문자열은 팰린드롬

if (s[i] == s[i + 1]) {
  dp[i][i + 1] = true // 두 문자가 같다면 i와 i+1 부분 문자열은 팰린드롬  
  ans = 2;
}

• 예를 들어 길이가 3일 때 i가 0이고, j가 2인 경우 s[i]와 s[j]가 같고, i와 j 사이에 있는 부분 문자열이 팰린드롬이어야 한다. 따라서 dp[i + 1][j - 1]이 true일 때 dp[i][j]가 true가 될 수 있다.
  

시간복잡도

• $O(n^2)$
  

전체 코드

class Solution {
    public int solution(String s) {
        int n = s.length();
        
        boolean[][] dp = new boolean[n][n];
        int ans = 1;

        for (int i = 0; i < n; ++i) {
            dp[i][i] = true;
            if (i < n - 1 && s.charAt(i) == s.charAt(i + 1)) {
                dp[i][i + 1] = true;
                ans = 2;
            }
        }

        for (int len = 3; len <= n; ++len) {
            for (int i = 0; i < n - len + 1; ++i) {
                int j = i + len - 1;
                
                if (dp[i + 1][j - 1] && s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = true;
                    ans = len;
                }
            }
        }

        return ans;
    }
}