문제

Programmers Lv3, 단속카메라

핵심

• 입력의 크기가 25라 대략 $O(N^*2)$이하 알고리즘을 사용한다.
• 경주로 건설 비용을 구해야 한다. 직선 도로는 100원, 방향이 달라지면 600원이 든다. 이때 {0, 0}에서 출발하여 {r - 1, c - 1}까지 도로를 건설하는 최소 비용을 구해야 한다.
• 본 문제는 완전 탐색 문제이다. 일반적인 bfs와 달리 최소 비용을 구하기 위해 방문했던 경로를 또 방문할 수 있어야 한다.
• 사용한 자료 구조
  • bfs 탐색을 위해 y, x 좌표를 사용한다.
  • 현재 방문한 곳의 비용을 저장하기 위해 cost를 사용한다. 방문했던 경로를 또 방문할 때 어떻게 종료 조건을 설정할 수 있을까? 경로 비용을 매우 높은 값으로 초기화하고, 방문했던 경로보다 더 비용이 크다면 그 경로를 방문하지 않으면 된다! 기존 경로 비용에다 방향이 같다면 100원을 추가하고, 다르다면 600원을 추가하는 식으로 동작한다. 방향 검사를 위해 dir를 사용한다.

Queue<int[]> q = new LinkedList<>(); // y, x, cost, dir
q.add(new int[]{0, 0, 0, -1});

int[][][] costs = new int[r][c][4];

왜 cost를 3차원 배열로 사용할까?

• 처음엔 2차원 배열로 사용하였다. 하지만, 이 경우 현재까지 비용이 더 크더라도 이후 커브 횟수가 적어 총 비용이 낮아지는 반례를 놓치게 된다. 비용 경로에 방향까지 추가하면 이러한 반례까지 잡아낼 수 있다. 해당 반례를 그림으로 나타내면 아래와 같다.
  
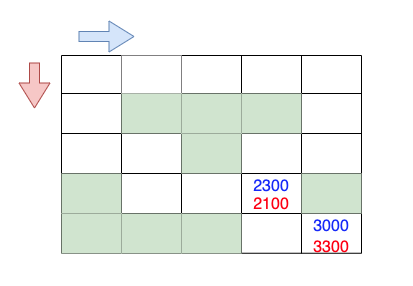
• 방향을 고려하지 않으면, 파란색으로 시작한 경우 금액이 더 크므로 탐색을 추가로 하지 못한다.

개선

코드

import java.util.*;

class Solution {
    int dy[] = {1, 0, -1, 0};
    int dx[] = {0, 1, 0, -1};
    int ans = Integer.MAX_VALUE;
    
    void bfs(int[][] board) {
        int r = board.length;
        int c = board[0].length;
        int[][][] costs = new int[r][c][4];
        for (int i = 0; i < r; ++i) {
            for (int j = 0; j < c; ++j) {
                Arrays.fill(costs[i][j], Integer.MAX_VALUE);
            }
        }
        
        Queue<int[]> q = new LinkedList<>(); // y, x, cost, dir
        q.add(new int[]{0, 0, 0, -1});
        while (!q.isEmpty()) {
            var cur = q.poll();
            int y = cur[0];
            int x = cur[1];
            int cost = cur[2];
            int d = cur[3];
            
            if (y == r - 1 && x == c - 1) {
                ans = Math.min(ans, costs[y][x][d]);
                continue;
            }
            for (int dir = 0; dir < 4; ++dir) {
                int ny = y + dy[dir];
                int nx = x + dx[dir];
                int ncost = 0;
                if (ny < 0 || ny >= r || nx < 0 || nx >= c) continue;
                if (board[ny][nx] == 1) continue;
                
                if (d == dir || d == -1) ncost += cost + 100;
                else ncost += cost + 600;
                
                if (ncost <= costs[ny][nx][dir]) {
                    costs[ny][nx][dir] = ncost;
                    q.add(new int[]{ny, nx, ncost, dir});
                }
            }
        }
    }
    public int solution(int[][] board) {
        
        bfs(board);
        
        return ans;
    }
}