문제

Programmers Lv3, 양과 늑대

핵심

• 특정 노드에 방문할 때마다 해당 노드에 있던 양과 늑대가 따라온다. 루트 노드에서 출발하여 양과 늑대를 모을 때, 최대한 많이 모을 수 있는 양의 개수를 반환한다. 늑대의 수가 양보다 많거나 같아지면 양이 잡아먹히니, 잡아먹히지 않도록 경로를 선정해야 한다.
  
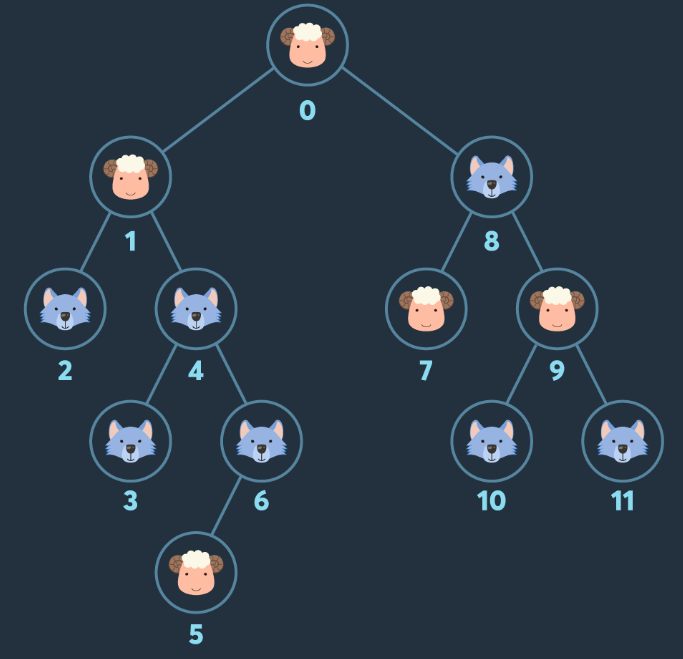
• 위의 예시에선 루트노드(양1)에서 8번 노드로 가게되면 늑대와 양의 수가 같아 잡아먹힌다. 따라서 1번 노드(양2)를 방문하고 8번 노드(양2, 늑1)를 방문하면 양이 잡아먹히지 않는다. 이후 7번(양3, 늑1), 9번(양4, 늑1), 4번(양4, 늑2), 6번(양4, 늑3), 5번 노드(양5, 늑3)를 방문해서 최대 모을 수 있는 양의 수는 5마리인 것을 알 수 있다.
• 현재 방문한 정점을 기준으로 모든 경로를 탐색할 수 있어야 한다. 따라서 완전 탐색을 하기 위해 DFS 알고리즘을 사용한다.
• 문제를 풀기 위해 크게 두 가지 작업을 한다.
  1. 입력 자료 구조 파씽(트리)
  2. 양을 모을 수 있는 가능한 경로를 탐색하면서 최대 양 개수 반환

1. 입력 자료 구조를 트리로

[[0,1],[1,2],[1,4],[0,8],[8,7],[9,10],[9,11],[4,3],[6,5],[4,6],[8,9]]

• 간선의 정보가 위처럼 주어질 때, 첫 번째 원소는 부모를 가리키고 두 번째 원소는 자식을 가리킨다. 그림을 보면 1번의 왼쪽 자식에 2번과 4번이 있다. 이를 처리하기 위해 왼쪽 자식부터 처리한다.

Arrays.fill(lc, -1);
Arrays.fill(rc, -1);
for (int i = 0; i < n - 1; ++i) {
	if (lc[edges[i][0]] == -1) 
		lc[edges[i][0]] = edges[i][1];
	else 
		rc[edges[i][0]] = edges[i][1];
}

2. 완전 탐색(dfs)

• 루트노드부터 출발하여 해당 노드에서 탐색 가능한 왼쪽, 오른쪽 자식이 있다면 탐색할 수 있는 다음 경로에 추가한다. 문제 예시에서 1번과 8번 노드를 차례로 넣은 후 탐색을 시작한다. 여기에서 주의할 것이 있다. 되돌아오는 것을 고려하기 위해 이미 탐색했던 노드를 제거하면 안 된다. 이를 위해 DFS를 탐색하기 전에 왼쪽과 오른쪽 자식을 추가한 다음 경로를 복사해 주었다.

if (lc[cur] != -1) nxts.add(lc[cur]);
if (rc[cur] != -1) nxts.add(rc[cur]);

for (var nxt : nxts) {
	List<Integer> tmps = new ArrayList<>(nxts);
	tmps.remove((Integer)nxt);
	dfs(nxt, sheep, wolf, tmps, lc, rc, info);
} 

• 현재 노드를 방문했을 때 양과 늑대를 센다. 늑대가 양보다 같거나 많다면 더 탐색할 필요 없으므로 종료하고, 양이 더 많다면 양의 개수를 정답에 갱신한다.

if (info[cur] == 0) 
	++sheep;
else 
	++wolf;

if (sheep <= wolf) 
	return;

ans = Math.max(ans, sheep);

개선

• 되돌아오는 것을 고려하는 과정에서 이미 방문했던 곳도 재방문하게 된다. 메모이제이션을 사용하지 않은 피보나치 수열처럼 하나의 함수에서 두개의 함수(왼쪽, 오른쪽)을 호출하게 된다. 메모이제이션을 이용해 성능을 개선해볼 수 있을 거 같은데, 이를 고려하지 않아도 빠른 시간에 통과가 되므로 넘어간다.

시간복잡도

• $O(2^n)$, n은 최대 17
  

코드

import java.util.*;

class Solution {
    
    int ans = 0;
    public int solution(int[] info, int[][] edges) {
        
        int n = info.length;
        int[] lc = new int[n];
        int[] rc = new int[n];
        int[] sheep = new int[n];
        
        Arrays.fill(lc, -1);
        Arrays.fill(rc, -1);
        for (int i = 0; i < n - 1; ++i) {
            if (lc[edges[i][0]] == -1) 
                lc[edges[i][0]] = edges[i][1];
            else 
                rc[edges[i][0]] = edges[i][1];
        }
        
        dfs(0, 0, 0, new ArrayList<>(), lc, rc, info);
        
        return ans;
    }
    
    void dfs(int cur, int sheep, int wolf, List<Integer> nxts, int[] lc, int[] rc, int[] info) {
        
        if (info[cur] == 0) 
            ++sheep;
        else 
            ++wolf;
        
        if (sheep <= wolf) 
            return;
        
        ans = Math.max(ans, sheep);
        
        if (lc[cur] != -1) nxts.add(lc[cur]);
        if (rc[cur] != -1) nxts.add(rc[cur]);
        
        for (var nxt : nxts) {
            List<Integer> tmps = new ArrayList<>(nxts);
            tmps.remove((Integer)nxt);
            dfs(nxt, sheep, wolf, tmps, lc, rc, info);
        }  
    }
}