문제

Programmers, 전력망을 둘로 나누기

핵심

• 입력의 크기가 $10^2$이라 구현에 초점을 맞춘다.
  
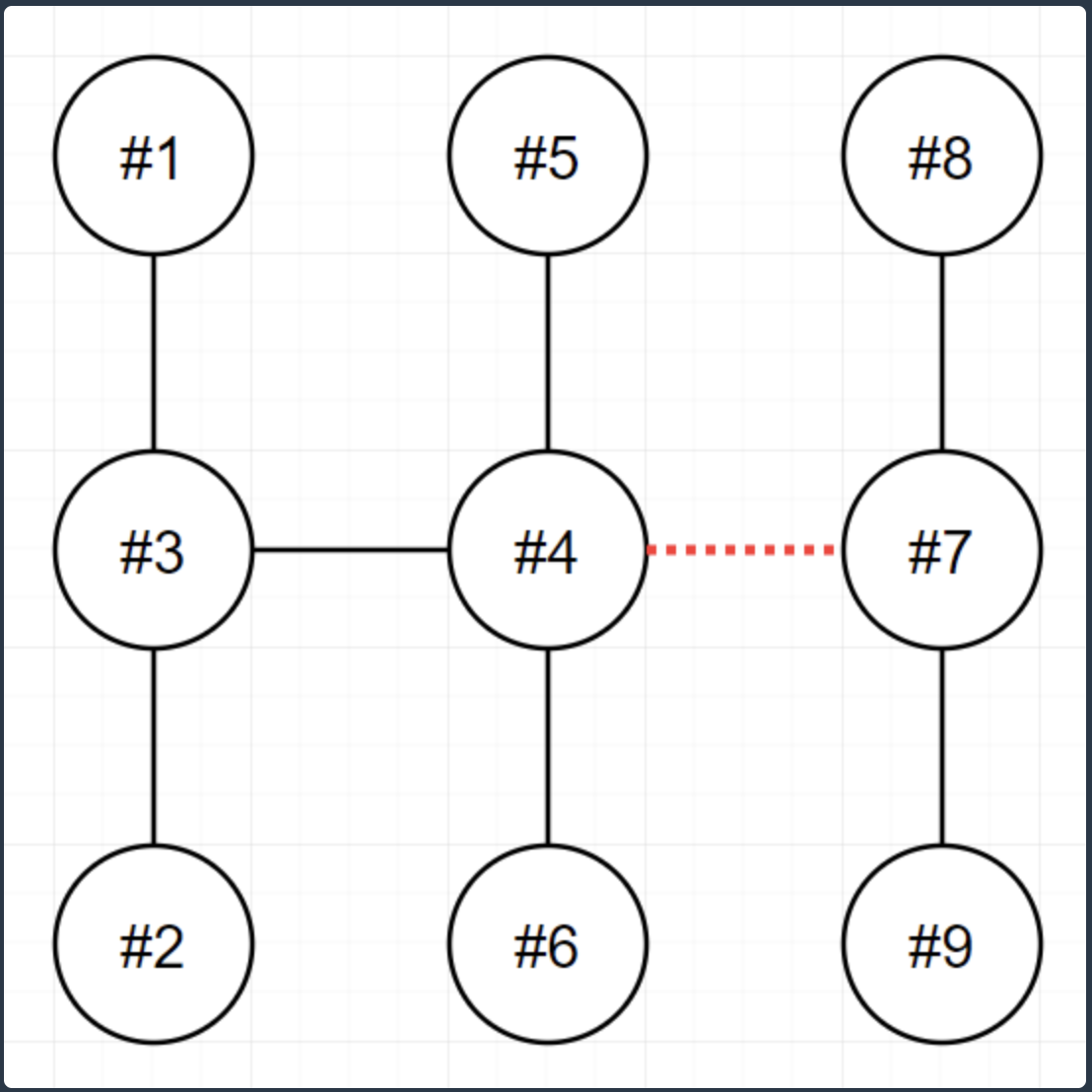
• n 개의 송전탑이 트리 형태로 연결되어 있을 때 전선 중 하나를 끊어 2개로 분할하려고 한다. 이때 분할된 전력망이 갖는 개수를 최대한 비슷하게 맞출 때 그 차이를 구하는 문제이다. 완전 탐색 문제로 전선을 하나씩 끊어보면서 분리된 전력망의 개수 차이가 가장 적은 경우를 구하면 된다.
• 먼저 연결된 전선을 끊는다는 것은 a -> b로 전선이 연결되어 있을 때 해당 전선을 방문 표시하고 a에서 출발하거나 a에 도착하는 모든 간선을 방문하면 된다. 이를 코드로 나타내면 다음과 같다.

queue<int> q;
isvisited[i] = true; // i번째 전선 끊기
q.push(wires[i][0]); // a에서 출발
int cnt = 0;
while (!q.empty()) {
	auto cur = q.front(); q.pop();
	++cnt;
	for (int j = 0; j < wires.size(); ++j) { // 모든 전선 탐색
		if (i == j || isvisited[j]) // 끊은 전선, 방문한 전선 건너뛰기
			continue;
		if (wires[j][0] == cur) { // a에서 출발하는 전선
			isvisited[j] = true;
			q.push(wires[j][1]);
		}
		if (wires[j][1] == cur) { // a로 도착하는 간선
			isvisited[j] = true;
			q.push(wires[j][0]);
		}
	}
}

개선

#include <string>
#include <vector>
#include <queue>
#include <iostream>
#include <algorithm>

using namespace std;
int ans = 1e9;
int solution(int n, vector<vector<int>> wires) {
    int answer = -1;
    for (int i = 0; i < wires.size(); ++i) {
        bool isVisited[101] = {};
        queue<int> q;
        isVisited[i] = true;
        q.push(wires[i][0]);
        int cnt = 0;
        while (!q.empty()) {
            auto cur = q.front(); q.pop();
            ++cnt;
            for (int j = 0; j < wires.size(); ++j) {
                if (i == j || isVisited[j])
                    continue;
                if (wires[j][0] == cur) {
                    isVisited[j] = true;
                    q.push(wires[j][1]);
                }
                if (wires[j][1] == cur) {
                    isVisited[j] = true;
                    q.push(wires[j][0]);
                }
            }
        }
        int diff = abs(n - cnt - cnt);
        ans = min(ans, diff);
    }
    return ans;
}

• 해당 코드는 개선할 부분이 있다. 연결된 전선을 찾기 위해 매번 모든 전선을 탐색해야 한다. 그래프 자료구조를 이용하면 모든 전선을 탐색하는 대신 연결된 전선만 탐색이 가능하다. 그렇기 위해선 먼저 인접 행렬 또는 인접 리스트를 통해 각 정점의 연결 상태를 그래프로 표현한다.

코드

시간복잡도

• e 간선, v 정점일 때 $O(e \times (v + e))$

C++

#include <vector>
#include <queue>
#include <iostream>
#include <algorithm>

using namespace std;
int ans = 1e9;
void bfs(int st, vector<vector<int>>& graph, vector<bool>& isVisited, int n) {
    queue<int> q;
    q.push(st);
    isVisited[st] = true;
    int cnt = 0;
    while (!q.empty()) {
        auto cur = q.front(); q.pop();
        cnt++;
        for (int next : graph[cur]) { 
            if (!isVisited[next]) {
                isVisited[next] = true;
                q.push(next);
            }
        }
    }
    int diff = abs(n - cnt - cnt);
    ans = min(ans, diff);
}

int solution(int n, vector<vector<int>> wires) {
    vector<vector<int>> graph(n + 1);
    for (auto& wire : wires) {
        graph[wire[0]].push_back(wire[1]);
        graph[wire[1]].push_back(wire[0]);
    }
    for (auto& wire : wires) {
        vector<bool> isVisited(n + 1, false);
        isVisited[wire[0]] = true;
        bfs(wire[1], graph, isVisited, n);
    }
    return ans;
}

Java

import java.util.*;

class Solution {
    private int ans = Integer.MAX_VALUE;
    
    private void bfs(int start, ArrayList<ArrayList<Integer>> graph, boolean[] isVisited, int n) {
        Queue<Integer> q = new LinkedList<>();
        q.offer(start);
        isVisited[start] = true;
        int cnt = 0;
        while (!q.isEmpty()) {
            int current = q.poll();
            cnt++;
            for (int next : graph.get(current)) {
                if (!isVisited[next]) {
                    isVisited[next] = true;
                    q.offer(next);
                }
            }
        }
        int diff = Math.abs(n - cnt - cnt);
        ans = Math.min(ans, diff);
    }
    
    public int solution(int n, int[][] wires) {
        ArrayList<ArrayList<Integer>> graph = new ArrayList<>(n + 1);
        for (int i = 0; i <= n; ++i)
            graph.add(new ArrayList());
        for (var wire : wires) {
            graph.get(wire[0]).add(wire[1]);
            graph.get(wire[1]).add(wire[0]);
        }
        for (var wire : wires) {
            boolean[] isVisited = new boolean[n + 1];
            isVisited[wire[0]] = true;
            bfs(wire[1], graph, isVisited, n);
        }
        return ans;
    }
}