01-4. 그리디 알고리즘 문제풀이

📝문제1. 백준 11399번

- 문제

https://www.acmicpc.net/problem/11399
인하은행에는 ATM이 1대밖에 없다. 지금 이 ATM앞에 N명의 사람들이 줄을 서있다. 사람은 1번부터 N번까지 번호가 매겨져 있으며, i번 사람이 돈을 인출하는데 걸리는 시간은 Pi분이다.

사람들이 줄을 서는 순서에 따라서, 돈을 인출하는데 필요한 시간의 합이 달라지게 된다. 예를 들어, 총 5명이 있고, P1 = 3, P2 = 1, P3 = 4, P4 = 3, P5 = 2 인 경우를 생각해보자. [1, 2, 3, 4, 5] 순서로 줄을 선다면, 1번 사람은 3분만에 돈을 뽑을 수 있다. 2번 사람은 1번 사람이 돈을 뽑을 때 까지 기다려야 하기 때문에, 3+1 = 4분이 걸리게 된다. 3번 사람은 1번, 2번 사람이 돈을 뽑을 때까지 기다려야 하기 때문에, 총 3+1+4 = 8분이 필요하게 된다. 4번 사람은 3+1+4+3 = 11분, 5번 사람은 3+1+4+3+2 = 13분이 걸리게 된다. 이 경우에 각 사람이 돈을 인출하는데 필요한 시간의 합은 3+4+8+11+13 = 39분이 된다.

줄을 [2, 5, 1, 4, 3] 순서로 줄을 서면, 2번 사람은 1분만에, 5번 사람은 1+2 = 3분, 1번 사람은 1+2+3 = 6분, 4번 사람은 1+2+3+3 = 9분, 3번 사람은 1+2+3+3+4 = 13분이 걸리게 된다. 각 사람이 돈을 인출하는데 필요한 시간의 합은 1+3+6+9+13 = 32분이다. 이 방법보다 더 필요한 시간의 합을 최소로 만들 수는 없다.

줄을 서 있는 사람의 수 N과 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어졌을 때, 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 구하는 프로그램을 작성하시오.

입력
첫째 줄에 사람의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어진다. (1 ≤ Pi ≤ 1,000)

출력
첫째 줄에 각 사람이 돈을 인출하는데 필요한 시간의 합의 최솟값을 출력한다.

예제 입력 1 : 5 / 3 1 4 3 2
예제 출력 1 : 32

- 나의 코드💻

n = int(input())
plist = list(map(int, input().split()))
plist.sort()

k = 0
alist = []

for i in range(n):
    k = k + plist[i]
    alist.append(k)

min = sum(alist)
print(min)

- 과정📖

문제에서 설명을 1번 사람, 2번 사람으로 했기에 조금 헷갈렸다. 그래서 사람을 a, b, c, d, e로 구분했다. a - 3, b - 1, c - 4, d - 3, e - 2 라고 하면 이해가 조금 쉬워진다. 설명에서도 쓰여 있듯, 시간이 가장 적은 사람 순인 b - e - a - d - c 순서로 줄을 섰을 때 가장 시간이 적게 걸렸다. 즉, 돈을 인출하는데 걸리는 시간이 적은 사람 순으로 오름차순 정렬을 할 때에 시간의 합이 최소가 된다.

• 헷갈렸던 문법
  sum(alist) -> alist라는 리스트 내의 모든 원소를 합쳐준다.

---

📝문제2. 백준 11047번

- 문제

https://www.acmicpc.net/problem/11047

준규가 가지고 있는 동전은 총 N종류이고, 각각의 동전을 매우 많이 가지고 있다. 동전을 적절히 사용해서 그 가치의 합을 K로 만들려고 한다. 이때 필요한 동전 개수의 최솟값을 구하는 프로그램을 작성하시오.

입력
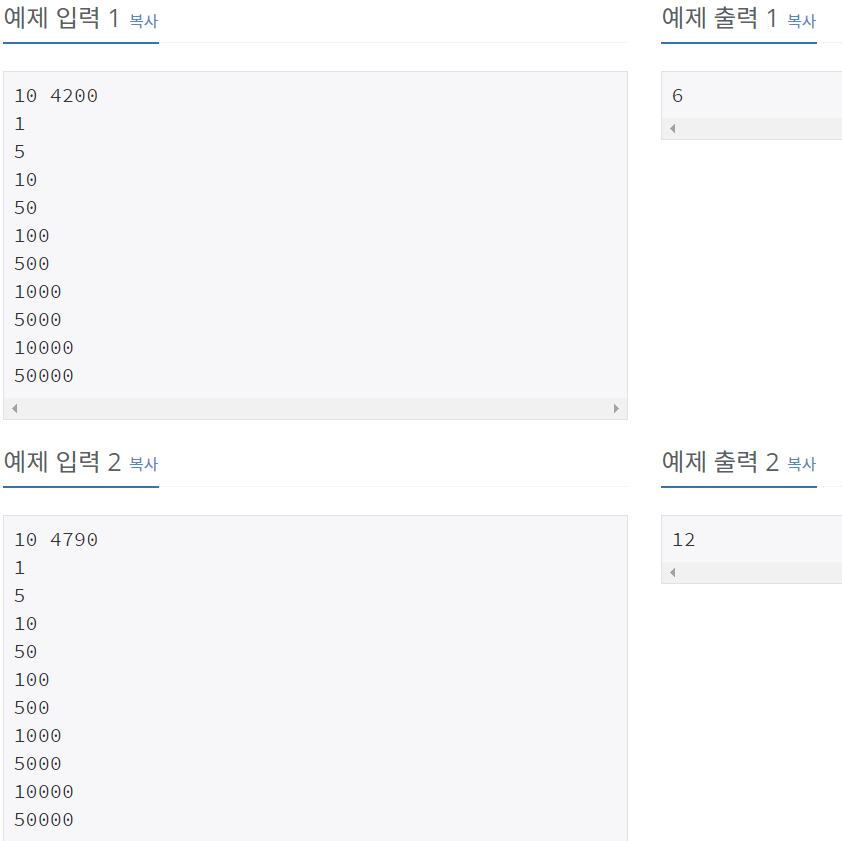
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 10, 1 ≤ K ≤ 100,000,000)
둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)

출력
첫째 줄에 K원을 만드는데 필요한 동전 개수의 최솟값을 출력한다.

- 나의 코드💻

from itertools import combinations

n, k = map(int, input().split())
alist = []
for i in range(n):
    alist.append(int(input()))

comb = []
for i in range(1, len(alist)+1):
    c = list((combinations(alist, i)))

    for m in range(len(c)):
        if k == sum(c[m]):
            comb.append(c[m])

count = len(comb[0])
for i in range(len(comb)):
    if len(comb[i+1]) <= count:
        count = len(comb[i+1])

print(count)
# --> 런타임 오류

-> 런타임 오류로 실패하였다.

- 정답 코드💻

n, k = map(int, input().split())

alist = []
for i in range(n):
    alist.append(int(input()))

count = 0
alist.sort(reverse=True) #내림차순 정렬

for i in alist:
    if k == 0:
        break
    count += k // i
    k %= i

print(count)

- 비교 분석📖

아예 다른 방향으로 생각했던 것 같다. 지난 시간 풀었던 문제와 비슷한 느낌인 것 같다. 인터넷에서 여러 정답 코드를 보았고, 그것들을 바탕으로 다시 작성하였다. 동전을 내림차순으로 정렬해 큰 수부터 주어진 K값에서 나누다보면 동전 개수의 최소값을 구할 수 있다.

• 헷갈렸던 문법 : 여러 줄을 한 번에 입력받기 -> 성공함
• 헷갈렸던 부분 : 큰 수부터 내림차순으로 나누어 동전 개수의 최소값을 구하는 원리

---

📝문제3. 백준 2839번

- 문제

https://www.acmicpc.net/problem/2839
상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다.

상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수 있다.

상근이가 설탕을 정확하게 N킬로그램 배달해야 할 때, 봉지 몇 개를 가져가면 되는지 그 수를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 N이 주어진다. (3 ≤ N ≤ 5000)

출력
상근이가 배달하는 봉지의 최소 개수를 출력한다. 만약, 정확하게 N킬로그램을 만들 수 없다면 -1을 출력한다.

예제 입력 1 : 18
예제 출력 1 : 4

예제 입력 2 : 4
예제 출력 2 : -1

예제 입력 3 : 6
예제 출력 3 : 2

예제 입력 4 : 9
예제 출력 4 : 3

예제 입력 5 : 11
예제 출력 5 : 3

- 나의 코드💻

n = int(input())

k = n // 5
count = 0
q = 0

if n < 5:
    if n == 3:
        count = 1
    else:
        count = -1


elif n >= 5:
    if n % 5 == 0:
        count = k
    else:
        if k % 3 == 0:
            count = k//3 + k
        elif n % 3 == 0:
            count = n // 3
        else:
            for i in range(1, (n // 5)+1):
                q = n - 5*i
                if q % 3 == 0:
                    count = n // 3 + n // 5
                else:
                    count = -1

print(count)

-> 부끄럽지만, 계속해서 예외를 처리하다 보니 이런 말도 안되는 코드가 나왔다. 입출력 예시1을 성공하니 입출력예시 2가 틀렸고, 이를 수정하니 입출력 예시 3이 틀렸고,, 이를 수정하니,,, 자꾸 틀려서 계속 보완하다보니 엉망진창이 되었다..

- 정답 코드💻

n = int(input())
count = 0

while n >= 0:
    if n % 5 == 0:  # 만일 n이 5의 배수라면
        count += n // 5
        break
    n -= 3
    count += 1  # 5의 배수가 될 때까지 n에서 3을 빼고, count는 1 증가시킨다(3kg 한봉지)
    
# while문이 거짓으로 판정되는 경우
# 즉, count가 0이 될 때까지 5의 배수로 나누어 떨어지지 않는 경우
else: 
    count = -1

print(count)

참고 : https://ooyoung.tistory.com/81
이 링크로 들어가면 이해가 정말 잘 간다!!

- 비교 분석📖

내가 작성한 코드 마지막 부분의 for i in range 구문에서 구현하고 싶던 것이 바로 이런 방법이었는데.. 너무 간결하고 보기 좋게 구현할 수 있다니 놀랐다.

---

문제 출처 : 백준 홈페이지