합병정렬
합병 = '문제를 분할하고, 분할한 문제를 정복하여 합치는 과정'이다.
분할정복 알고리즘을 기반으로 정렬된 방식이라고 볼 수 있다.
합병정렬의 구조상 최대한 작게 문제를 쪼개어 앞의 부분리스트부터 차례대로 합쳐나가기 때문에 안정정렬(Stable Sort) 알고리즘이기도 하다.
시간복잡도 O(nlogn)
전체적인 과정
1. 주어진 리스트를 절반으로 분할하여 부분리스토로 나눈다. (분할)
2. 해당 부분리스트의 길이가 1이 아니라면 1번 과정을 되풀이한다.
3. 인접한 부분리스트끼리 정렬하여 합친다. (정복)
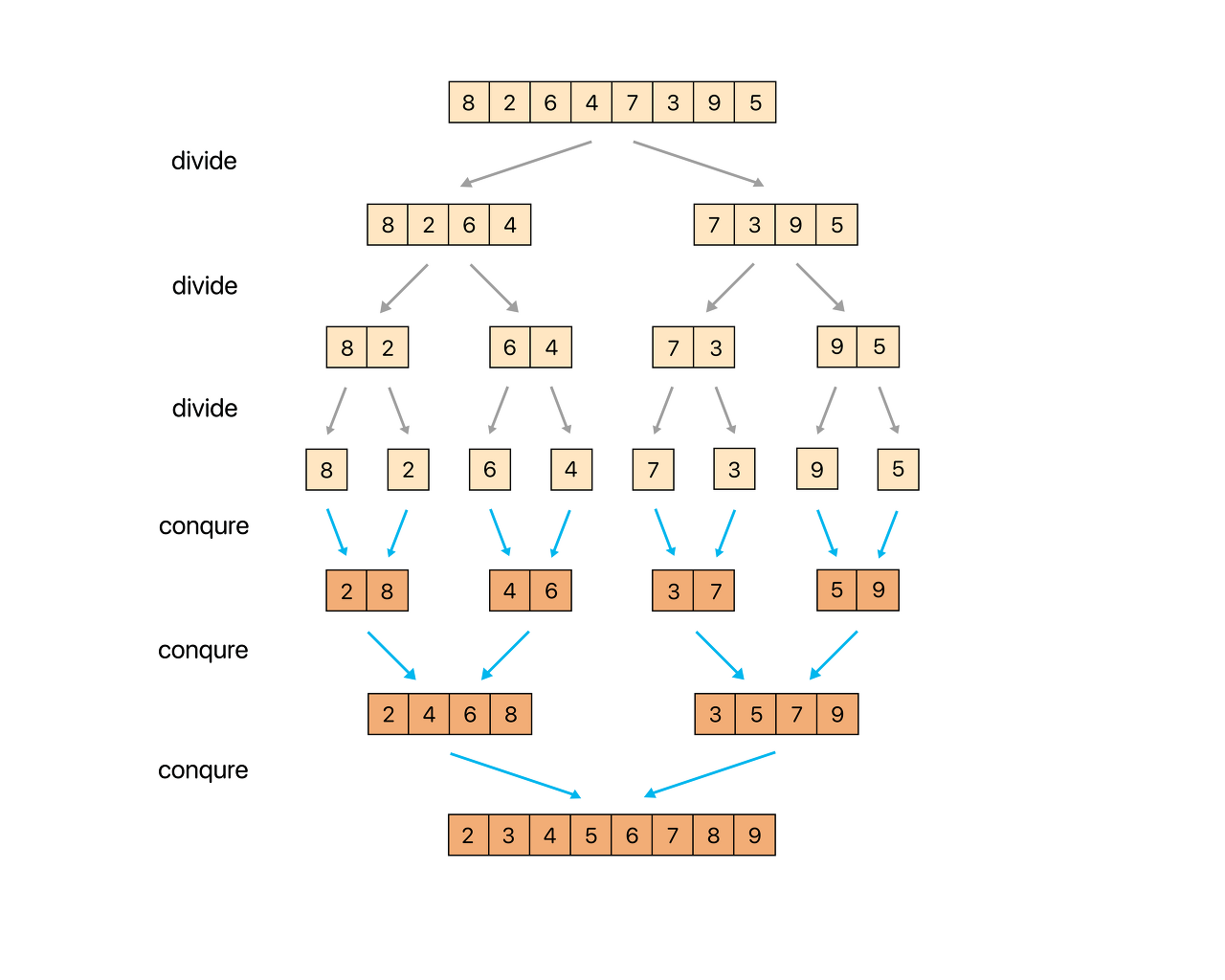
각각 부분리스트는 정렬된 상태여야 하는 점이다.
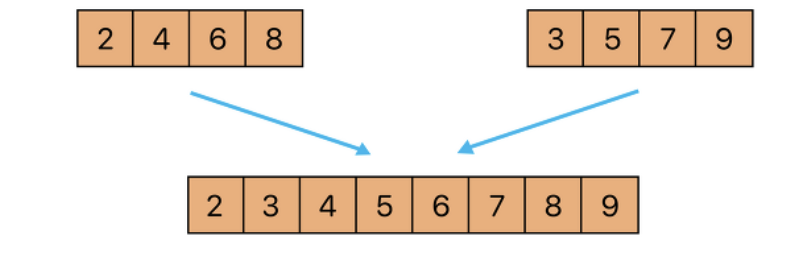
결국적으로 마지막에는 두 부분리스트를 순차적으로 비교하여 정렬한다.
package 정렬;
public class 합병정렬 {
public static void main(String[] args){
int[] arr={6,4,2,5,3,7,8,1};
sort(arr,0,arr.length);
printArray(arr);
}
public static void printArray(int[] arr){
for(int i=0;i<arr.length;i++){
System.out.print(arr[i]+" ");
}
System.out.println();
}
public static void sort(int[] arr,int left,int right){
if(right-left<2){
return;
}
int mid=(left+right)/2;
sort(arr,0,mid);//쪼개는 과정
sort(arr,mid,right);
merge(arr,left,mid,right);
}
public static void merge(int[] arr,int left,int mid,int right){
int[] temp=new int[right-left];//임시 배열 선언
int index=0, l=left,r=mid;//index와 처음 위치 끝 위치 변수
while(l<mid&&r<right){
if(arr[l]<arr[r]){
temp[index]=arr[l];
index++;
l++;
}else{
temp[index]=arr[r];
index++;
r++;
}
}
//순차적으로 비교하면 나머지 부분 리스트가 남는다. 이걸 집어넣기 위한 코드
while(l<mid){
temp[index]=arr[l];
index++;
l++;
}
while(r<right){
temp[index]=arr[r];
index++;
r++;
}
for(int i=left;i<right;i++){
arr[i]=temp[i-left];
}
}
}
https://www.daleseo.com/sort-merge/
https://yunmap.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Java%EB%A1%9C-%EA%B5%AC%ED%98%84%ED%95%98%EB%8A%94-%EC%89%AC%EC%9A%B4-Merge-Sort-%EB%B3%91%ED%95%A9-%EC%A0%95%EB%A0%AC-%ED%95%A9%EB%B3%91-%EC%A0%95%EB%A0%AC
퀵정렬
하나의 리스트를 피qjt을 기준으로 두 개의 부분리스트로 나누어 하나는 피벗보다 작은 값들의 부분리스트, 다른 하나는 피벗보다 큰 값들의 부분리스트로 정렬한 다음, 각 부분리스트에 대해 다시 위 처럼 재귀적으로 수행하여 정렬하는 방법이다.
합병정렬과 다른점은 합병정렬의 경우 절반으로 나누어 분할정복하고, 퀵정렬은 피벗을 기준으로 나누기 때문에 비균등하게 나뉘어 정복한다는 점이다.
서로 떨어진 원소끼리 교환이 일어나기 때문에 불안정 정렬 알고리즘이다.
시간복잡도는 평균 O(nlogn) 최악은 O(N^)
피벗을 선택하는 기준은 3가지이다. 왼쪽, 중앙, 오른쪽
선택함에 따라 코드가 약간 달라질 수 있지만 모두 '피벗'을 설정하고 피벗을 기준으로 왼쪽 오른쪽 부분리스트를 만드는 과정은 같다. 이를 파티셔닝 과정이라고 한다.
피벗을 왼쪽으로 선택하는것이 이해하기 쉽기 때문에 왼쪽 선택 방식으로 구현하겠다.
- 피벗을 하나 선택한다(왼쪽, 중앙, 오른쪽 자유롭게)
- 피벗을 기준으로 왼쪽에서는 피벗보다 큰 값을 찾고, 오른쪽에서는 피벗보다 작은 값을 찾는다.
- 양 방향에서 찾았다면 두 원소를 교환한다.
- 왼쪽 탐색 위치가 오른쪽 탐색위치 보다 작다면 다시 2번부터 반복한다. 둘의 위치가 엇갈렸다면 5번으로
- 엇갈린 기점을 기준으로 두 개의 부분리스트로 나누어 1번으로 돌아가 해당 부분리스트의 길이가 1이 아닐 때 까지 1번 과정을 반복한다(분할)
- 결국 낱게로 나뉘게 되어있고 다 분할하면 인접한 부분리스트끼리 합친다(정복)
package 정렬;
public class 퀵정렬 {
private static void sort(int[] arr,int left,int right){
if(left>=right) return;
int pivot=partition(arr,left,right);
sort(arr,left,pivot-1);
sort(arr,pivot+1,right);
}
private static int partition(int[] arr,int left,int right){
int l=left;
int r=right;
int pivot=arr[left];
while(l<r){
while(arr[r]>pivot&&l<r){
r--;
}
while(arr[l]<=pivot&&l<r){
l++;
}
swap(arr,l,r);
}
swap(arr,left,l);//가장 왼쪽에 있는 원소를 기준으로 나눴기 때문에 현재 l값에 left값 집어넣음
return l;
}
private static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
public static void main(String[] args) {
int n = 10;
int[] arr = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
sort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
}
}
https://www.daleseo.com/sort-quick/
힙정렬
힙정렬은 '힙자료구조'를 기반으로 한다.
힙은 '최대힙'과 '최소힙' 두 종류가 있다.
최대힙이란, 각 노드의 값이 해당 child의 값보다 크거나 같은 완전 이진 트리를 말한다.
최소힙이란, 각 노드의 값이 해당 childe의 값보다 작거나 같은 완전 이진 트리이다.
말 그래도 최대힙의 root는 제일 큰 값을 가지기 때문에, 최대값을 찾는데 소요되는 시간은 O(1)이다. 루트 노드에서 최대값을 삭제하면 빈 루트노드를 다른 노드가 채워줘야한다.
이 과정에서 heap은 맨 마지막 노드를 루트 노드로 대체한 후, heapify 과정을 거쳐 heap 구조를 유지한다.
힙의 경우는 완전 정렬 상태가 아니고 느슨한 정렬 상태이다. 왜냐면 모든 노드가 정렬된채 유지되는것이 아닌 부모 노드가 자식노드보다 항상 큰값이라는 조건만 만족하기 때문이다.
말그대로, 형제간의 우선순위는 고려하지 않는다
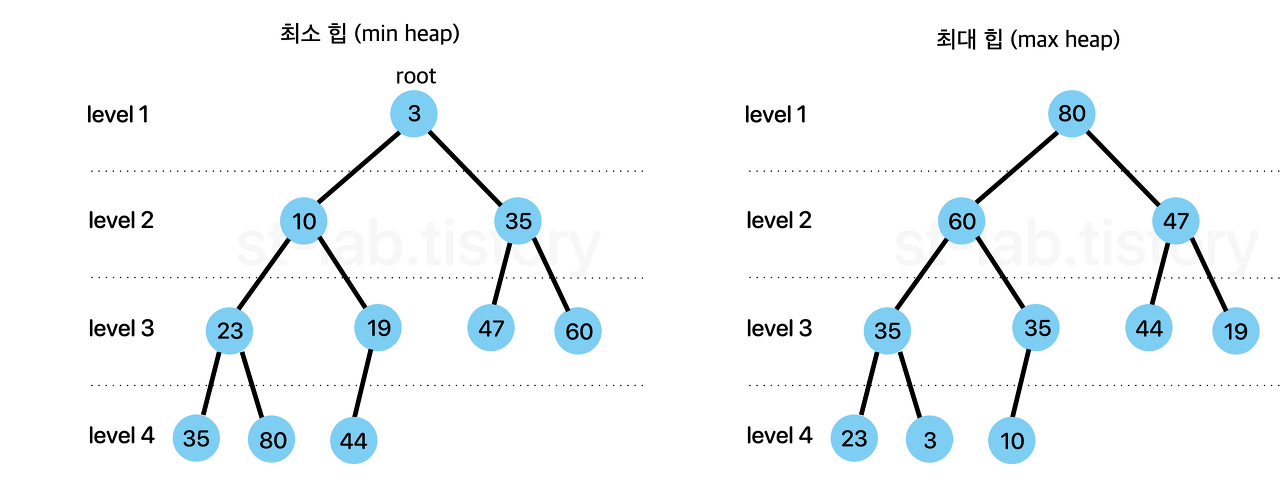
최소 힙 : 부모 노드의 값(key 값) ≤ 자식 노드의 값(key 값)
최대 힙 : 부모 노드의 값(key 값) ≥ 자식 노드의 값(key 값)
heap의 자료구조는 어떻게 구현할 수 있을까?
바로 배열을 이용하는것이다.
힙은 이러한 규칙을 가진다.
왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 x 2 + 1
오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 x 2 + 2
부모 노드 인덱스 = (자식노드 인덱스 - 1) / 2
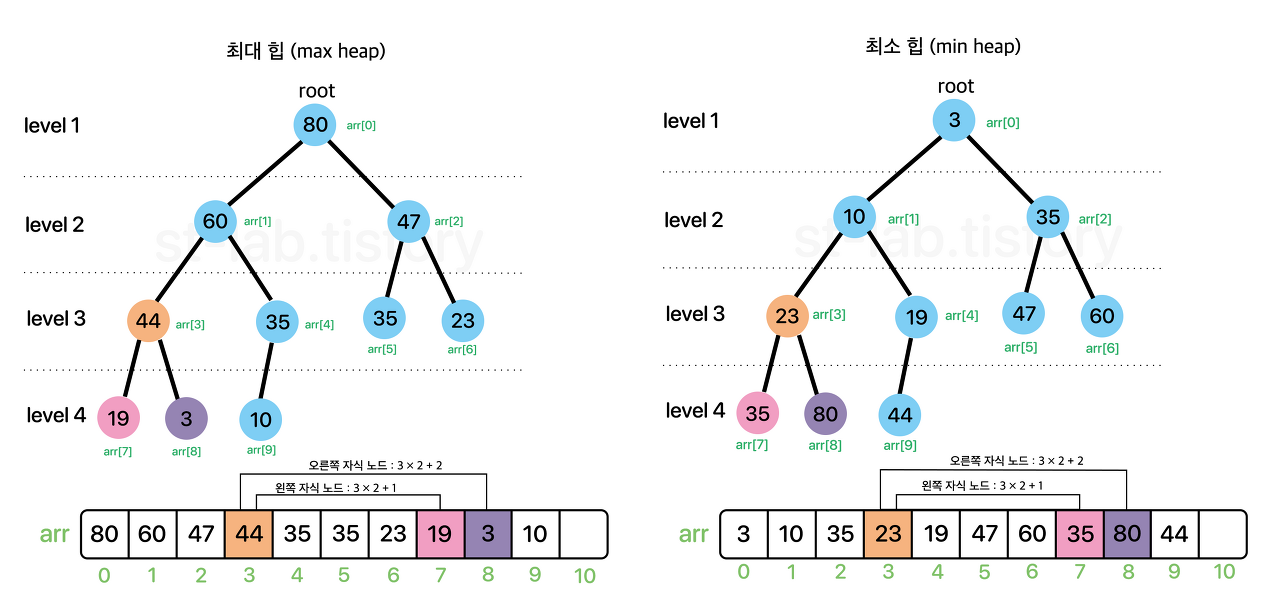
자바의 경우 우선순위큐가 힙자료구조를 기반으로 구현되었다.
그렇기 때문에 자바에서 힙정렬을 이용하고자 하면 우선순위 큐를 사용하면 된다.
package 정렬;
import java.util.*;
public class 힙정렬{
public static void main(String[] args){
int n = 10;
int[] arr = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
PriorityQueue<Integer> pq=new PriorityQueue<Integer>();
for(int i=0;i<n;i++){
pq.add(arr[i]);
}
for(int i=0;i<n;i++){
System.out.print(pq.poll()+" ");
}
}
}
위와 같이 정렬한다면 추가적인 메모리 pq가 필요하다.
만약 heap을 직접 구현하여 추가적인 메모리 없이 힙정렬을 구현한다면 어떻게 될까?
우선 힙 자료구조를 구현해야한다. 힙 자료구조는 이전 배열을 이용하여 구현한다고 이야기 했다.
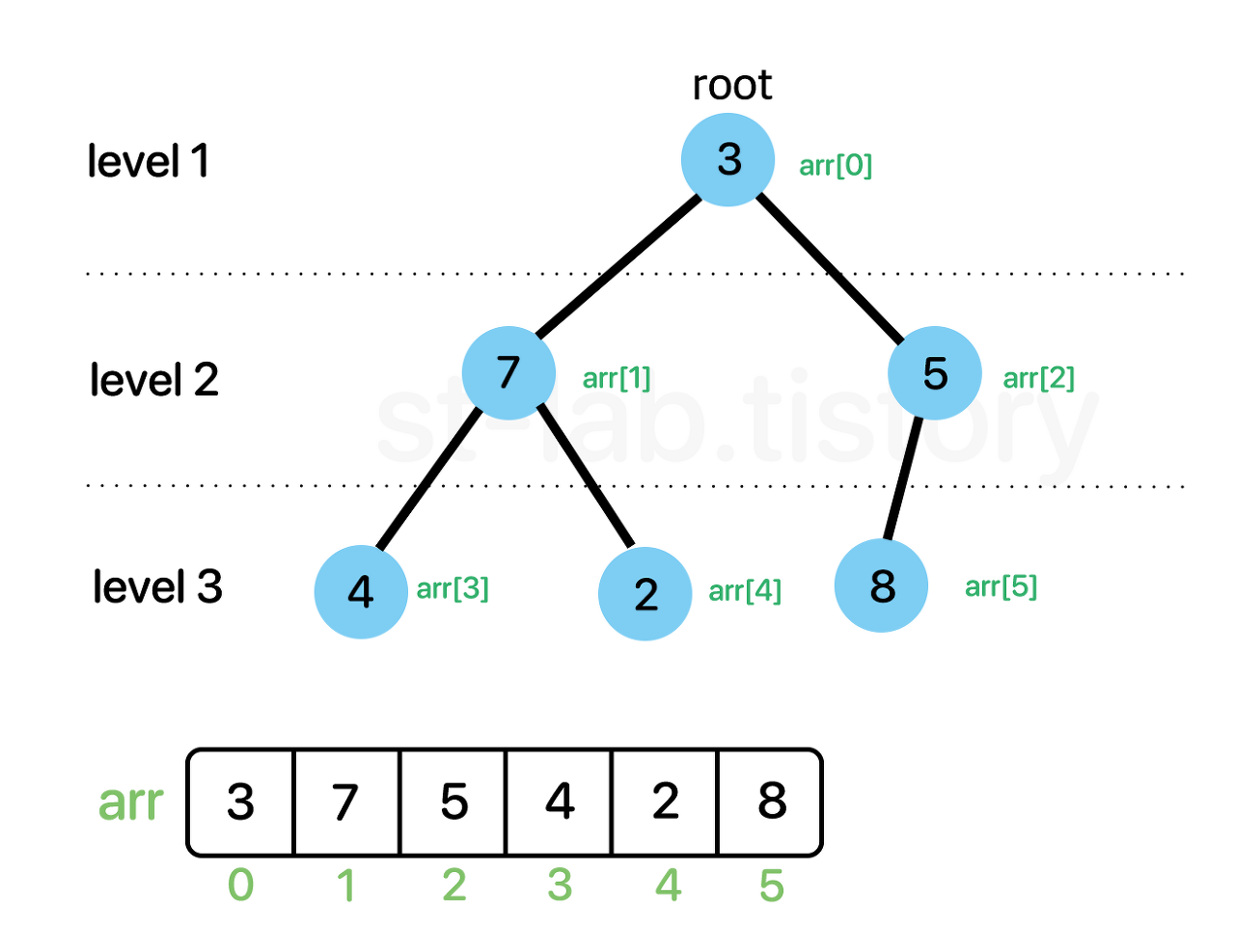
다음은 아직 힙 자료구조가 아닌 배열이다. 위 상태를 최대힙 조건을 만족하도록 구성해보겠다.
- 최대힙 만들기
추가적인 메모리 공간을 생성하지 않고 원본 배열안에서 정렬하기 위해서는 가장 작은 서브트리에서 순차적으로 진행하는 것이다.

위와 같이 힙을 만드는 과정이 heapify이다.
가장 작은 서브 트리부터 진행하기위해 배열의 가장 마지막 값인 8(index 5)을 선택한다. 그럼 왼쪽자식트리 공식에 맞춰 자식 노드는 5(index2)가 선택된다. 두개의 값을 비교해서 swap하면 된다.
private static int getParent(int child){
return (child-1)/2;
}
private static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
private static void heapify(int[] arr,int parentIndex,int lastIndex){
int leftChildIndex=2*parentIndex+1;
int rightChildIndex=2*parentIndex+2;
int max=parentIndex;
if(leftChildIndex<lastIndex&&arr[max]<arr[leftChildIndex]){
max=leftChildIndex;
}
if(rightChildIndex<lastIndex&&arr[max]<arr[rightChildIndex]){
max=rightChildIndex;
}
if(parentIndex!=max){
swap(arr,max,parentIndex);
heapify(arr,max,lastIndex);
}
}최대힙을 구성했다면 최대힙을 이용하여 정렬을 해야한다.
package 정렬;
import java.util.*;
public class 힙정렬{
private static int getParent(int child){
return (child-1)/2;
}
private static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
private static void heapify(int[] arr,int parentIndex,int lastIndex){
int leftChildIndex;
int rightChildIndex;
int max;
while(2*parentIndex+1<=lastIndex) {//왼쪽 자식 노드와 last비교 왜 왼쪽 자식노드 부터? 오른쪽 자식부터 비교했다가
//오른쪽 자식 없음 왼쪽 검사 못함
leftChildIndex=2*parentIndex+1;
rightChildIndex=2*parentIndex+2;
max=parentIndex;//최대값이 부모값이라 가정
if (arr[max] < arr[leftChildIndex]) {//왼쪽이 더 크면 바꿈
max = leftChildIndex;
}
if (rightChildIndex <= lastIndex && arr[max] < arr[rightChildIndex]) {//오른쪽이 더 크면 바꿈
max = rightChildIndex;
}
if (parentIndex != max) {//max값이 부모값이 아니라는건 자식노드값이 더 크다는거
swap(arr, max, parentIndex);//바꿔줌
parentIndex=max;//부모값에 max넣어줌
}else return;
}
}
public static void heapSort(int[] arr){
int size=arr.length;
if(size<2){
return;
}
int parentIndex=getParent(size-1);//가장 마지막 노드 부모 인덱스 찾기
for(int i=parentIndex;i>=0;i--){//가장 마지막 노드 부모 인덱스부터 뒤에있는 부모 인덱스 가져오기
heapify(arr,i,size-1);
}
for(int i=size-1;i>0;i--){
swap(arr,0,i);//정렬하기 위해 최대값 빼오고 마지막 노드 값을 루느 노드로 바꿔줌
heapify(arr,0,i-1);//최대힙으로 구성
}
}
public static void main(String[] args){
int n = 10;
int[] arr = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
PriorityQueue<Integer> pq=new PriorityQueue<Integer>();
for(int i=0;i<n;i++){
pq.add(arr[i]);
}
for(int i=0;i<n;i++){
System.out.print(pq.poll()+" ");
}
System.out.println();
int[] arr2 = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
heapSort(arr2);
for(int i=0;i<n;i++){
System.out.print(arr2[i]+" ");
}
}
}
힙 정렬의 장점 및 단점
[장점]
-
최악의 경우에도 O(NlogN) 으로 유지가 된다.
-
힙의 특징상 부분 정렬을 할 때 효과가 좋다.
[단점]
-
일반적인 O(NlogN) 정렬 알고리즘에 비해 성능은 약간 떨어진다.
-
한 번 최대힙을 만들면서 불안정 정렬 상태에서 최댓값만 갖고 정렬을 하기 때문에 안정정렬이 아니다.
