다이나믹 프로그래밍

• 다이나믹 프로그래밍은 동적 계획법이라고도 부릅니다.
• 다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법입니다.
• 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 합니다.
• 다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(탑다운과 보텀업)으로 구성됩니다.

다이나믹 프로그래밍의 조건

1. 최적 부분 구조 ( Optimal Substructure )

• 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있습니다.

2. 중복되는 부분 문제 ( Overlapping Subproblem )

• 동일한 작은 문제를 반복적으로 해결해야 합니다.

  피보나치 수열

  

피보나치 수열 시간 복잡도 분석

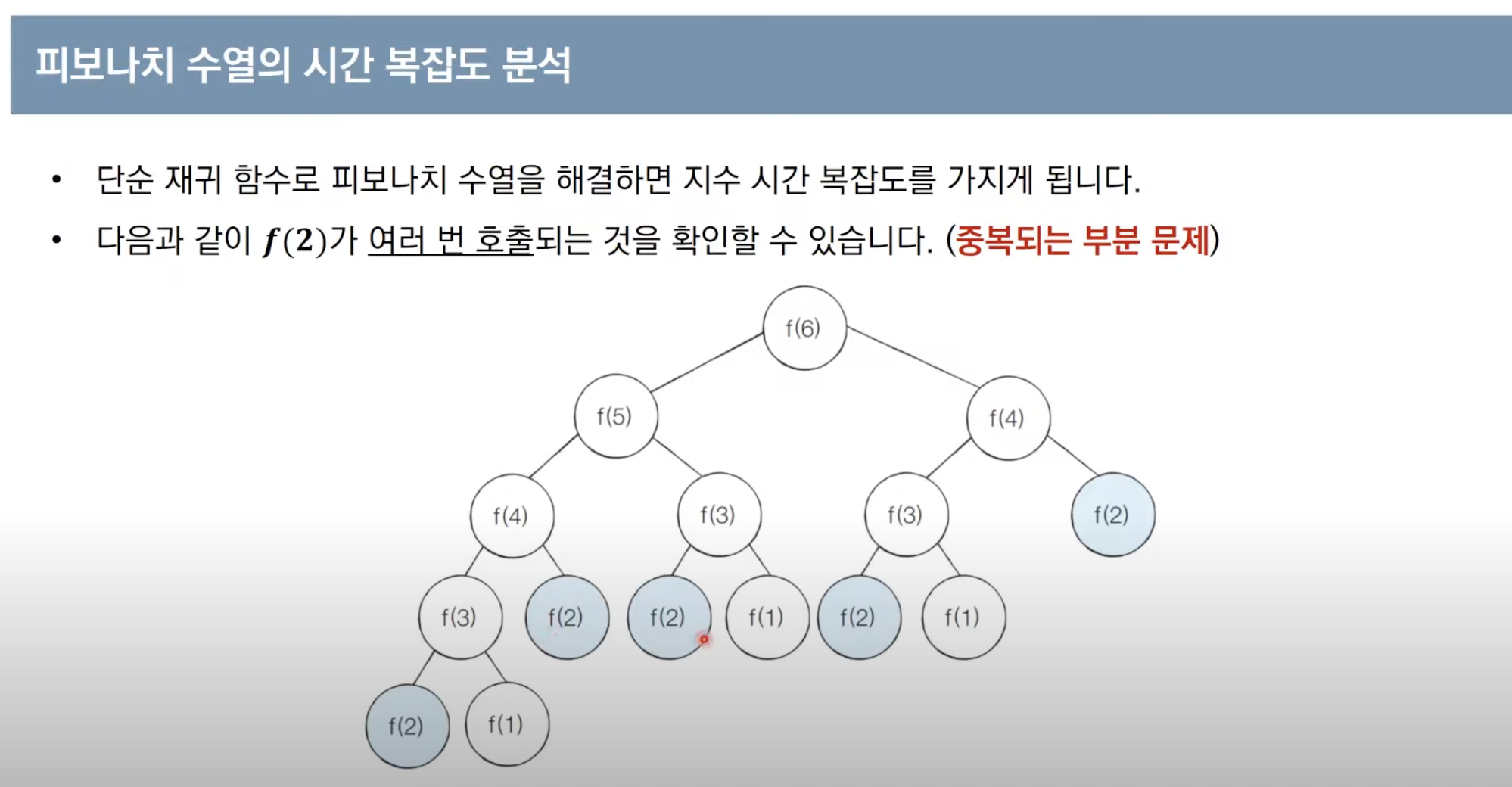
중복되는 문제가 있기 때문에
시간 복잡도는 O(2^n)이다. -> 효율적이지 않음

피보나치 수열의 효율적인 해법 -> 다이나믹 프로그래밍

메모이제이션

• 메모이제이션은 다이나믹 프로그래밍을 구현하는 방법 중 하나이다.
• 한 번 계산한 결과를 메모리 공간에 메모하는 기업
  -> 캐싱이라고도 한다.

탑다운 vs 보텀업

탑다운

d = [0] * 100

def fibo(x):
   print('f(' + str(x) + ')', end=' ')
   if x == 1 or x == 2:
       return 1
   if d[x] != 0:
       return d[x]
   d[x] = fibo(x - 1) + fibo(x - 2)
   return d[x]

fibo(6)

버텀업

# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100

# 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1
d[2] = 1
n = 99

# 피보나치 함수(Fibonacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for i in range(3, n + 1):
    d[i] = d[i - 1] + d[i - 2]

print(d[n])

-> 시간복잡도 O(N)

다이나믹 프로그래밍 vs 분할 정복

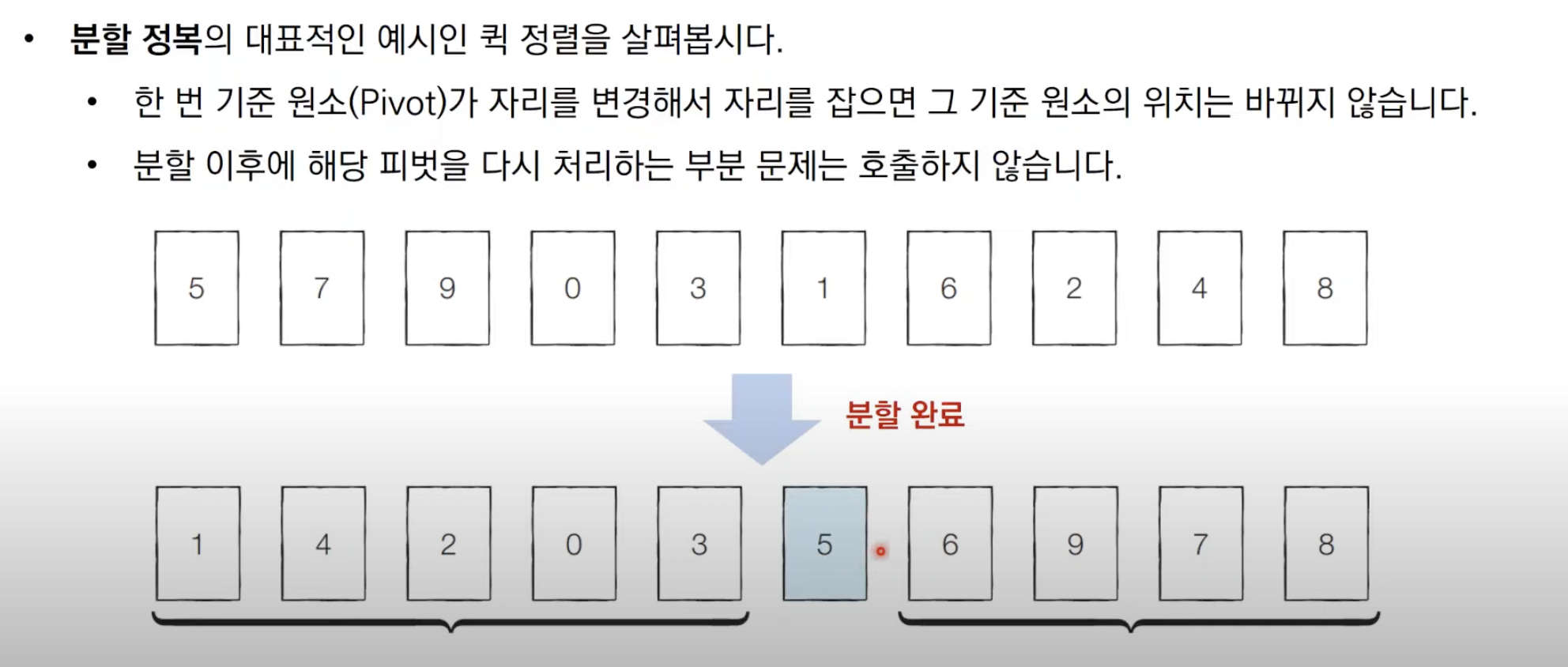
다이나믹 프로그래밍 문제에 접근하는 방법