[알고리즘] 순열, 조합, 부분집합

Jifrozen·2022년 10월 11일

기초 다지기

목록 보기

11/29

순열

n개의 원소에서 순서를 생각하며 r개의 원소를 선택하는 방법이다.
입력 : [1, 2, 3]
출력 : [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1], [3, 1, 2]

1. swap

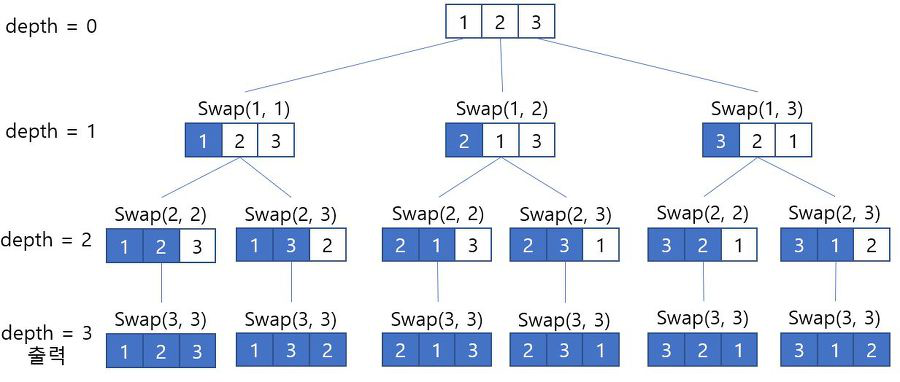
swap 함수를 만들어서 배열들의 값을 직접 바꾸는 방법이다.

배열의 첫 값부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap 한다.

depth 를 기준 인덱스로 하여 depth 보다 인덱스가 작은 값들은 그대로 고정하고

depth 보다 인덱스가 큰 값들만 가지고 다시 swap 을 진행한다.

public void swap(int idx, int idx2, int[] arr){
		int tmp = arr[idx];
		arr[idx2] = arr[idx];
		arr[idx2] = tmp;
	}

	public void permutation(int depth,int r,int[] arr){
		if(depth==r){
			for(int i=0;i<r;i++){
				System.out.print(arr[i]+" ");
			}
			return;
		}

		for(int i=depth;i<arr.length;i++){
			swap(depth,i,arr);
			permutation(depth+1,r,arr);
			swap(depth,i,arr);
		}
	}

2. Visited 배열을 이용한 순열 (DFS)

1번과 달리 사전식으로 순열을 구현할 수 있습니다.

변수 설명

arr : r 개를 뽑기 위한 n 개의 값
output : 뽑힌 r 개의 값
visited : 중복해서 뽑지 않기 위해 체크하는 값

위 3개의 값이 포인트입니다.

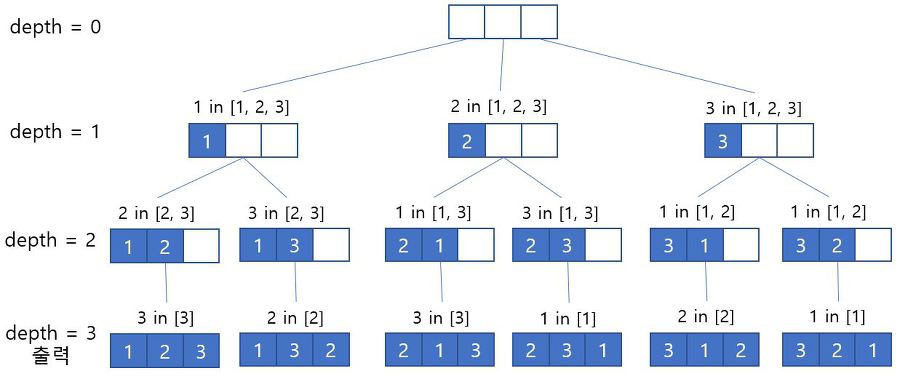
DFS를 돌면서 모든 인덱스를 방문하여 output 에 값을 넣습니다.

이미 들어간 값은 visited 값을 true 로 바꾸어 중복하여 넣지 않도록 합니다.

depth 값은 output 에 들어간 숫자의 길이라고 생각하시면 됩니다.

depth 의 값이 r 만큼 되면 output 에 들어있는 값을 출력하면 됩니다.

// 순서를 지키면서 n 개중에서 r 개를 뽑는 경우
// 사용 예시: perm(arr, output, visited, 0, n, 3);
static void perm(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {
    if (depth == r) {
        print(output, r);
        return;
    }
 
    for (int i=0; i<n; i++) {
        if (visited[i] != true) {
            visited[i] = true;
            output[depth] = arr[i];
            perm(arr, output, visited, depth + 1, n, r);       
            output[depth] = 0; // 이 줄은 없어도 됨
            visited[i] = false;;
        }
    }
}

조합

순열과 같이 n개의 원소에서 r개의 원소를 선택하지만, 원소를 뽑는 순서는 고려하지 않는다.
즉, 다른 두 경우의 수가 있을 때, 두 경우의 수의 내용(뽑은 원소)가 같다면 같은 경우의 수로 생각한다.
입력 : [1, 2, 3]
출력 : [1, 2], [1, 3], [2, 3]

1. 백트래킹

start 변수는 기준입니다.

start 인덱스를 기준으로 start 보다 작으면 뽑을 후보에서 제외, start 보다 크면 뽑을 후보가 됩니다.

예를 들어 [1, 2, 3] 배열이 있고 start 가 0 부터 시작합니다.

함수에 들어오면 먼저 i 가 start 부터 시작하는 for 문에 들어갑니다.

만약 0 인덱스인 1을 뽑는다면 visited[i] 는 true 가 되고 뽑지 않는다면 visited[i] 는 false 입니다.

1을 선택한 경우와 선택하지 않은 경우 둘 다 봐야합니다.

하지만 더이상 1은 고려 대상이 아니기 때문에 다음 for 문은 무조건 i+1 부터 시작해주어야 합니다.

 // 배열 출력
    static void print(int[] arr, boolean[] visited) {
        for(int i = 0; i < arr.length; i++) {
            if(visited[i] == true)
                System.out.print(arr[i] + " ");
        }
        System.out.println();
    }
// 백트래킹 사용
// 사용 예시 : combination(arr, visited, 0, n, r)
static void combination(int[] arr, boolean[] visited, int start, int n, int r) {
    if(r == 0) {
        print(arr, visited, n);
        return;
    } 

    for(int i=start; i<n; i++) {
        visited[i] = true;
        combination(arr, visited, i + 1, n, r - 1);
        visited[i] = false;
    }
}

2. 재귀

depth 변수를 사용합니다.

depth 변수는 현재 인덱스라고 생각하면 됩니다.

현재 인덱스를 뽑는다면 visited[depth] = true

뽑지 않는다면 visited[depth] = false

이렇게 진행하면 됩니다.

역시 마찬가지로 뽑은 경우와 뽑지 않은 경우 모두 봐야하고, 그 때 이전에 본 값들은 더이상 고려 대상이 아니기 때문에 depth 은 무조건 1 씩 증가합니다.

depth == n 이 되면 모든 인덱스를 다 보았으므로 재귀를 종료합니다.

// 재귀 사용
// 사용 예시 : comb(arr, visited, 0, n, r)
static void comb(int[] arr, boolean[] visited, int depth, int n, int r) {
    if (r == 0) {
        print(arr, visited, n);
        return;
    }

    if (depth == n) {
        return;
    }

    visited[depth] = true;
    comb(arr, visited, depth + 1, n, r - 1);

    visited[depth] = false;
    comb(arr, visited, depth + 1, n, r);
}

부분집합

입력 : [1, 2, 3]
출력 : [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]

조합에서는 길이가 r 일 때를 구하기 위해 여러가지 조건을 걸었지만 부분집합에서는 필요없습니다.
현재 인덱스를 포함하는 경우
현재 인덱스를 포함하지 않는 경우
두 가지로 경우에 대해서 모두 확인한 후에 현재 인덱스가 n 이 되면 출력합니다.

 static void powerSet(int[] arr, boolean[] visited, int n, int idx) {
    if(idx == n) {
        print(arr, visited, n);
        return;
    }
 
    visited[idx] = false;
    powerSet(arr, visited, n, idx + 1);
 
    visited[idx] = true;
    powerSet(arr, visited, n, idx + 1);
}

비트연산에 대한 이해가 있다면 구현할 수 있습니다.

n 이 3이라고 할 때 1 << n 은 1000(2) 입니다.

첫번째 for 문에서 i 는 1 << n 전까지 증가하니까 111(2) 까지 증가합니다.

즉 i 는

000
001
010
011
100
101
110
111
이렇게 증가합니다.

한번 쓱 보니 비트 자체만으로도 부분 집합이 형성되었습니다.

j 를 통해서

001
010
100
위 숫자들과 AND 연산을 통해서 1 인 비트들을 인덱스처럼 사용할 수 있습니다.

static void bit(int[] arr, int n) {
    for(int i=0; i < 1<<n; i++) {
        for(int j=0; j<n; j++) {
            if((i & 1<<j) != 0) 
                System.out.print(arr[j] + " ");
        }
        System.out.println();
    }
}