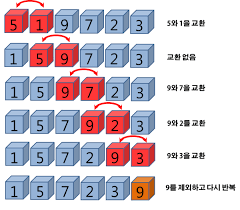
버블 정렬

두 인접한 데이터의 크기를 비교해 정렬하는 방법
시간 복잡도 - swap 여부를 판단 할 수 있는 변수를 두지 않고 하는 구현의 경우는 O(N2), swap여부를 판단할 수 있는 변수를 둔 경우 O(N)

import java.util.Arrays;

public class 버블정렬 {
	public static void main(String[] args) {
		int n = 10;
		int[] arr = {7, 5, 9, 0, 3, 1, 6, 2, 4, 8};

		Arrays.sort(arr);

		for (int i = 0; i < n - 1; i++) {
			if (arr[i] == arr[i + 1]) {
				System.out.print("D");
				return;
			}
		}

		System.out.print("U");
	}

}

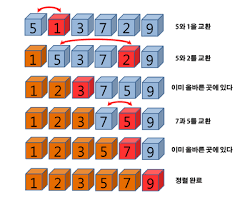
선택 정렬

대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법
시간복잡도 - O(N^)
정렬 된 상태 최선의 경우 O(N)의 시간 복잡도를 갖게 됨

public class 선택정렬 {

    public static void main(String[] args) {

        int n = 10;
        int[] arr = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };

        for (int i = 0; i < n; i++) {
            int min_index = i;
            for (int j = i + 1; j < n; j++) {
                if (arr[min_index] > arr[j]) {
                    min_index = j;
                }
            }
            int temp = arr[i];
            arr[i] = arr[min_index];
            arr[min_index] = temp;
        }

        for (int i = 0; i < n; i++) {
            System.out.print(arr[i] + " ");
        }
    }

}

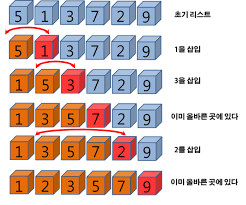
삽입 정렬

이미 정렬된 데이터 범위에 종렬되지 않은 데이터를 적절한 위치에 삽입 시켜 정렬하는 방식
시간 복잡도 - O(N^)

public class 삽입정렬 {
    public static void main(String[] args) {

        int n = 10;
        int[] arr = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };

        for (int i = 1; i < n; i++) {
            for (int j = i; j > 0; j--) {
                if (arr[j] < arr[j - 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j - 1];
                    arr[j - 1] = temp;
                } else
                    break;
            }
        }

        for (int i = 0; i < n; i++) {
            System.out.print(arr[i] + " ");
        }

    }

}