그래프
정점과 간선의 집합, Graph
정점(Vertex)과 간선(Edge)으로 이루어진 자료구조이다.
정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼 수 있다.
이러한 면에서 트리는 그래프의 일종인 셈이다.
하지만 그래프는 트리와는 달리 정점마다 간선이 있을 수도 있고 없을 수도 있으며, 루트노드와 부모와 자식이라는 개념이 존재하지 않는다.
그래프 구현 방법
그래프를 구현하는 방법에는 인접행렬과 인접리스트 방식이 있다. 두 개의 구현방식은 각각의 상반된 장단점을 가지고 있다.
- 인접 행렬 (adjacent matrix) : 그래프의 노드를 2차원 배열로 만든 것 (정방 행렬)
노드들 간에 직접 연결이 되어있으면 1을, 아니면 0을 넣어서 행렬을 완성시킨 것이다.
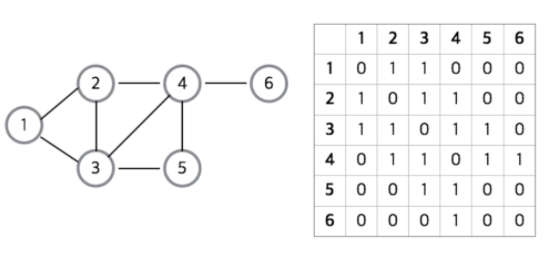
해당하는 위치의 value 값을 통해서 vertex 간의 연결 관계를 O(1) 으로 파악할 수 있다. -> 모든 정점들의 간선 정보가 담겨있기 때문
Edge 개수와는 무관하게 V^2 의 Space Complexity 를 갖는다.-> 모든 정점들의 간선 정보를 담아야하기 때문
Dense graph(밀집 그래프) 를 표현할 때 적절할 방법이다. -> 무조건 V^2 공간을 소모하기 때문에 밀집 그래프를 표현할때 좋음
- 인접 리스트 (adjacent list) : 연결 리스트를 사용하는 방법
주로 정점의 리스트 배열을 만들어 관계를 설정하며 노드들 간에 직접 연결이 되어있으면 해당 노드의 인덱스에 그 노드를 삽입해주면 된다.
즉, 1에는 2와 3이 직접 연결되어 있기 때문에 배열의 1번째 칸에 2와 3을 넣어준다.

정점들의 연결 정보를 탐색할 때 O(n) 시간이면 가능하다.
vertex 의 adjacent list 를 확인해봐야 하므로 vertex 간 연결되어있는지 확인하는데 오래 걸린다. -> (O(E) 시간 소요. E는 간선의 개수)
Space Complexity 는 O(E + V)이다. -> 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
Sparse graph 를 표현하는데 적당한 방법이다.
그래프의 종류
-
무방향 그래프(Undirected Graph)
무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프이다.

-
방향 그래프(Directed Graph)
방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프이다.
간선의 방향으로만 이동할 수 있다.
Degree
Undirected Graph 에서 각 정점(Vertex)에 연결된 Edge 의 개수를 Degree 라 한다. Directed Graph 에서는 간선에 방향성이 존재하기 때문에 Degree 가 두 개로 나뉘게 된다. 각 정점으로부터 나가는 간선의 개수를 Outdegree 라 하고, 들어오는 간선의 개수를 Indegree 라 한다.
-
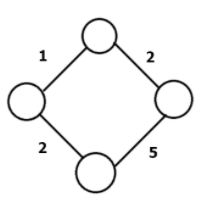
가중치 그래프(Weighted Graph)
가중치 그래프는 간선에 가중치(비용)가 할당된 그래프로, 두 정점을 이동할 때 비용이 드는 그래프이다.
-
연결 그래프(Connected Graph)
무방향 그래프에 있는 모든 정점 쌍에 대해서 항상 경로가 존재하는 그래프
즉, 노드들이 하나도 빠짐없이 간선에 의해 연결되어 있는 그래프로 트리(Tree)가 대표적인 예이다.
-
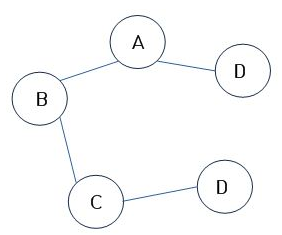
비연결 그래프(Disconnected Graph)
무방향 그래프에서 특정 정점 사이에 경로가 존재하지 않는 그래프
즉, 노드들 중 간선에 의해 연결되어 있지 않은 그래프이다.
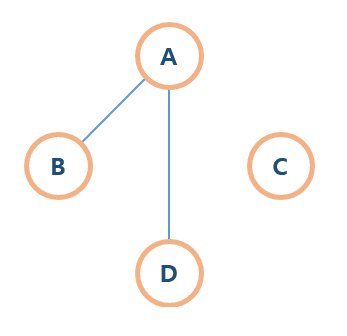
- 완전 그래프(Complete graph)
그래프의 모든 정점이 서로 연결되어 있는 그래프이다. (인접 연결)
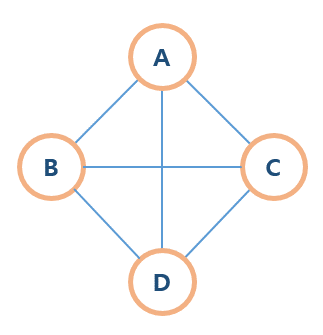
- 순환그래프(Cycle)
단순 경로에서 시작 정점과 도착 정점이 동일한 그래프이다. (A에서 시작-> A에서 끝 가능)
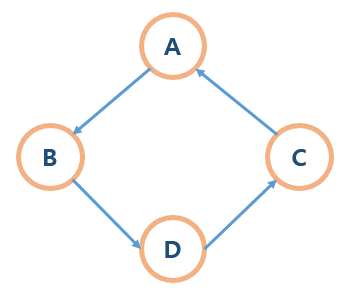
- 비순환그래프(Acyclic Graph)
사이클 그래프를 제외한 그래프로, 사이클이 없는 그래프이다.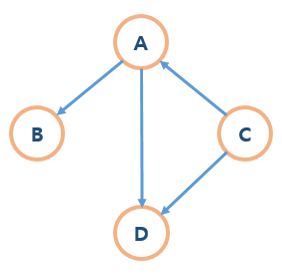
최소 신장트리(Minimum Spanning Tree)
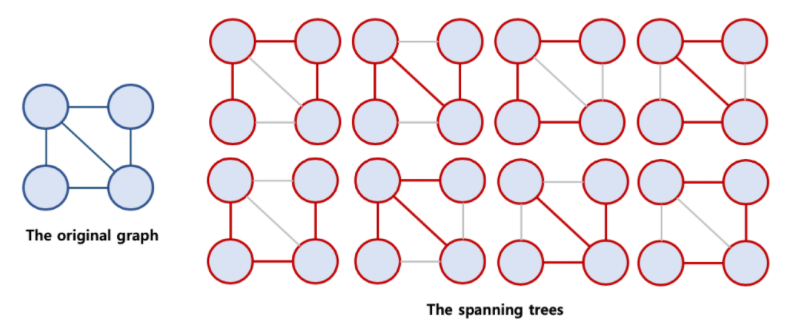
- 신장트리(Spanning Tree)
원래 그래프의 모든 노드가 연결되어 있으면서, 트리의 속성을 만족하는 그래프
트리의 속성을 만족하기 때문에 사이클이 존재하면 안된다.
그래프 G 의 spanning tree 중 edge weight 의 합이 최소인 spanning tree를 말한다.
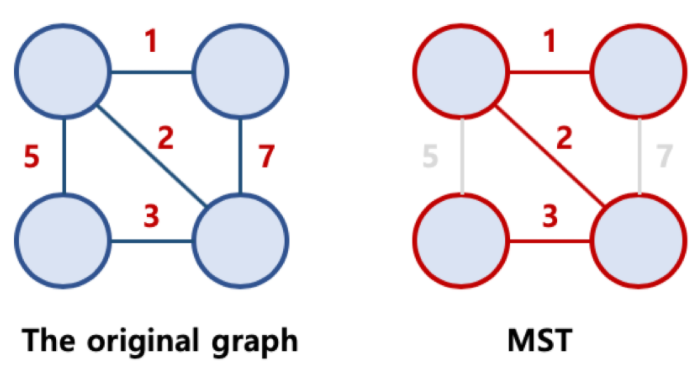
출처 - https://hongcoding.tistory.com/78
https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/DataStructure#graph