1. Dijkstra 알고리즘
알고리즘 개요
목표
특정 시작 지점에서 다른 모든 지점까지의 거리를 구한다
알고리즘 주저리주저리
이 알고리즘에는 현재까지 최단거리가 확정된 노드들의 집합인 Y, 현재까지 계산된 시작 노드로부터의 최단거리를 나타내는 배열인 length가 사용된다. length는 최초에는 시작 노드에서의 거리를 단편적으로 저장하는데, Y 집합에 노드가 추가됨에 따라, "시작 노드에서 -> Y에 속한 노드를 경유하여 -> 각 노드로 가는 최단거리" 를 저장하게 된다.
무슨 말인지, 아래를 읽어보면서 조금씩 더 알아보자.
알고리즘 원리
- 이미 탐색한 노드들의 집합을 Y라고 하자. 처음 Y는 {v1} 뿐이다
- v1을 기준으로 각 노드까지의 최단거리를 저장하는 리스트를 length라고 하자. 이 리스트는 계속해서 갱신된다. 최초의 length 리스트는 [0, 7, 4, 6, 1]이 된다. (바로 갈 수 없는 노드까지의 거리는 무한대로 가정한다)
- length 기준으로 v1에서 가장 가까운 노드를 vnear라고 하자. vnear로 이동하고, 해당 노드를 Y 집합에 포함한다
- 변경된 Y를 기준으로 length 배열을 갱신한다. 이때 length 배열의 변경 식은 다음과 같다.
length 배열에서의 vnear까지의 거리 + vnear에서 각 노드까지의 거리가 원래 length 배열에서의 i까지의 거리보다 작은 경우, 해당 값으로 length를 갱신한다.
(기존의 Y에서 해당 노드로 가는 방법보다, 새로 추가된 vnear를 거쳐 가는 쪽이 더 가까운지 확인하는 과정이다) - Y가 모든 노드를 포함할 때까지 1, 2의 과정을 반복한다.
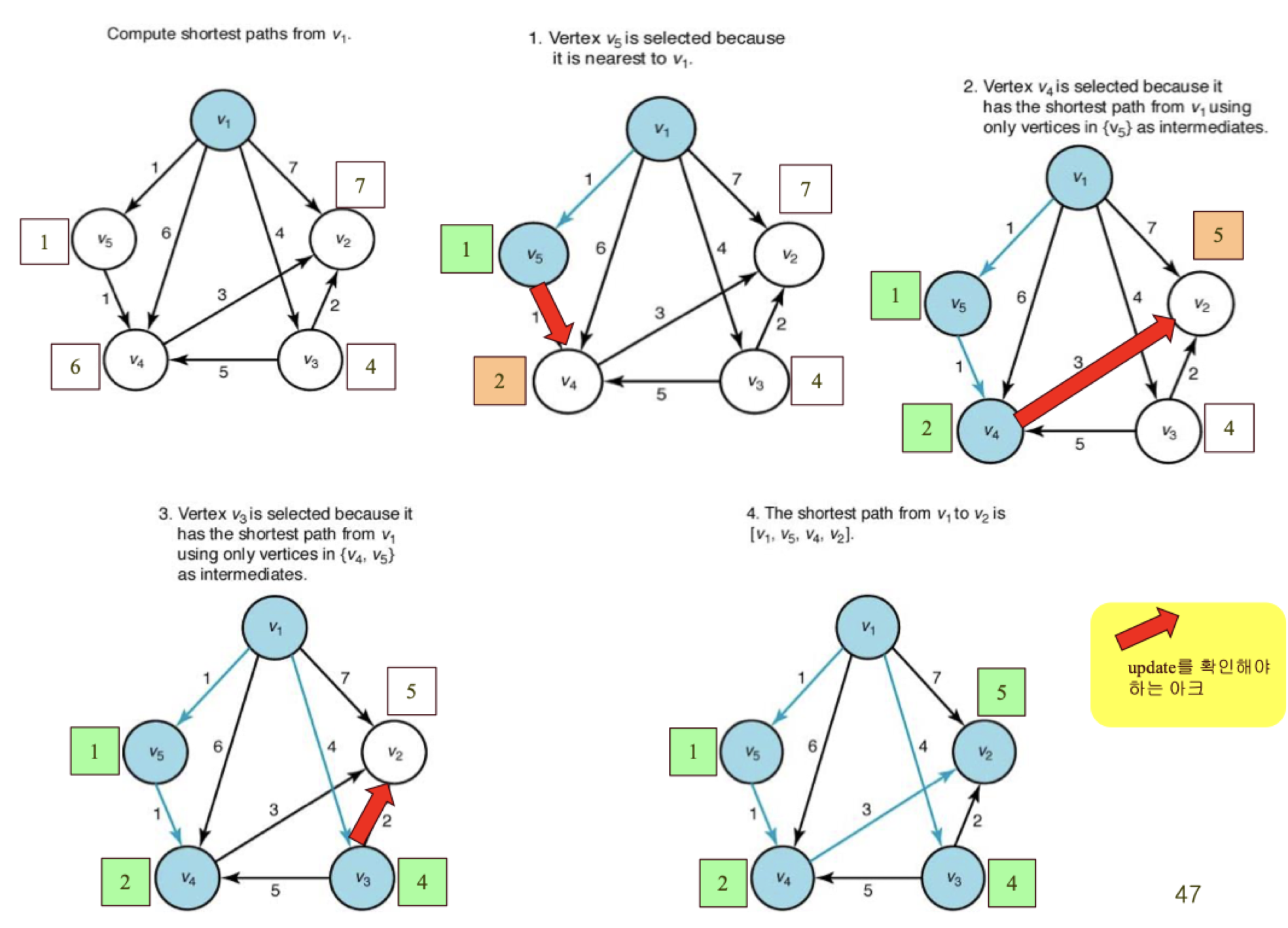
알고리즘 적용
- 최초 Y 집합은 {v1}, length = [0, 7, 4, 6, 1]
- Y 집합에서 가장 가까운 노드인 v5를 Y 집합에 포함한다. Y = {v1, v5}
- Y가 변경되었으므로, 이에 따라 length 배열을 변경한다. 이때 v4까지의 거리는 기존의 6보다, v5를 거쳐가는 방법인 1 + 1 = 2가 더 가까우므로, length를 [0, 7, 4, 2, 1]로 변경한다.
- Y에 없는 노드들 중 가장 가까운 노드는 v4이므로, Y = {v1, v4, v5}가 된다.
- Y가 변경되었으므로, 이에 따라 length 배열을 변경한다. 이때 v2를 보면, v1 -> v4 -> v2 경로의 거리인 2 + 3 = 5가 기존의 7보다 가까우므로, v2의 값을 5로 변경한다. 따라서 length = [0, 5, 4, 2, 1]
- Y에 없는 노드들 중 가장 가까운 노드는 v3이므로, v3를 Y에 포함한다. Y = {v1, v2, v4, v5}.
- Y가 변경되었으므로, 이에 따라 length 배열을 변경한다. 이때 length 배열은 변경되지 않는다.
- Y에 없는 노드들 중 가장 가까운 노드는 v3이므로 (v3 하나만 남아 있었다), v3를 Y에 포함하고 알고리즘을 종료한다.
결론 : v1부터 각 노드까지의 거리 -> [0, 5, 4, 2, 1]
2. Huffman Code (허프만 코드)
허프만 코드란?
허프만 코드는 Prefix 속성을 가지는 코드이다. 이때 Prefix 속성이란, 한 문자의 코드가 다른 문자의 코드의 앞부분이 될 수 없는 성질을 의미한다. 이러한 성질이 필요한 이유는, 어떠한 코드 문자열이 Prefix 속성을 만족해야만 유일한 해석이 존재한다. 코드가 Prefix 속성을 가지지 않는 경우, 같은 코드에 대해 여러 다른 해석이 존재할 수 있게 된다.
이때 어떠한 문자를 효율적으로 코드로 변환하기 위해서는, 코드에서 여러 번 사용되는 문자는 최대한 짧게, 가끔 사용되는 문자에 대해서는 긴 코드를 할당해야 할 것이다, 허프만 코드란, 주어진 조건 하에서 코드의 총 길이는 최대한 짧게, 그러면서도 Prefix 속성을 만족하는 Binary 코드를 말한다.
어떻게 만드는가?
- 문자의 사용 빈도를 기준으로 특정한 Heap을 구축한다.
- Heap에서에 위치에 따라 0,1로 이루어진 코드를 부여한다.
Heap을 어떻게 만드는데요?
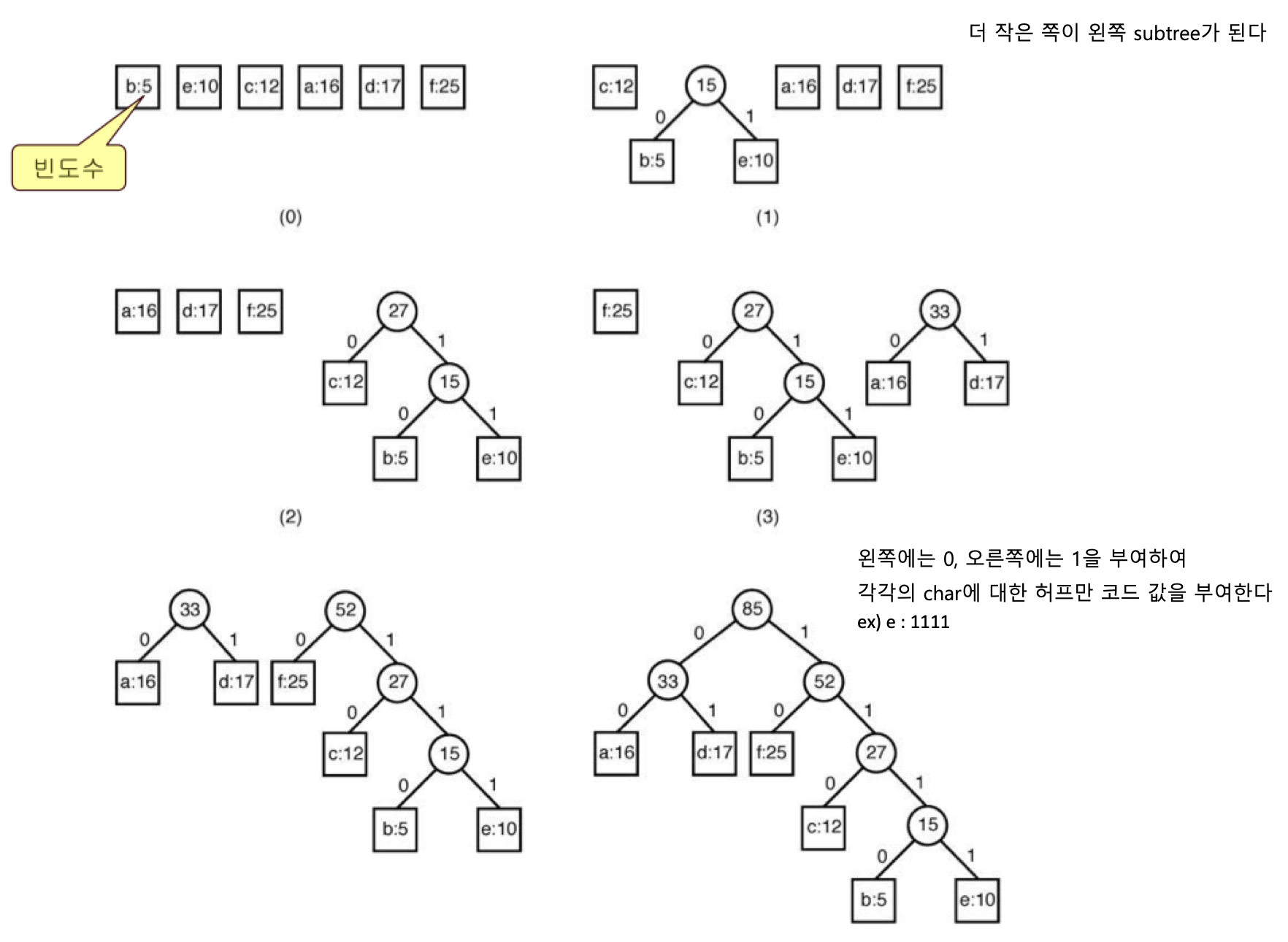
- (문자, 빈도수)를 item으로 가지는 Nodetype을 생각해 보자. 이때 이 Nodetype들의 배열에서, 빈도수가 가장 작은 노드 두 개를 고른다.
- 두 노드를 자식으로 하는 부모 노드를 생성한다. 이때 부모 노드의 문자는 의미가 없고, 빈도수는 두 자식 노드의 합으로 한다. 여기서는 두 자식 노드 중 더 작은 값을 가지는 노드를 왼쪽으로 한다.
- 다시 빈도수가 가장 작은 노드 두 개를 고른다. 이때 앞의 2번 과정을 통해 기존 배열에서 삭제된 두 노드는, 두 노드의 부모 노드 하나로 대체한다 (두 자식 노드를 삭제하고 부모 노드를 추가한다).
- 역시나 두 노드를 자식 노드로 하는 부모 노드를 생성한다.
- 이러한 과정, Tree에 포함되지 않는 노드가 없을 때까지 반복한다.
이러한 과정을 반복하면, 위의 사진과 같은 모양이 만들어지게 된다.
Code는 어떻게 부여하는데요?
아주 단순한데, "왼쪽 자식으로 가면 0, 오른쪽 자식으로 가면 1을 부여한다".
즉 위의 그림에서 e는 Root 기준으로 5번 오른쪽으로 이동하면 되므로 11111이고, d는 왼쪽으로 한 번, 오른쪽으로 한 번 이동하면 되므로 01이 된다.
3. (Fractional) Knapsack Problem (빈틈없이 배낭채우기 문제)
물건마다 특정한 무게와 가격을 가지고 있다고 하자. 또한 우리의 배낭은 물건을 채울 수 있는 최대 무게가 정해져 있다. 이때 목표는 다음과 같다.
배낭의 최대 한도 안에서, 가장 높은 가격을 가지도록 물건을 채우자 (단, 하나의 물건을 나누어서 넣을 수도 있다)
물건을 부분적으로 나누어 넣을 수 있다는 조건이 존재하는 경우, 이 문제를 greedy 알고리즘으로 해결할 수 있다는 사실이 알려져 있다. (이러한 조건이 없는 경우에는, Backtracking 혹은 Branch-and-Bound 알고리즘을 이용한다)
예를 들어 보자. 배낭이 30kg까지 담을 수 있다고 할 때,
item1 : 5kg / 50만원
item2 : 10kg / 60만원
item3 : 20kg / 140만원
이라고 가정하자. 배낭에 가장 높은 가격의 물건을 담기 위해서는 우선 단위 무게당 값어치가 높은 물건부터 최대한 넣고, 더 넣을 수 없는 경우 남은 무게만큼 잘라서 넣으면 된다.
따라서 단위 무게당 가치가 가장 높은 item1을 넣고, 다음으로 item3를 넣은 후, 남은 5kg에 물건을 넣기 위해 item2를 절반 잘라 넣으면 된다. 이렇게 시행하는 경우 총 220만원어치를 넣을 수 있게 된다.
Knapsack Problem (배낭채우기 문제)
물건마다 특정한 무게와 가격을 가지고 있다고 하자. 또한 우리의 배낭은 물건을 채울 수 있는 최대 무게가 정해져 있다. 이때 목표는 다음과 같다.
배낭의 최대 한도 안에서, 가장 높은 가격을 가지도록 물건을 채우자 (단, 하나의 물건을 나누어서 넣을 수는 없다)
이 알고리즘의 풀이 방법을 생각하기 전에, 우선 조금 특수한 형태의 Knapsack Problem으로 감을 잡아 보자.
(Fractional) Knapsack Problem (빈틈없이 배낭채우기 문제)
물건마다 특정한 무게와 가격을 가지고 있다고 하자. 또한 우리의 배낭은 물건을 채울 수 있는 최대 무게가 정해져 있다. 이때 목표는 다음과 같다.
배낭의 최대 한도 안에서, 가장 높은 가격을 가지도록 물건을 채우자 (단, 하나의 물건을 나누어서 넣을 수도 있다)
물건을 부분적으로 나누어 넣을 수 있다는 조건이 존재하는 경우, 이 문제를 greedy 알고리즘으로 해결할 수 있다는 사실이 알려져 있다. (이러한 조건이 없는 경우에는, Backtracking 혹은 Branch-and-Bound 알고리즘을 이용한다)
예를 들어 보자. 배낭이 30kg까지 담을 수 있다고 할 때,
item1 : 5kg / 50만원
item2 : 10kg / 60만원
item3 : 20kg / 140만원
이라고 가정하자. 배낭에 가장 높은 가격의 물건을 담기 위해서는 우선 단위 무게당 값어치가 높은 물건부터 최대한 넣고, 더 넣을 수 없는 경우 남은 무게만큼 잘라서 넣으면 된다.
따라서 단위 무게당 가치가 가장 높은 item1을 넣고, 다음으로 item3를 넣은 후, 남은 5kg에 물건을 넣기 위해 item2를 절반 잘라 넣으면 된다. 이렇게 시행하는 경우 총 220만원어치를 넣을 수 있게 된다.
일반적인 0-1 Knapsack Problem의 경우는?
물건을 나누어서 담을 수 없는 경우, greedy 알고리즘으로 문제를 해결할 수 없다. 이 경우에는 동적계획법에 해당하는 방법으로 문제를 해결하게 된다. 동적계획법에 기반하므로 기본적으로 재귀 구조를 사용하게 된다.
- 복습
Dynamic Programming (동적계획법) : 낮은 레벨의 문제부터 풀어 나가며 결과값을 저장하고, 이 결과들을 이용하여 높은 레벨의 문제에 대한 해답을 찾는 알고리즘 방식
우선 용어를 다음과 같이 정의하자
P[n][W] : n번째 물건까지를 이용하여, W 한도 내에서 채울 수 있는 최대 가격
이때 P[n][W]를 P[n-1][~]을 통해 계산한다고 생각해 보자. P[n-1][~]의 값은 이미 알고 있다고 가정한다. 이 값들을 기반으로 P[n][W]을 계산한다고 치면, 우리는 가장 처음으로 이러한 생각을 하게 되지 않을까?
n번째 물건을 포함하는 쪽이 맞을까, 아니면 포함하지 않는 쪽이 맞을까?
따라서 P[n][W]는, 아래의 두 가지 중 더 큰 쪽이 된다.
1. n번째 물건을 포함하지 않는 경우, 즉 n-1번째 물건까지만을 사용하여 W 한도로 배낭을 채우는 경우 : P[n-1][W]
2. n번째 물건을 포함하는 경우. 즉 n번째 물건을 무조건 포함하고, 나머지 n-1 번째 물건까지를 이용하여 남은 만큼의 무게를 채우는 경우를 의미한다. : n번째 물건의 가격 + P[n-1][W-wn] (wn은 n번째 물건의 무게를 의미한다).
위의 관계식을 이용하여 P[n][W]를 추측하면 되겠다.
적용해 보자!
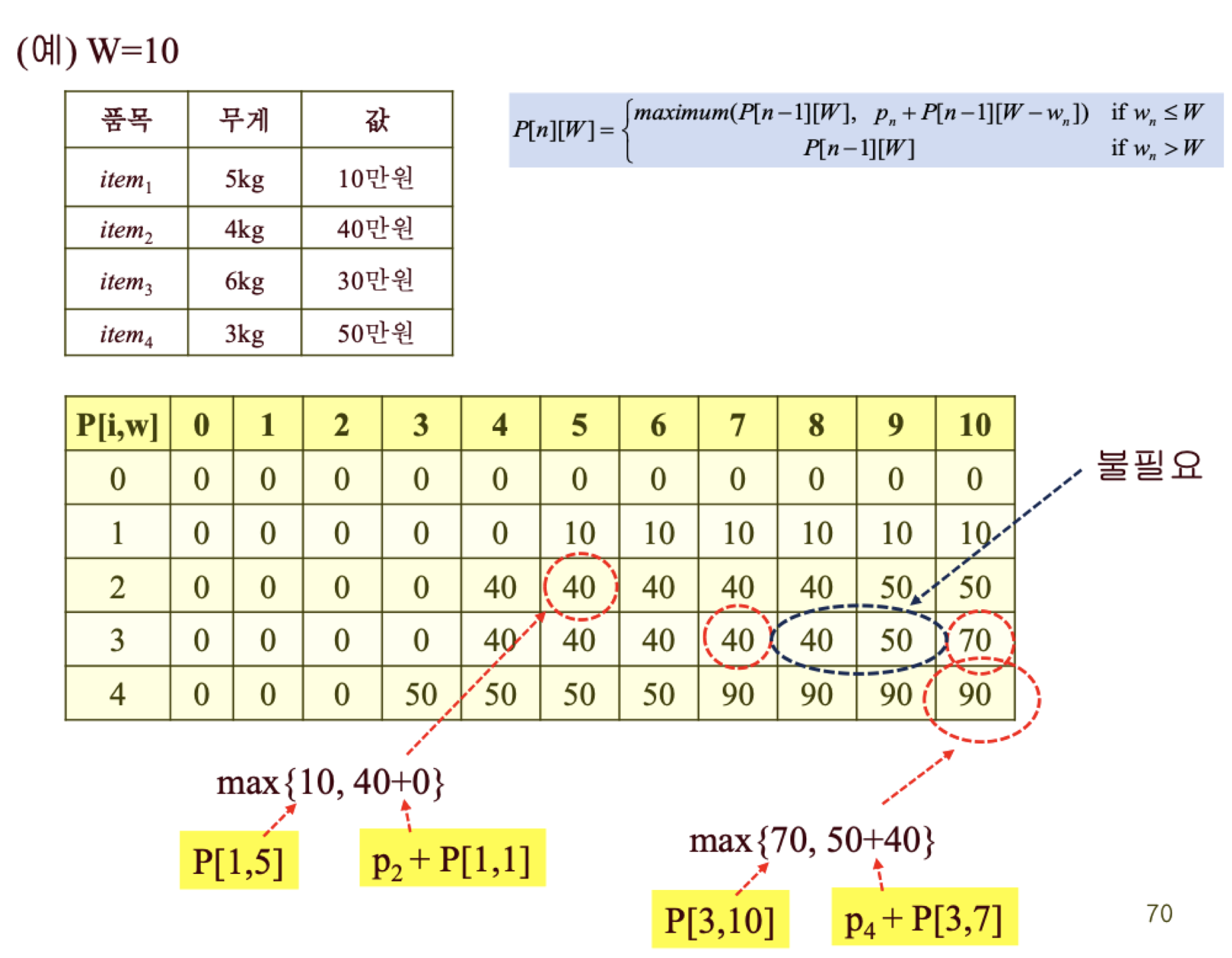
P[2][5]를 구하는 과정을 보자. P[2][5]는 P[1][5] (= 10)와, 40 + P[1][1]중 큰 값으로 결정된다. 이때 P[1][1]은 0임이 자명하므로 (한도가 1kg 이내인 물건은 없다), 2번 물건을 포함하는 쪽이 최적이 된다.
다음으로는 P[4][10]을 구하는 과정을 보자. 과정은 다음과 같다.
1. P[4][10] = Max(P[3][10], 50 + P[3][7]) = Max(70, 50 + 30) = 80
2. P[3][10] = Max(P[2][10], 30 + P[2][4]) = Max(50, 30 + 40) = 70
3. P[3][7] = Max(P[2][7], 30 + P[2][1]) = Max(40, 30 + 0) = 40
4. P[2][10] : item1, item2를 넣는 쪽이 최적임이 자명하므로, 10 + 40 = 50이다
5. P[2][4] : item2만 넣는 쪽이 최적임이 자명하므로, 40이다.
6. P[2][7] : item2만 넣는 쪽이 최적임이 자명하므로, 40이다.
7. P[2][1] : 아무것도 넣을 수 없으므로, 0이다.
- 위의 과정을 보면 알 수 있듯이, P 행렬 내의 특정 위치의 값을 구하기 위해, 해당 위치 왼쪽 및 위쪽의 모든 값을 구할 필요는 없다.
