트리란?
트리란 상위 원소에서 하위원소로 내려가면서 확장되는 나무모양의 자료구조이다. 트리는
1. 원소들끼리 상,하위 계층관계를 가지고 있는 계층형 자료구조이다.
2. 하나에 원소가 여러개에 원소로 뻗어나갈 수 있는 1:n의 관계를 가진다.
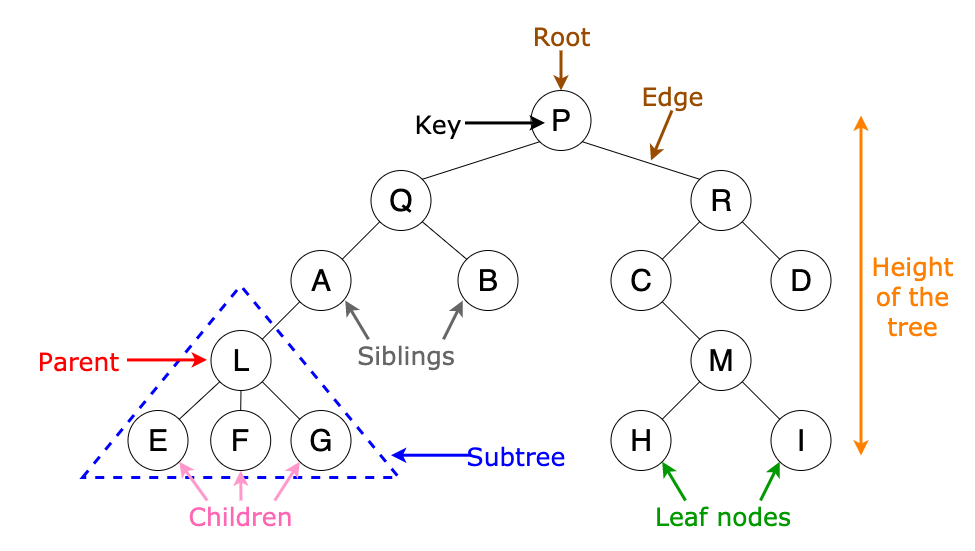
트리의 특징
트리는 DAG(Directed Acyclic Graph)의 한 종류로, 그래프와 많이 비교된다. 그래프와 트리의 차이를 자세히 알고 싶은 사람은 아래 참고란에 있는 *트리 vs 그래프 링크를 보면 많은 도움이 될 것이다. 여기서는 그냥 트리의 특징만 알고 넘어간다.
- 반드시 하나의 시작 노드인 root노드를 가진다.(= 들어오는 간선 없음)
- (루트를 제외한)임의의 노드로 갈 수 있는 경로는 1개만 존재한다. (= 루트를 제외한 모든 노드들은 반드시 들어오는 간선 딱 1개만 가진다.)
- DAG(Directed Acyclic Graph)의 한 종류로 싸이클이 없고 방향성(부모 -> 자식)을 가지는 그래프이다.
- N개의 노드가 존재한다면 간선의 수는 항상 N-1이다.
트리 용어
root node
트리의 시작노드
node
트리의 원소
형제노드
: 같은 부모 노드의 자식들 (부모가 같고, 같은 높이에 있음)
조상노드
: 루트 노드까지 이어지는 간선 경로에 있는 모든 상위 노드들
자손노드
: 서브트리에 있는 하위 노드들
단말 노드
: 차수가 0인 노드. 즉, 자식 노드가 없는 노드
edge(간선)
노드(트리의 원소)를 연결하는 선. 즉, 상위(부모)노드와 하위(자식)노드를 연결
degree(차수)
노드의 차수 : 연결된 자식 노드의 수
트리의 차수 : 전체 노드 중 차수가 가장 큰 노드의 차수
height/level(높이/레벨)
루트노드에서 특정 노드까지 가는데 필요한 간선의 수
트리의 높이 : 가장 먼 노드의 레벨
트리의 종류
이진트리
이진트리는 각 노드가 최대 2개의 자식 노드(왼쪽 자식, 오른쪽 자식)를 가질 수 있는 트리를 말한다.
이진 트리는 배열로 구현할 수 있지만, 수정과 삽입을 용이하게 하기 위해 Linked List를 쓰기도 한다.
- 포화(full) 이진트리
: 모든 레벨에 노드가 포화상태로 차 있는 이진트리. 즉 높이가 n 일 때 1 + 2 + 4 + ... + 2^n = 2^(n+1) - 1 개의 노드를 가지는 이진트리
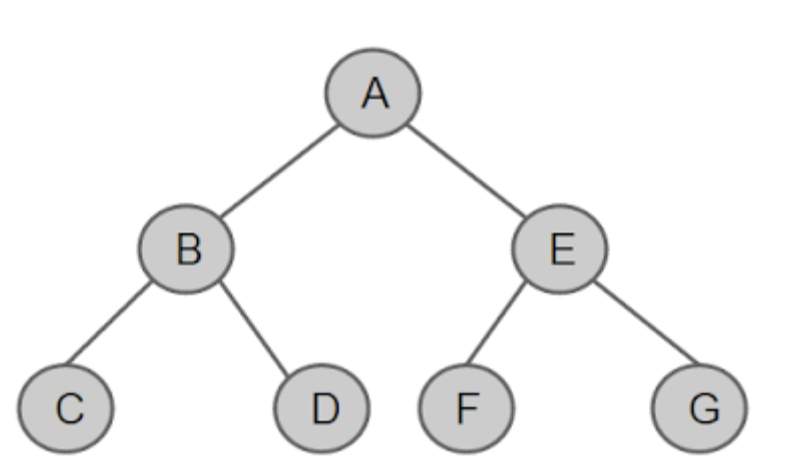
- 완전(Complete) 이진트리
: 부모 -> 왼쪽 -> 오른쪽 순서로 트리를 채워 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드들이 왼쪽에 있는 이진트리
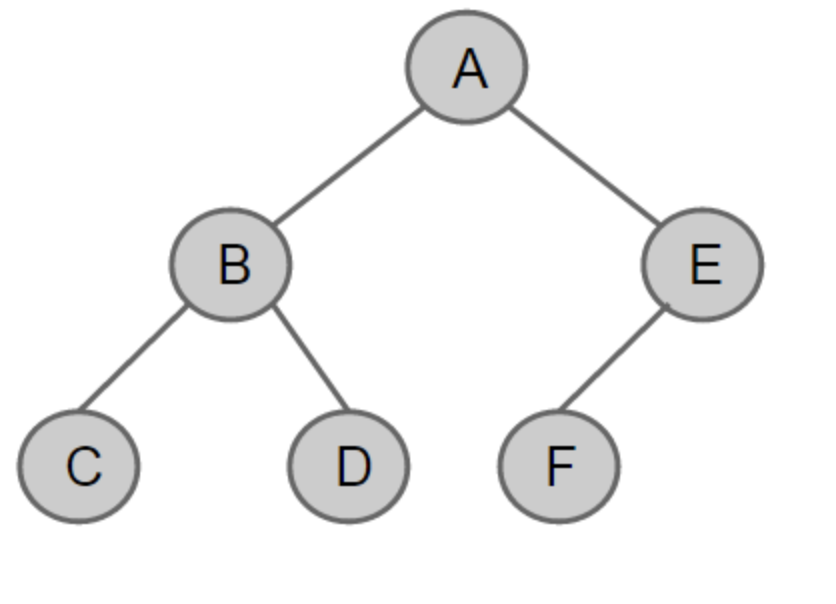
- 이진 탐색 트리(BST)
: 모든 원소가 유일한 값을 가지고 있으며, 루트 노드를 기준으로 왼쪽 서브트리의 키 값은 루트 노드의 키 값보다 작고, 오른쪽 서브트리의 키 값은 루트 노드의 키 값보다 큰 값을 가진다. 그리고 서브트리들도 이진 탐색 트리이다.
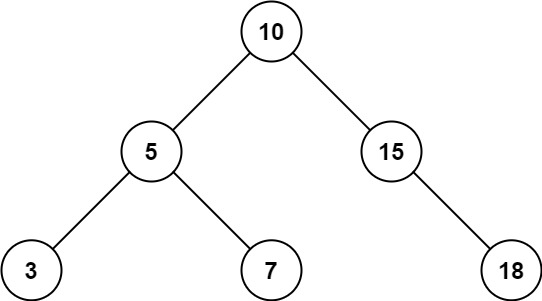
- 힙(Heap)
: 키 값이 가장 큰/작은 노드를 찾기 위한 완전 이진트리. 키 값을 이용하여 우선순위 큐(PriorityQueue)를 구현
- max heap
항상 root 노드의 키 값이 가장 큼
부모 노드의 키값은 반드시 자식노드의 키 값보다 크도록 유지한다.
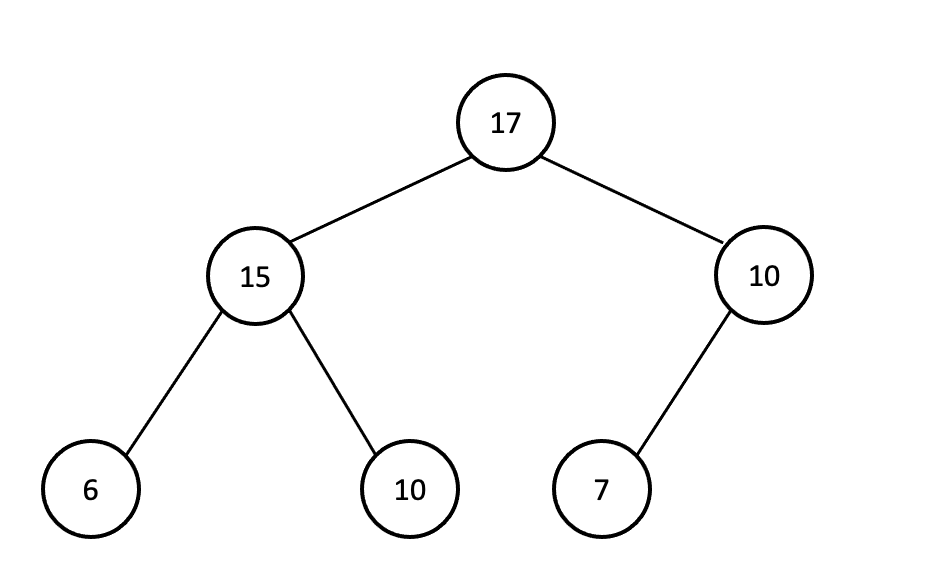
- min heap
항상 root 노드의 키 값이 가장 작음
부모 노드의 키값은 반드시 자식노드의 키 값보다 작게 유지한다.
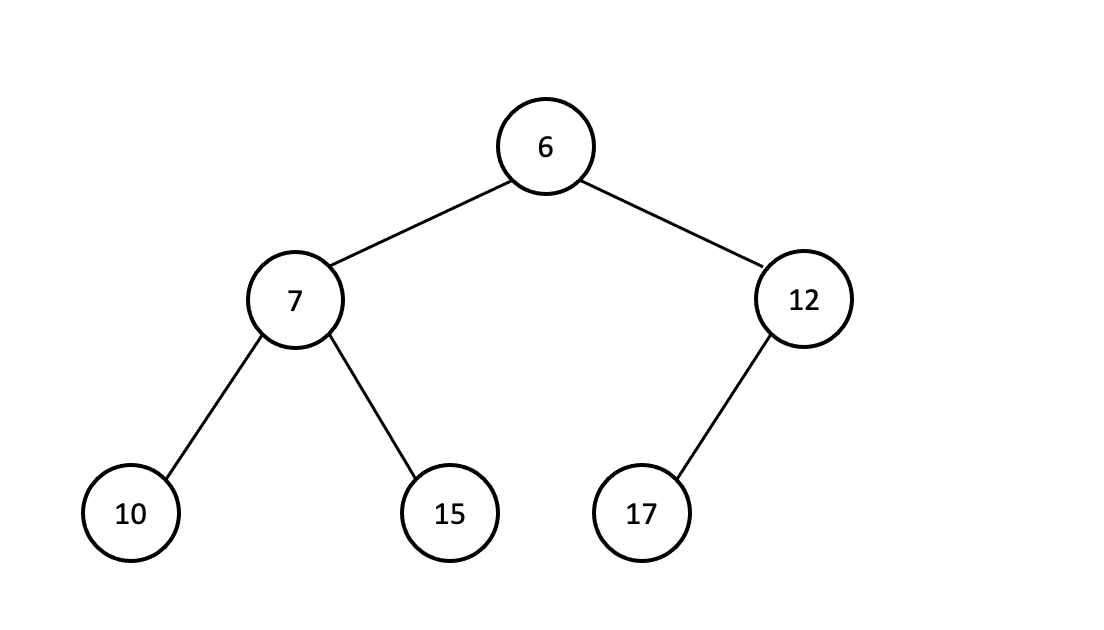
참고
트리 vs 그래프 :
http://freefeast.info/difference-between/difference-between-trees-and-graphs-trees-vs-graphs/


트리 이미지가 인상깊네요