[Python] 시그모이드(Sigmoid) 함수와 로지스틱 회귀(Logistic Regression)

로지스틱 회귀 모델은 시그모이드(sigmoid) 함수를 사용하여 데이터를 설명한다. 이름에 회귀가 들어있지만 사실 로지스틱 회귀는 분류(classification)에 사용된다.

로지스틱 회귀란?

• 사건(Event)이 발생할 가능성을 예측하는 데 사용하는 모델

그렇다면, 시그모이드 함수는 무엇일까? 시그모이드 함수에 대해 먼저 알아보도록 하자.

1. 시그모이드 함수란?

시그모이드 함수는 로지스틱 회귀에서 활성화(Activation) 함수로 사용된다. 식은 다음과 같다.

$S(x)=$ $1\over{1+e^{-x}}$ $=$ $e^x\over{e^x +1}$

시그모이드 함수는 입력값을 0과 1사이의 값으로 출력하는데, y축 값 0.5를 기준으로 'Yes' or 'No'를 구분하여 이진/다중 분류에 강한 모델을 만든다. 시그모이드 함수를 코드로 구현해보자.

import numpy as np
import matplotlib.pyplot as plt

# Sigmoid func
def sigmoid(x):
    return 1 / (1+np.exp(-x)) # np.exp는 밑이 e인 지수함수로 변환

# 함수 테스트용 데이터 생성
test = np.array([-1,0,1])

print(sigmoid(test))

result: [0.26894142 0.5 0.73105858]

시그모이드 함수를 만들었으니 출력해보자.

# sigmoid graph
sigmoid_x = range(-6,7)
sigmoid_y = sigmoid(np.array(sigmoid_x))

plt.plot(sigmoid_x, sigmoid_y, color='blue', linewidth = 0.5)

# 백그라운드 격자 생성
plt.rcParams['axes.grid'] = False

# 선 굵기 설정
plt.axvline(x=0, color='black', linewidth=3)

plt.yticks([0,0.5,1])
plt.show()

# -6~6의 입력값들을 0과 1 사이의 값으로 변환해주는 로지스틱 함수 생성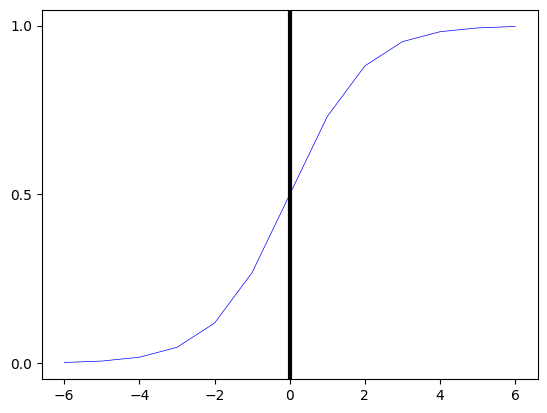

시그모이드 함수는 0과 1사이의 값으로 이루어져있고 S자 형태의 그래프다. 즉, 입력값들이 연속적인 값으로 출력된다는 의미이다. 그래프를 보면 알 수 있듯이, X가 0보다 크면, Y는 0.5보다 큰 값(사건이 발생)을 나타낸다. 반대로 0보다 작은 경우 y는 0.5보다 작은 것(사건이 발생하지 않음)을 나타낸다.

선형 함수의 경우 이상치 같은 새로운 데이터가 생겼을 때, 모델에 악영향을 끼치는 경우가 있다. 하지만, 시그모이드 함수는 0과 1사이의 곡선 형태의 그래프이기 때문에 이상치의 영향을 크게 받지 않는다는 장점이 있다.

이제 로지스틱 회귀에 대해 알아보도록 하자.

2. 로지스틱 회귀

직접 코드를 구현해보면서 로지스틱 회귀가 분류에 적합한 모델인 지 확인해보도록 하자. 우선, 데이터를 구성해보자. x값은 3부터 17까지 구성되어 있고 x값이 9에서 10으로 넘어갈 때, y값도 0에서 1로 넘어가도록 준비한다.

# 학습 데이터 생성
x_train = [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
y_train = [0,0,0,0,0,0,0,1,1,1,1,1,1,1,1]

x_test = [0,1,2,18,19]
y_test = [0,0,0,1,1]

x_train = np.array(x_train).reshape(-1,1)
y_train = np.array(y_train)

x_test = np.array(x_test).reshape(-1,1)
y_test = np.array(y_test)

print(x_train)
print(y_train)

from sklearn.linear_model import LogisticRegression

# 로지스틱 회귀 생성
logi_reg = LogisticRegression()

# 학습
logi_reg.fit(x_train, y_train)

print('intercept : ', logi_reg.intercept_)
print('coef : ', logi_reg.coef_)

intercept : [-11.34126808]
coef : [[1.19383367]]

# intercept 와 coef를 수동으로 만들기
odd = []
for i in x_train:
    odd.append((logi_reg.coef_+i) + logi_reg.intercept_)

sigmoid_y = sigmoid(np.array(odd)).reshape(-1,1)

# 역산된 그래프 표시
plt.scatter(x_train, y_train, color='red')
plt.plot(np.array(x_train), sigmoid_y, color='blue')
plt.rcParams['axes.grid']= True
plt.yticks([0,0.5,1])
plt.ylim([-0.1,1.1]) # y축의 범위
plt.show()

coef와 intercept를 이용하여 그린 sigmoid 그래프가 데이터를 잘 표현하고 있다. 이처럼 로지스틱 회귀는 범주형 데이터를 예측하는 이진분류에 적합하다는 것을 확인할 수 있다.