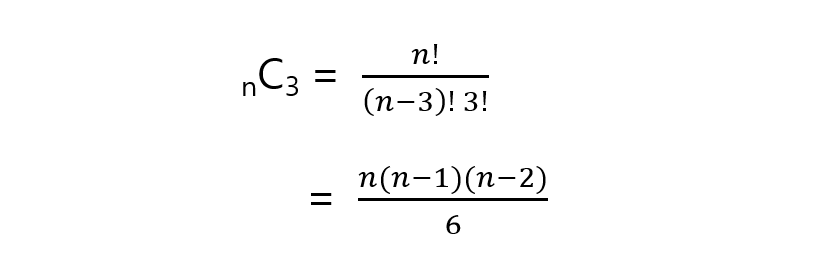[백준] 24267번 - 알고리즘 수행 시간 (Java)

문제

문제 링크

풀이

방법 1

3차항의 시간복잡도인 것은 명백하니 일단 n(n-1)(n-2)로 잡고, 예제 출력에 맞추어 6을 나누었다는 풀이도 있었다.

빠른 시간 내에 풀기 위해서는 나쁘지 않은 방법인 것도 같다.

방법2

고등수학에서의 조합을 이용하는 풀이를 발견했다. 참고 블로그

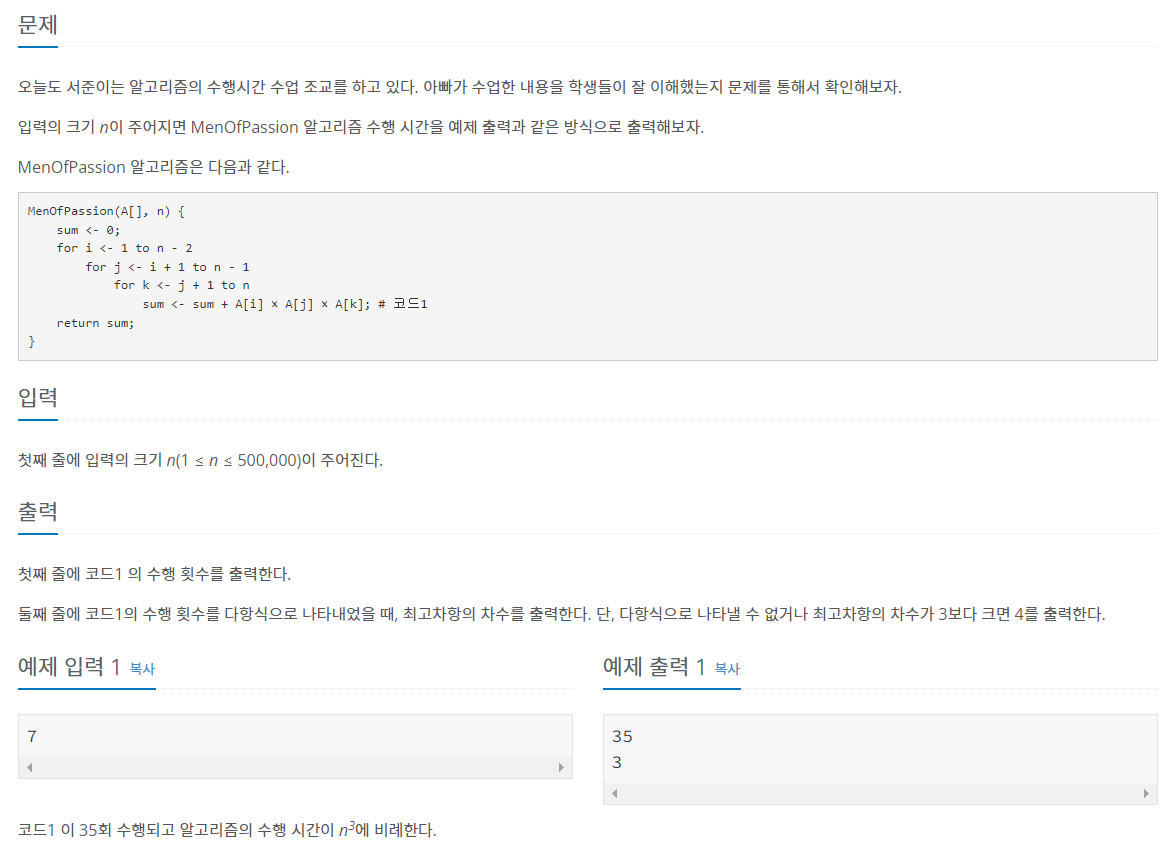
이번 문제는 i, j, k에 따라 세번 반복문이 중첩된 경우이다.

i는 1부터 (n-2)까지 반복
j는 i+1부터 (n-1)까지 반복
k도 j+1부터 (n)까지 반복

즉, n=7이고 i=1, j= 2이면
k는 3, 4, 5, 6, 7이 가능하다.
=> 즉, (i,j,k)는 (1,2,3), (1,2,4), ...., (1,2,7)이 가능한 것!!

j는 i+1부터, k는 j+1부터 시작하므로 세 숫자가 중복될 수는 없다!

따라서 1부터 n=7까지의 숫자 중 중복 없이 i,j,k를 선택하는 경우인 것!
이는 조합의 공식을 활용하면 된다.

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader( new InputStreamReader(System.in));
        Long n = Long.parseLong(br.readLine()); // int는 불가


        System.out.println( n*(n-1)*(n-2)/6);   // n개의 수 중 i,j,k 3개를 중복없이 고르는 조합
        System.out.println(3);    // O(n^3)의 시간복잡도이므로 최고차항은 3차
    }
}