Python3,DP
문제

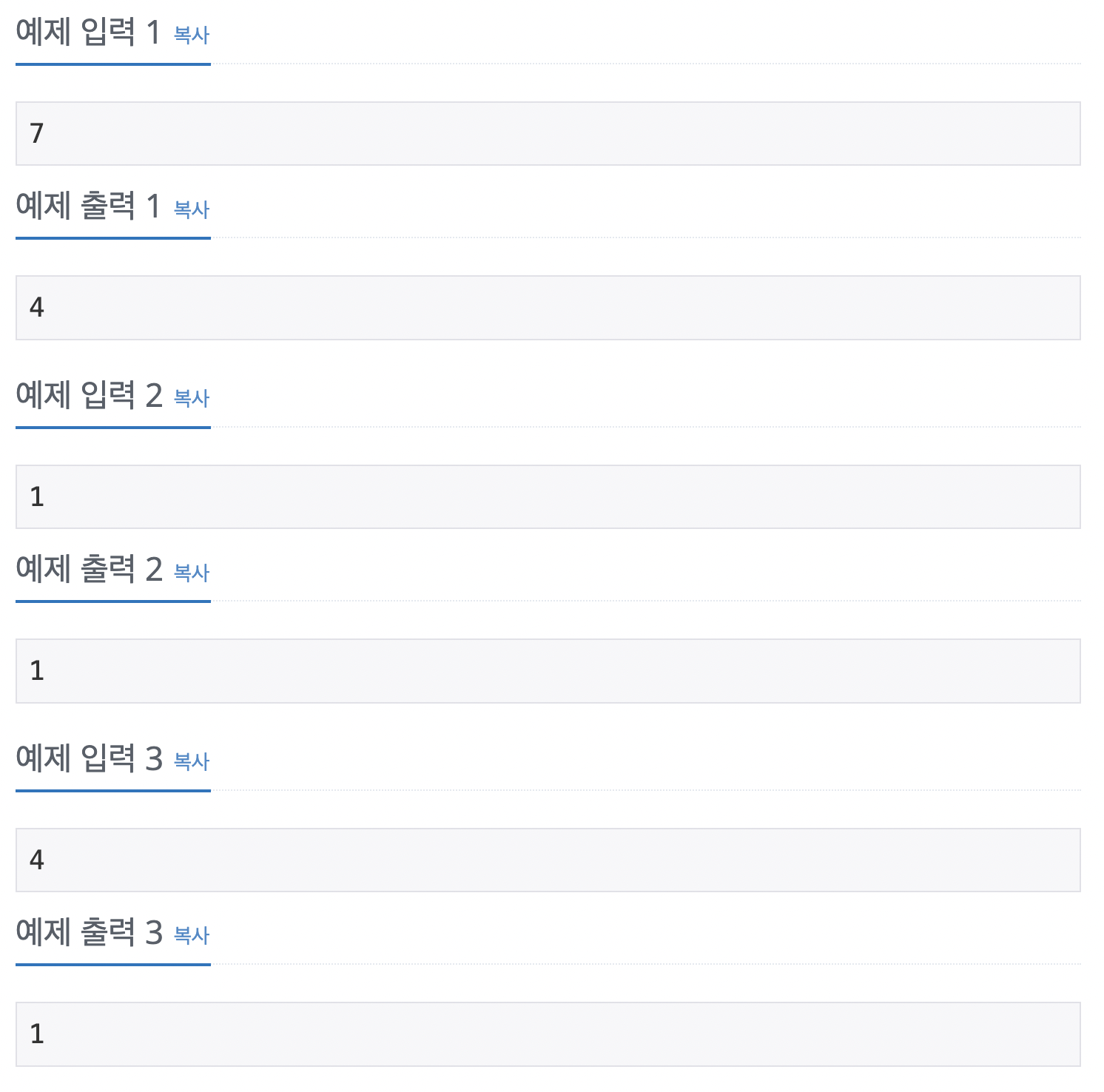
입출력
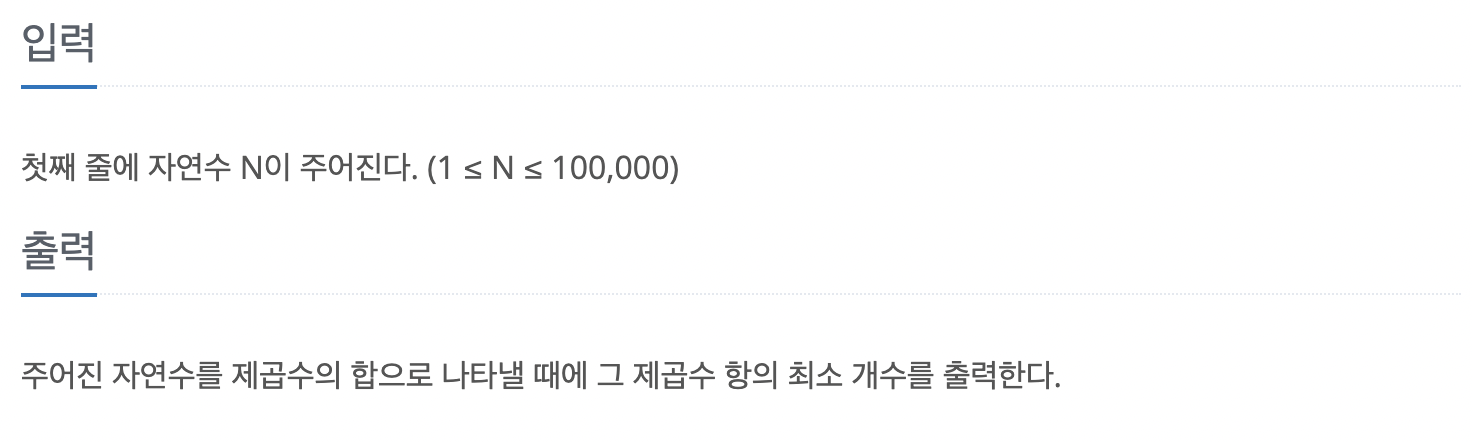
입출력 예시
주요 포인트
이중 반복문이 필요하다.
i는 1부터 n까지, j는 1부터 i-1까지 순회한다.
만약 j의 제곱이 i보다 크면 제곱수가 주어진 수보다 큰 것이기 때문에 반복을 중단한다.
만약 dp[i]가 dp[i-jxj] + 1 보다 크면
dp[i]에 dp[i-jxj] + 1 값을 넣어준다.
1을 더하는 이유는 가장 작은 값이 0이고 1을 더해야 해당 최소항의 값이 나오기 때문이다.
ex) dp[4]는 1이다. 식에 대입하면 dp[4-2*2] = 0이 나오는데 이때 1을 더해야 dp[4]의 값이 나온다.
dp 0 1 2 3 4 5 6 7 일 때,
i가 4이고, j가 2이면 dp[4] = 4이었다가
dp[4-2x2] + 1 = dp[0] + 1 = 1 로 dp[4]는 1이 된다.
i가 5이고, j가 2이면 dp[5] = 5이었다가
dp[5-2x2] + 1 = dp[1] + 1 = 1 로 dp[5]는 2가 된다.
i가 6이고, j가 3이면 dp[6] = 6이었다가
dp[6-2x2] + 1 = dp[2] + 1 = 1 로 dp[6]는 3이 된다.
i가 7이고, j가 2이면 dp[7] = 7이었다가
dp[7-2x2] + 1 = dp[3] + 1 = 1 로 dp[7]는 4가 된다.
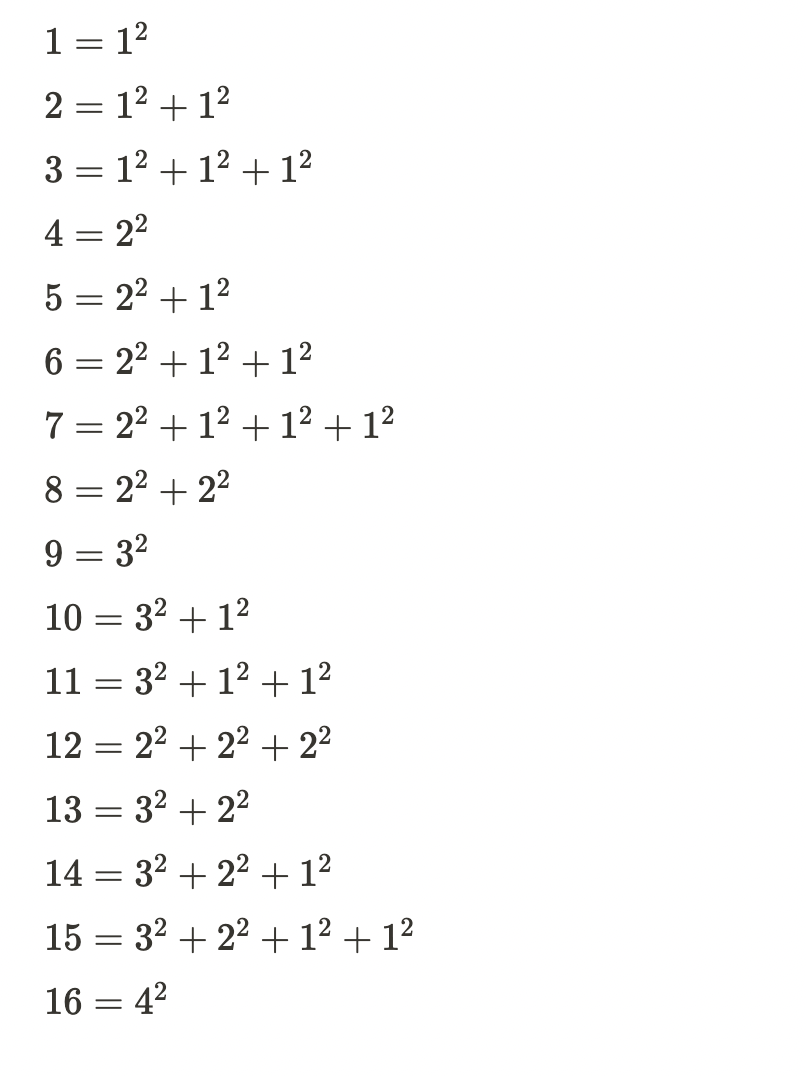
DP 문제는 규칙을 찾을 때까지 나열해 봐야 한다.
최종 코드
n = int(input())
dp = [i for i in range(n+1)]
for i in range(1, n+1):
for j in range(1, i):
if j*j > i:
break
if dp[i] > dp[i-j*j] + 1:
dp[i] = dp[i-j*j] + 1
print(dp[n])
피드백
혼자 규칙을 찾기 어려운 문제였다. 다양한 유형의 문제를 풀면서 문제 푸는 방법을 익혀야 겠다.
