[BOJ] 2609. 최대공약수와 최소공배수

Python3

문제

입출력

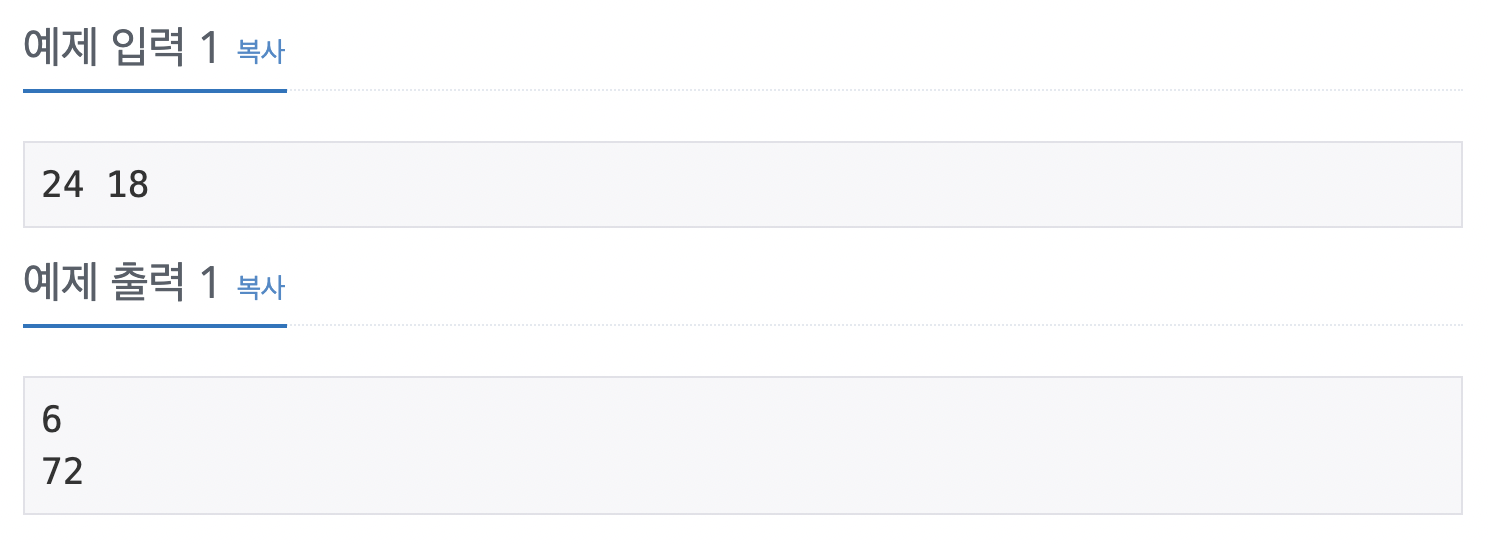
입출력 예시

주요 포인트

유클리드 호제법
a & b의 최대 공약수는 b & a를 b로 나눈 나머지의 최대 공약수와 같다.
단, a > b여야 a를 b로 나눈 나머지를 구할 수 있다.

a, b
= b, a % b = b, r
= r, b % r = r, r'
= r', r % r' = r',r''

이 과정을 반복하여 나머지(r'')가 0이 되었을 때 나누는 수(r')가 a와 b의 최대공약수이다.
나누는 수(r')은 a로 저장되어 있으므로 a를 return한다.

최소공배수는 a와 b의 곱을 a와 b의 최대 공약수로 나눈 값

최종 코드

a, b = map(int, input().split())

def gcd(a, b):
    while b > 0:
        a, b = b, a % b
    return a
    
def lcd(a, b):
    return a * b // gcd(a, b)

print(gcd(a, b))
print(lcd(a, b))

피드백

최대공약수와 최소공배수는 유클리드 호제법에 대해서 알고 있어야 한다.
최대공약수는 b가 0이 되기 전까지 a, b에 b, a%b 값을 넣는다. 이후 a(나누는 수)를 리턴한다.
최소공배수는 a와 b를 곱한 값을 a와 b의 최대공약수로 나눈 몫이다.

참고

https://rladuddms.tistory.com/107