알고리즘에서 문자열 패턴을 찾을 수 있다.
문자열 패턴 매칭 문제의 정의는 아래와 같다.

이 때, 문자열 X 안에 문자열 Y가 존재하는가?
이를 완전 탐색으로 풀면 아래와 같이 풀 수 있다.
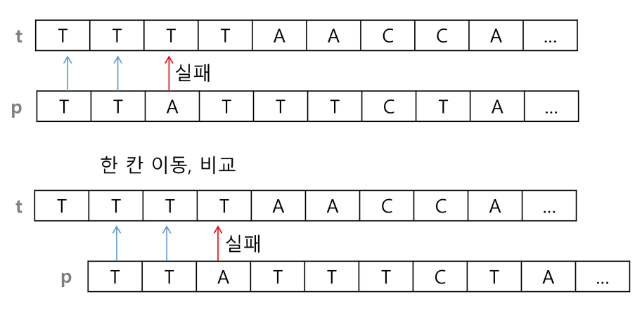
해당 알고리즘의 시간 복잡도는 O(MN) 이다. 좀 더 효율적인 방법을 찾아보자.
문자열 패턴 매칭 문제에 라빈-카프 알고리즘을 활용할 수 있다.
문자열 검색을 위해 해시 값 함수를 사용하는 알고리즘을 라빈-카프 알고리즘이라 한다.
원리는 아래와 같다.

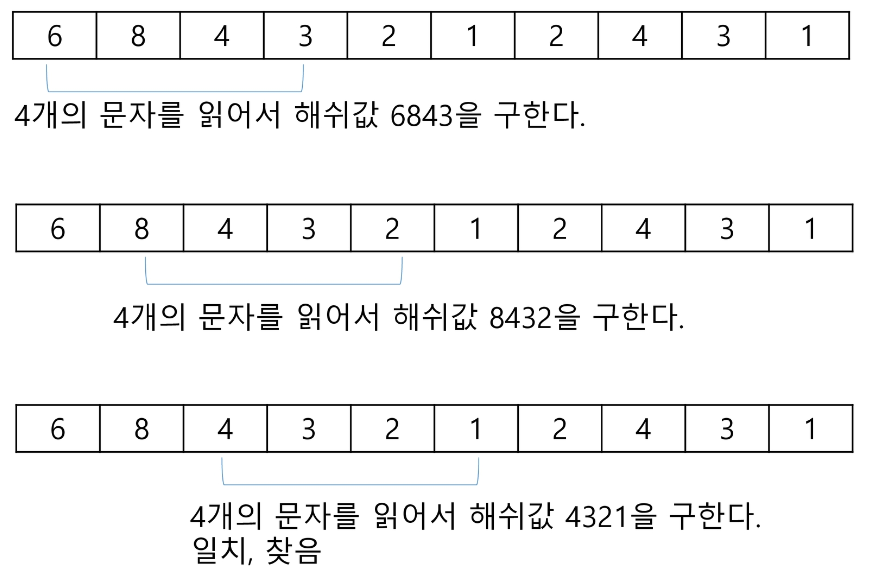
찾으려는 패턴의 해시 값은 패턴을 숫자로 바꾼 4321이라 가정해보자.
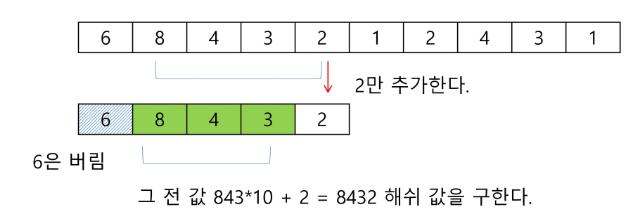
그럼 숫자 문자열을 패턴의 길이만큼 잘라 해시 값을 구해 해시 값이 같으면 패턴이 있다고 판단한다.
이 때 아래처럼 슬라이딩 윈도우를 활용할 수 있다.
해당 알고리즘의 고려사항은 아래와 같다.
- 패턴이 문자열이며 길이가 길어지면 길이에 제한을 두기 위해 mod 연산을 취한다.
- 1번 연산으로 인해 해시 값이 일치하는 해시 충돌이 일어날 수 있고, 이 때는 문자열이 일치하는 지 하나하나씩 다시 검사한다.
해당 알고리즘의 시간 복잡도는 최악의 경우 O(MN) 이지만, 대부분 O(1)에 가깝다.
문자열 패턴 매칭 문제에 보이어 무어 알고리즘을 활용할 수 있다.
문자열을 오른쪽에서 왼쪽으로 비교하는 알고리즘을 보이어 무어 알고리즘이라 한다.
원리는 아래와 같다.
문자열의 오른쪽 끝에 있는 문자가 불일치하고 이 문자가 패턴 내에 존재하지 않을 때를 살펴보자.
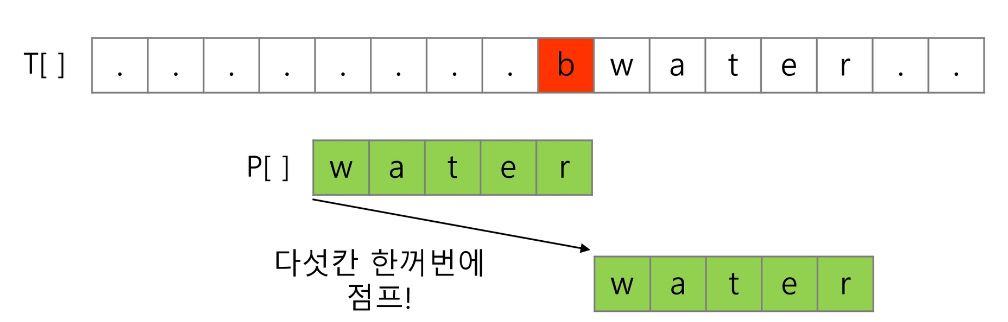
비교 문자열 크기만큼 점프가 가능하다.
이번엔 문자열의 오른쪽 끝에 있는 문자가 불일치하고 이 문제가 패턴 내에 존재할 때를 살펴보자.
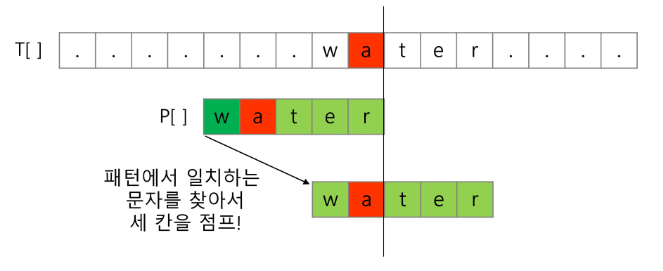
일치하는 문자가 있는 곳까지 점프가 가능하다.
따라서 패턴 불일치가 발생할 때 본문 포인터의 점프 횟수를 기록한 skip 배열을 만든다.
아래는 rithm 패턴 문자열의 skip 배열 예시다.

skip 배열을 이용하면 아래와 같이 비교된다.
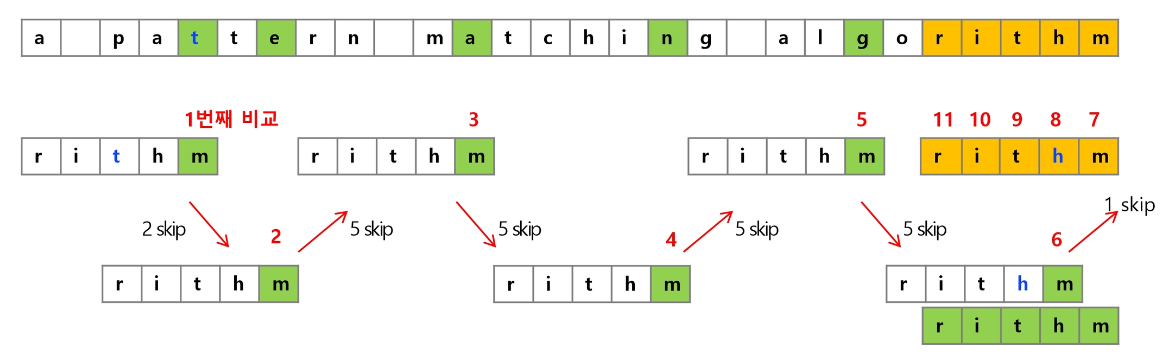
해당 알고리즘의 시간 복잡도는 최악의 경우 O(MN) 이지만, 최선의 경우 O(N/M) 이다.
평균적으로 가장 빠른 속도를 가지는 알고리즘이기도 하다.
