Algorithm 4일차

알고리즘에서 부분집합을 활용할 수 있다.

부분집합이란 집합에 포함된 원소들을 선택하는 것을 의미한다.
집합의 원소가 n개일 때, 공집합을 포함한 부분집합의 수는 2^n개 이다.

부분집합을 재귀로 구현하면 아래와 같다.

import java.util.Scanner;

public class SubSet {
	static int N, totalCnt;
	static int[] input;
	static boolean[] isSelected;
	
	static void generateSubset(int cnt) {
		if (cnt == N) {
			totalCnt++;
			
			for (int i = 0; i < N; i++) {
				if (isSelected[i] == true) {
					System.out.print(input[i] + " ");
				}
			}
			System.out.println();
			
			return;
		}
		
		// 현재 원소를 부분집합의 구성에 포함
		isSelected[cnt] = true;
		generateSubset(cnt + 1);
		
		// 현재 원소를 부분집합의 구성에 미포함
		isSelected[cnt] = false;
		generateSubset(cnt + 1);
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		input = new int[N];
		isSelected = new boolean[N];
		
		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();
		}
		
		generateSubset(0);
		System.out.println("총 갯수 : " + totalCnt);
		
		sc.close();
	}
}

부분집합의 대표적인 예시는 원소의 조합이 특정 값인 원소의 조합을 찾는 문제이다.
아래 문제를 살펴보자.

유한 개의 정수로 이루어진 집합이 있을 때,
이 집합의 부분집합 중 그 집합의 원소를 모두 더한 값이 0이 되는 경우를 찾아라.

해당 문제는 아래처럼 풀 수 있다.

import java.util.Scanner;

public class SubSetSum {
	static int N;
	static int[] input;
	static boolean[] isSelected;
	
	static void generateSubset(int cnt, int sum) { // cnt : 직전까지 고려된 원소 수, sum : 직전까지 선택된 원소들의 합
		if (cnt == N) {
			if (sum == 0) {
				int falseCount = 0;
				
				for (int i = 0; i < N; i++) {
					if (isSelected[i] == false) {
						falseCount++;
					}
				}
				
				if (falseCount == N) {
					return;
				}
				
				for (int i = 0; i < N; i++) {
					if (isSelected[i] == true) {
						System.out.print(input[i] + " ");
					}
				}
				System.out.println(": " + sum);
			}
			
			return;
		}
		
		// 현재 원소를 부분집합의 구성에 포함
		isSelected[cnt] = true;
		generateSubset(cnt + 1, sum + input[cnt]);
		
		// 현재 원소를 부분집합의 구성에 미포함
		isSelected[cnt] = false;
		generateSubset(cnt + 1, sum);
	}
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		input = new int[N];
		isSelected = new boolean[N];
		
		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();
		}
		
		generateSubset(0, 0);
		
		sc.close();
	}
}

빈 배열은 제외했다.

※ 순조부의 계산량을 살펴보자.
순열은 12!에서 약 5억, 조합은 30C15에서 약 1억 5천만, 부분집합은 2^30에서 약 10억이다.

알고리즘에서 비트 연산을 활용할 수 있다.

아래와 같은 연산을 비트 연산이라고 한다.

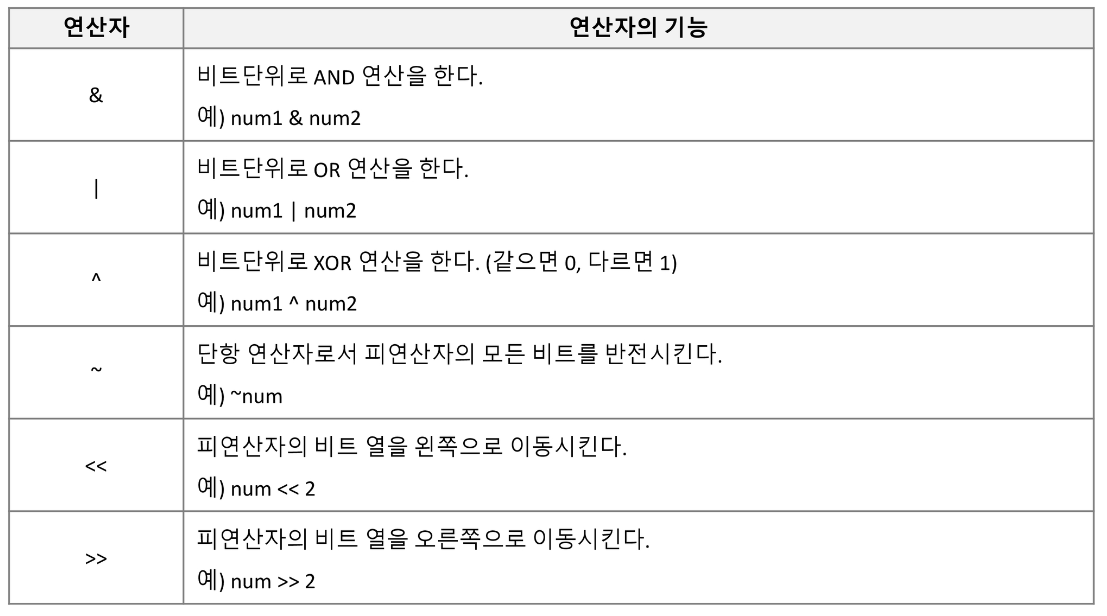
주로 쓰이는 비트 연산은 아래와 같다.
(number & 1 << n != 0) : n+1 자리의 비트가 1인지 확인
(number | 1 << n != number) : n+1 자리의 비트를 1로 만들고, 제대로 반영됐는지 확인

비트 연산으로 부분집합을 표시할 수 있다. 아래 코드를 살펴보자.

public class BinaryCounting {

	public static void main(String[] args) {
		int arr[] = {3, 6, 7, 1, 5, 4};
		int n = arr.length;
		
		for (int i = 0; i < (1 << n); i++) { // 부분집합의 갯수
			for (int j = 0; j < n; j++) {
				if ((i & 1<<j) != 0) {
					System.out.print(arr[j] + " ");
				}
			}
			System.out.println();
		}
	}
}

공집합을 포함한 64개의 부분집합이 출력된다.

※ boolean 연산 대신 비트 연산을 사용한다고 시간복잡도가 낮아짐을 보장하진 않는다.