Algorithm 8일차

알고리즘에서 트리를 탐색할 때 BFS를 활용할 수 있다.

BFS를 사용하면 레벨을 기준으로 트리를 탐색할 수 있다. 아래 사진을 살펴보자.

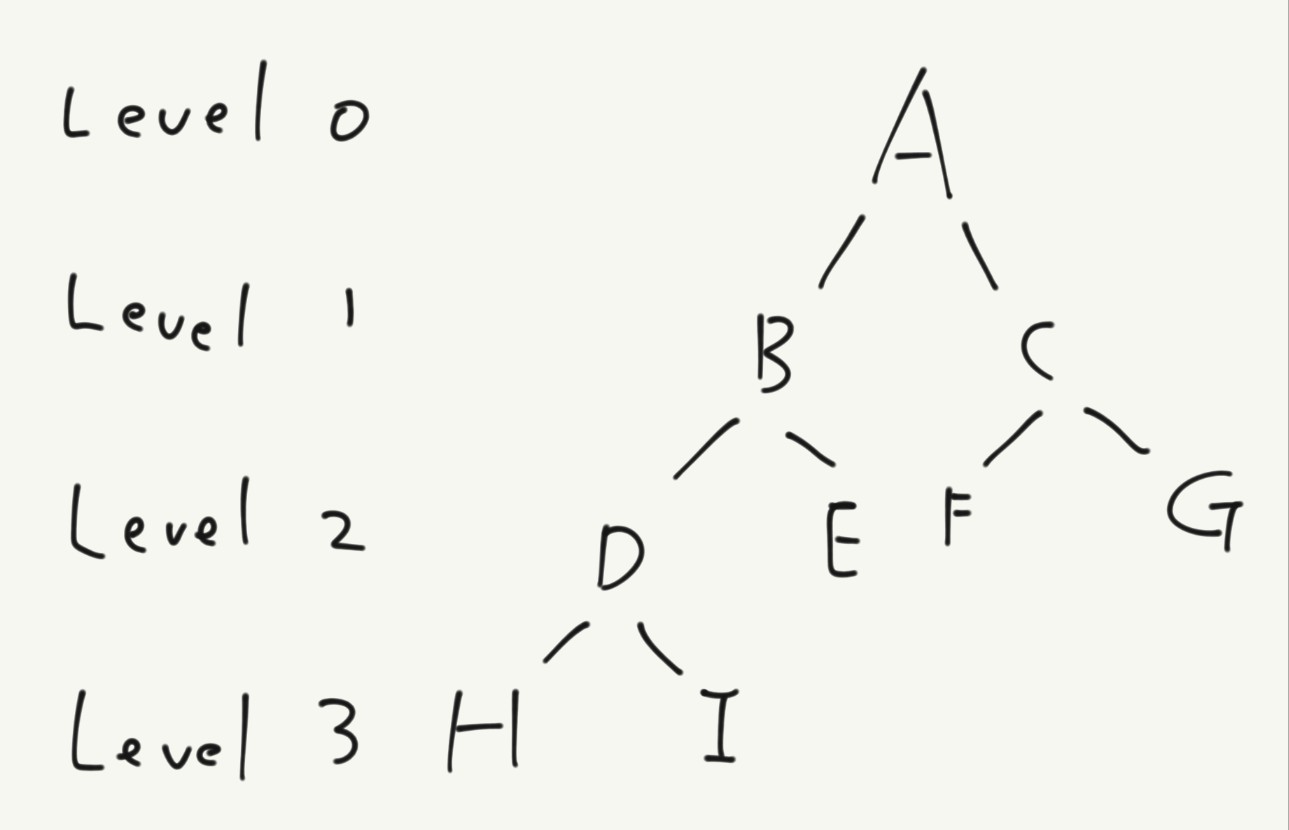
BFS를 사용하면 Level 0 -> 1 -> 2 -> 3 순으로 트리를 탐색할 수 있다.
이를 구현한 코드는 아래와 같다. BFS는 큐를 사용한다.

import java.util.ArrayDeque;
import java.util.Queue;

class CompleteBinaryTree<T> {
	private static int SIZE;
	private static Object[] nodes;
	private int lastIndex;
	
	public CompleteBinaryTree (int size) {
		SIZE = size;
		nodes = new Object[size+1];
	}
	
	private boolean isFull() {
		return lastIndex == SIZE;
	}
	
	public void add(T e) {
		if (isFull()) {
			return;
		}
		nodes[++lastIndex] = e;
	}
	
	public void bfs() {
		Queue<Integer> queue = new ArrayDeque<>();
		queue.offer(1);
		
		int current = 0;
		int size;
		int level = 0;
		
		while (!queue.isEmpty()) {
			size = queue.size();
			System.out.print("level " + level + " : ");
			
			while (--size >= 0) {
				current = queue.poll();
				System.out.print(nodes[current] + " ");
				
				if (current * 2 <= lastIndex) {
					queue.offer(current * 2);
				}
				
				if ((current * 2 + 1) <= lastIndex) {
					queue.offer((current * 2 + 1));
				}
			}
			level++;
			System.out.println();
		}
	}
}

public class CompleteBinaryTreeTest {

	public static void main(String[] args) {
		int size = 9;
		
		CompleteBinaryTree<Character> tree = new CompleteBinaryTree<> (size);
		
		for (int i = 0; i < size; ++i) {
			tree.add((char)(65 + i));
		}
		
		tree.bfs();
	}
}

실행 결과는 아래와 같다.

level 0 : A
level 1 : B C
level 2 : D E F G
level 3 : H I

알고리즘에서 트리를 탐색할 때 DFS를 활용할 수 있다.

트리의 노드들을 체계적으로 방문하는 것을 순회라고 한다.
순회에는 아래 3가지 방법이 있다.

1. 전위 순회 : 자신 -> 왼쪽 자식 -> 오른쪽 자식 순으로 방문한다.
2. 중위 순회 : 왼쪽 자식 -> 자신 -> 오른쪽 자식 순으로 방문한다.
3. 후위 순회 : 왼쪽 자식 -> 오른쪽 자식 -> 자신 순으로 방문한다.

실제로 트리를 순회해보자. 아래 트리를 3개의 순회 방법으로 순회해보자.

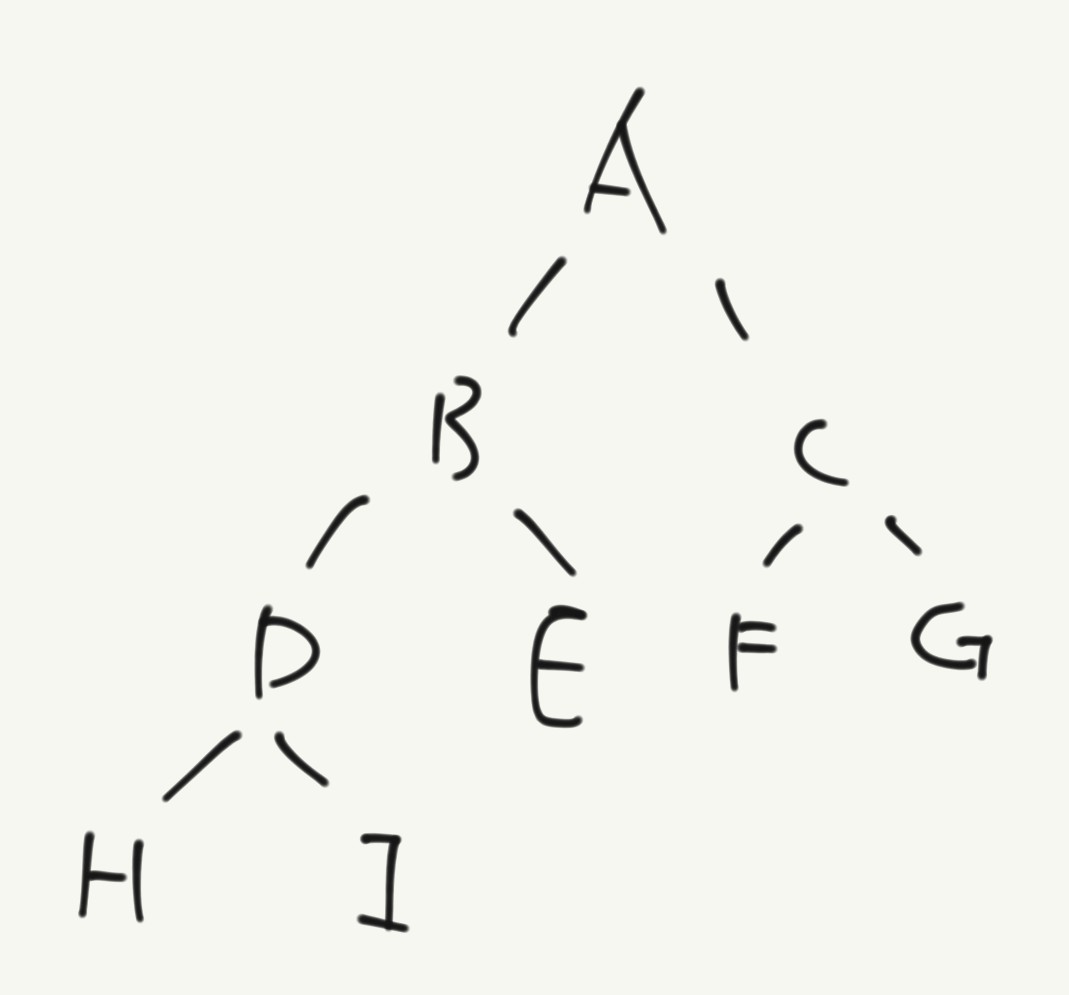
먼저 전위 순회이다. 전위 순회를 구현한 코드는 아래와 같다.

...
public void dfsByPreOrder() {
	System.out.print("PreOrder : ");
	dfsByPreOrder(1);
	System.out.println();
}

private void dfsByPreOrder(int current) {
	System.out.print(nodes[current] + " ");

	if (current*2 <= lastIndex) {
		dfsByPreOrder(current * 2);
	}

	if ((current*2 + 1) <= lastIndex) {
		dfsByPreOrder(current * 2 + 1);
	}
}
...

실행 결과는 아래와 같다.

A B D H I E C F G

다음으로 중위 순회이다. 중위 순회를 구현한 코드는 아래와 같다.

...
public void dfsByInOrder() {
	System.out.print("InOrder : ");
	dfsByInOrder(1);
	System.out.println();
}

private void dfsByInOrder(int current) {
	if (current*2 <= lastIndex) {
		dfsByInOrder(current * 2);
	}
    
    System.out.print(nodes[current] + " ");

	if ((current*2 + 1) <= lastIndex) {
		dfsByInOrder(current * 2 + 1);
	}
}
...

실행 결과는 아래와 같다.

H D I B E A F C G

다음으로 후위 순회이다. 후위 순회를 구현한 코드는 아래와 같다.

public void dfsByPostOrder() {
	System.out.print("PostOrder : ");
	dfsByPostOrder(1);
	System.out.println();
}

private void dfsByPostOrder(int current) {
	if (current*2 <= lastIndex) {
		dfsByPostOrder(current * 2);
	}

	if ((current*2 + 1) <= lastIndex) {
		dfsByPostOrder(current * 2 + 1);
	}
    
    System.out.print(nodes[current] + " ");
}

실행 결과는 아래와 같다.

H I D E B F G C A

전위 순회는 재귀가 아닌 스택으로도 구현이 가능하다. 아래 코드는 이를 보여준다.

public void dfsByPreOrderUseStack() {
	Stack<Integer> stack = new Stack<>();
	stack.push(1);
		
	int current = 0;
		
	while (!stack.isEmpty()) {
		current = stack.pop();
		System.out.print(nodes[current] + " ");
			
		if ((current*2 + 1) <= lastIndex) {
			stack.push(current * 2 + 1);
		}
			
		if (current*2 <= lastIndex) {
			stack.push(current * 2);
		}
	}
}

이 때는 오른쪽 자식, 왼쪽 자식 순으로 넣어줌으로써 재귀 출력 순서와 동일하게 출력된다.
출력 결과는 아래와 같다.

A B D H I E C F G

알고리즘에서 힙을 활용할 수 있다.

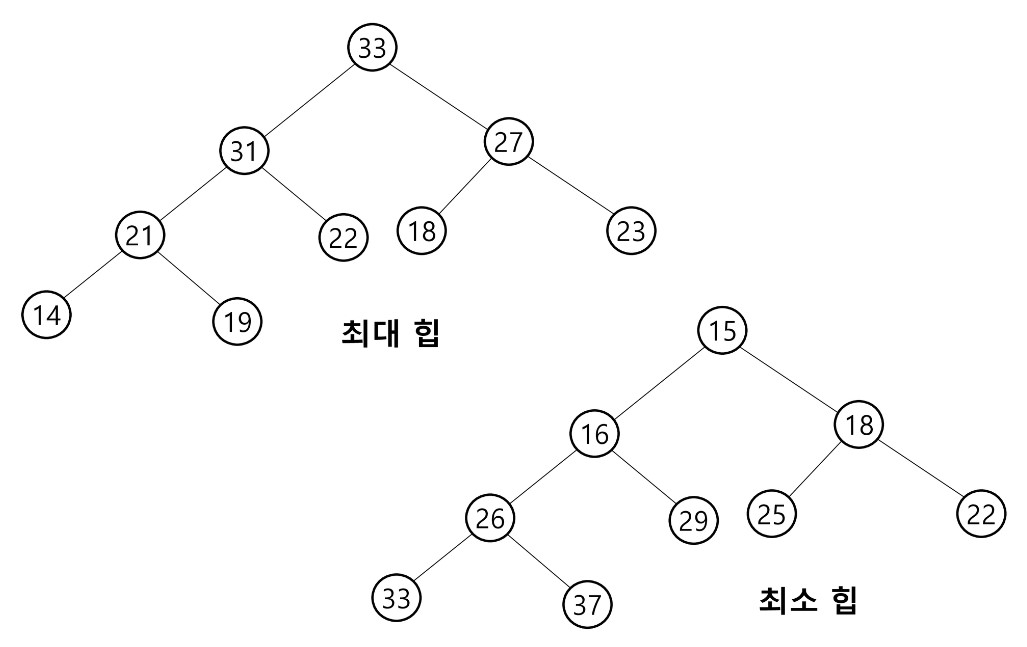
힙은 최대 힙, 최소 힙 두 가지가 있다. 최대 힙의 특징은 아래와 같다.

1. 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리이다.
2. 부모 노드의 키 값 >= 자식 노드의 키 값이 모든 서브 트리에서 성립한다.
3. 2번 논리에 따라 키 값이 가장 큰 노드는 루트 노드가 된다.

최소 힙은 최대 힙과 반대되는 개념이다.

아래 사진은 최대 힙과 최소 힙의 예시이다.