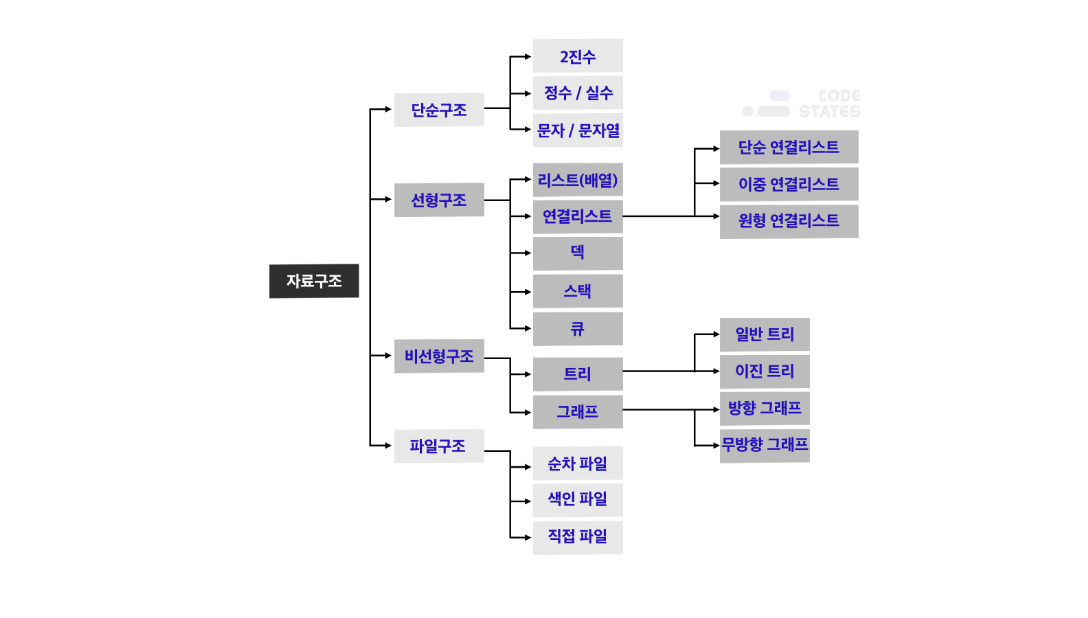
자료구조
데이터를 저장하는 방식.
데이터에 맞는 특성을 지닌 자료구조를 선택하는 것은 효율적인 알고리즘 작성에 반드시 필요하다.
 출처 사진 속에
출처 사진 속에
[선형 자료구조]
한 종류의 데이터가 선처럼 길게 나열된 자료구조
▶ 탐색법 : 순차 탐색, 이진 탐색이 있음
Ⅰ. 랜덤 접근 가능
모든 자료에 O(1)의 시간 복잡도로 접근할 수 있는 자료구조
배열, 해시가 포함된다.
1. 배열(Array) 🔗
▶ 정의
배열 : 같은 타입의 변수들로 이루어진 유한 집합
배열 요소(element) : 배열을 구성하는 각각의 값
인덱스(index) : 배열의 위치를 가리키는 숫자. 0에서 시작한다.
▶ 종류
1차원 배열, 2차원 배열 등
▶ 특징
배열이 차지하는 메모리의 크기 = 배열의 길이 * sizeof(타입);
2. 해시(Hash) 🔗
▶ 정의
해시 : 해시 함수로 구현
해시함수(hash function) : 키와 값으로 구성. 키는 주소를 받고 그 주소에 있는 테이터(값)를 가져오는 방식
▶ 종류
HashTable, HashSet, HastMap, Bloom filter, Dictionary(python)
▶ 특징
O(1)을 보장하지 않는 예외가 있다.
Ⅱ. 랜덤 접근 불가능
모든 자료에 O(1)로 접근이 보장되지 않는 자료구조
1. 스택(Stack) 🔗
▶ 정의
먼저 들어간 자료가 나중에 나오는 LIFO 자료구조.
한쪽 끝에서만 데이터 삽입 삭제 가능
▶연산자(java)
Stack<Integer> st = new Stack<Integer> ();
Deque<Integer> st = new ArrayDeque<Integer>();- push(item) : item 하나를 스택의 가장 윗부분에 추가
- pop() : 스택에서 가장 위에 있는 항목 제거
- peak(), top() : 스택의 가장 위에 있는 항목 반환
- empty() : 스택이 비어 있을 때 true 반환
- search(Object o) : 해당 obj의 위치 반환. top이면 1, 없으면 -1
- size() : 스택에 있는 요소 수 반환
▶ 구현
1. 배열 이용 : 구현이 빠르다. 데이터의 접근 속도가 빠르다. // 크기가 한정적
2. 연결리스트 이용 : 크기 유동적. 삽입 삭제가 용이. // 구현이 어렵다. 조회가 힘들다. 포인터를 위한 추가 메모리 필요
▶ 사용
- 재귀 알고리즘을 반복문을 통해 구현하게 함
- 실행 취소(undo)
- 웹 브라우저 뒤로 가기
- 문자열 역순 출력
2. 큐(Queue) 🔗
▶ 정의
먼저 들어간 자료가 먼저 나오는 FIFO 자료구조.
스택과 반대
▶연산자
Deque<String> qu = new ArrayDeque<String>();- add(item) : item을 큐의 맨 뒤쪽에 추가. 성공 시 true, 공간이 없어 실패하면 예외 발생
- offer(item) : item을 큐의 맨 뒤쪽에 추가.
- peek() : 큐의 맨 앞 데이터를 반환. 큐가 비어있으면 null반환
- element() : 큐의 맨 앞 데이터를 반환
- poll() : 큐의 맨 앞쪽의 데이터 삭제. 해당 요소 반환. 큐가 비어있으면 null 반환
- remove() : 큐의 맨 앞쪽의 데이터 삭제. 해당 요소 반환
▶ 구현
1. 배열 이용 : 구현이 쉽다. 삽입 삭제 용이 // 크기 제한으로 꽉 차면 사용 불가
2. 연결리스트 이용 : 크기가 한정적이지 않음. 원하는 기능 추가 가능 // 구현이 어렵다. 포인터를 위한 추가 공간 필요
▶ 사용
- 작업 또는 데이터를 순서대로 실행/사용할 때
- 비동기 전송
- 너비 우선 탐색 구현
- 프로세스 관리
3. 덱(Deque) 🔗
▶ 정의
스택과 큐를 합친 자료구조
큐의 양쪽 끝에서 삽입과 삭제 가능 (Double-ended Queue)
▶연산자(java)
Deque<String> qu = new ArrayDeque<String>();Queue 인터페이스를 상속받음. Deque 인터페이스를 구현한 LinkedList, ArrayDeque 사용
- addFirst() : 덱의 앞쪽에 데이터 추가. 용량 제한이 있는 덱의 경우 용량을 초과하면 예외가 발생한다.
- addLast() : 덱의 마지막에 데이터 추가. 용량 제한이 있는 덱의 경우 용량 초과 시 예외가 발생한다.
- removeFirst() : 덱의 맨 앞에서 데이터를 뽑아 제거한 다음 해당 데이터를 리턴. 덱이 비어있으면 예외가 발생한다.
- removeLast() : 덱의 마지막에서 데이터를 뽑아 제거한 다음 해당 데이터를 리턴. 덱이 비어있으면 예외가 발생한다.
- getFirst() : 덱의 앞쪽 엘리먼트 하나를 리턴. 덱이 비어있으면 예외가 발생한다
- getLast() : 덱의 맨 뒤쪽 엘리먼트 하나를 리턴. 덱이 비어있으면 예외가 발생한다
- contain(Object o) : 덱에 o와 동일한 데이터가 포함되어 있는지 확인
- size() : 덱의 크기 반환
▶ 구현
1. 배열 이용 : 구현이 매우 복잡함. 큐와 동일
2. 연결리스트 : 큐와 동일
4. 연결 리스트(Linked List) 🔗
▶ 정의
각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식의 자료구조
노드의 포인터가 이전, 다음 노드와의 연결을 담당한다.
▶종류
-
단일 연결 리스트 : 각 노드가 다음 노드만 참조. 가장 단순한 형태 #큐_구현할때 #Head노드_일어버리면_사용불가
-
이중 연결 리스트 : 각 노드가 이전 노드, 다음 노드를 참조. #삭제_간편 #데이터_손상에_강함 #참조2개_작업량_증가
-
원형 연결 리스트 : 연결 리스트에서 마지막 요소가 첫 번째 요소를 참조 #스트림_버퍼_구현할때
▶연산자(java)
LinkedList<String> lnkList = new LinkedList<String>();- add(E e) : 맨 뒤에 전달된 요소를 추가
- add(int index, E e) : 특정 위치에 전달된 요소를 추가
- contains(Object o) : 전달된 객체를 포함하고 있는지를 확인
- get(int index) : 특정 위치에 존재하는 요소를 반환
- isEmpty() : 리스트가 비어있는지를 확인
- remove(Object o) : 리스트에서 전달된 객체를 제거
- remove(int index) : 리스트의 특정 위치에 존재하는 요소를 제거
- size() : 요소의 총개수를 반환
- toArray() : 리스트의 모든 요소를 Object 타입의 배열로 반환
▶ 구현
일반적으로 구조체와 포인터로 구성되기 때문에, 포인터가 없는 java의 경우 포인터 역할을 하는 레퍼런스로 구현한다.
▶ 연결리스트와 배열의 차이점
| 배열 | 연결 리스트 | |
|---|---|---|
| 장점 | - 값마다 인덱스를 가지기 때문에 탐색에 유리하다. | - 데이터를 삽입 또는 삭제할 때 노드만 바꿔서 연결해주면 된다. - 크기가 가변적이다. |
| 단점 | - 값마다 인덱스를 가지기 때문에 삽입이나 삭제에 불리하다. - 크기가 정해져 있어 가득 차면 사용할 수 없다. | - 데이터의 조회가 힘들다. 각 데이터에 한번에 접근할 수가 없어서 순차적으로 접근해야된다. |
[비선형 자료구조]
선형이 아닌 모든 자료구조. i번째 값을 탐색한 뒤 i+1이 정해지지 않은 구조
1. 그래프(Graph)🔗
▶ 정의
-
그래프 : 연결되어 있는 객체 간의 관계를 표현한 자료구조. 정점과 간선으로 이루어져 있으며, 정점마다 간선이 있을 수도 없을 수도 있다.
-
정점(vertex) : 위치라는 개념. node라고도 부름
-
간선(edge) : 위치 간의 관계. 즉, 노드를 연결하는 선. link, branch라고도 부름
-
인접 정점 : 간선에 의해 직접 연결된 정점
-
차수 : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
-
진입 차수(내차수) : 방향 그래프에서 외부에서 오는 간선의 수
-
진출 차수(외차수) : 방향 그래프에서 외부로 향하는 간선의 수
-
경로 길이 : 경로를 구성하는 데 사용된 간선의 수
-
단순 경로 : 반복되는 정점이 없는 경로 (한붓그리기)
-
사이클 : 단순 경로의 시작과 종료 정점이 동일한 경우
▶ 구현
-
배열(인접 행렬 방식) : 그래프의 노드를 2차원 배열로 만든 것. 노드 간 직접 연결되어 있으면 1, 아니면 0으로 행렬 완성
-
연결리스트(인접 리스트 방식) : 노드를 리스트로 표현한 것. 정점의 리스트 배열을 만들어 관계를 설정. 노드들 간에 직접 연결되어 있으면 해당 노드의 인덱스에 그 노드를 삽입
▶종류
- 무방향 그래프 : 두 정점을 연결하는 간선에 방향이 없음
- 방향 그래프 : 두 정점을 연결하는 간선에 방향이 존재
- 연결 그래프 : 모든 노드들이 간선에 의해 연결됨. 무방향 그래프의 모든 정점 쌍이 항상 경로가 있음. #예)트리
- 비연결 그래프 : 무방향 그래프이며 간선에 의해 연결되지 않은 노드가 있다.
- 완전 그래프 : 그래프의 모든 정점이 서로 직접 연결
- 순환 그래프 :단순 경로에서 시작 정점과 도착 정점이 동일
- 비순환 그래프 : 사이클이 없음
▶ 알고리즘
순회 및 탐색 : 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
2. 트리 🔗
▶ 정의
트리(Tree) : 계층적인 자료를 표현하는데 이용되는 자료구조. 그래프의 한 종류이다.
노드(Node) : 그래프의 정점
- 루트 노드 : 트리의 기준이 되는 노드. 나무의 뿌리를 생각하면 된다. 루트 노드에서 가지가 뻗어나가는 이미지.
- 부모 노드 : 자신과 인접한 노드들 중 루트 노드로 향하는 노드
- 자식 노드 : 자신과 인접한 노드들 중 루트 노드의 반대 방향으로 향하는 노드
- 단말 노드 : 자식 노드가 존재하지 않는 노드. 가지의 끝
- 형제 노드 : 부모 노드가 같은 노드
-
가지(Branch) : 그래프의 간선. 트리에서는 양방향 간선만 사용한다.
-
부트리(Sub Tree) : 부분 그래프와 비슷하게 정의한다.
-
차수(Degree) : 자식 노드의 개수.
-
길이(Length) : 임의의 두 노드를 시작 노드, 도착 노드로 하는 경로에서 거치게 되는 노드의 수.
-
깊이(Depth) : 루트 노드에서 해당 노드까지의 길이.
- 레벨(Level) : 깊이가 같은 노드의 집합.
- 높이(Height) : 가장 깊이가 깊은 단말 노드까지의 길이. 깊이 중 최댓값
▶종류
일반 트리 : 이진트리가 아닌 모든 트리
이진 트리 : 각 노드가 최대 두 개의 자식을 갖는 트리. 모든 노드의 차수가 2 이하
- 전 이진 트리(Full Binary Tree) : 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
- 포화 이진 트리(Perfect Binary Tree) : 모든 단말 노드의 깊이가 같은 이진트리
- 완전 이진 트리(Complete Binary Tree) : 모든 단말 노드의 깊이의 최댓값과 최솟값의 차이가 0 또는 1인 이진트리. 즉, 트리의 원소를 왼쪽에서 오른쪽으로 하나씩 빠짐없이 채워나간 형태이다.
- 이진 탐색 트리(Binary Search Tree) : 모든 노드가
[ 모든 왼쪽 자식들 < n < 모든 오른쪽 자식들 ]의 특징을 가지는 이진 트리. 같은 값을 가지는 노드는 없다.
▶ 알고리즘
이진 트리 순회 알고리즘 : 전위 순회, 중위 순회, 후위 순회, 레벨 순서 순회가 있다.
이진 탐색 알고리즘 : 이진 탐색 트리일 때만 탐색 가능 루트 노드부터 방문하여 찾는 값이 작으면 왼쪽, 크면 오른쪽을 방문하며 값을 찾는다.
▶ 구현
1. 배열(인접 행렬 방식) : 1차원 배열에 자신의 부모 노드만 저장, 2차원 배열에 자식 노드를 저장
2. 리스트(인접 리스트 방식) : ArrayList 컬렉션 또는 배열로 구현
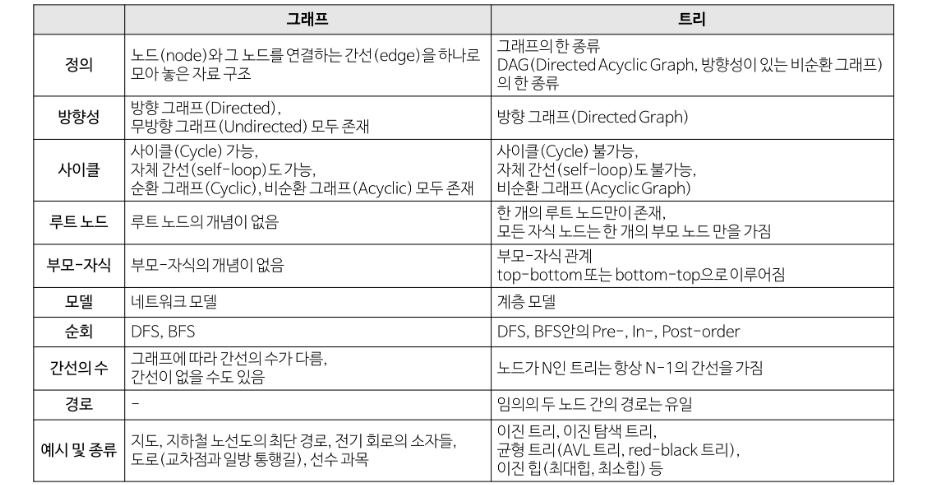
▶ 그래프와 트리의 차이
3. 힙(Heap) 🔗
▶ 정의
힙 : 완전 이진트리의 일종. 우선순위 큐를 위해 만들어진 자료구조이다. 반 정렬 상태를 유지. 중복 값을 허용.
우선순위 큐 : 우선순위의 개념을 큐에 도입. 데이터들이 우선순위를 가져서 우선순위가 높은 데이터가 먼저 나간다.
반 정렬 상태 : 어려 값 중에서 최댓값과 최솟값을 빠르게 찾도록 만들어진 자료구조.
▶종류
-
최대 힙 : 부모 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리
-
최소 힙 : 부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리. 최대 힙과 반대
▶ 구현
배열로 구현 : 제일 위 레벨부터 왼쪽에서 오른쪽으로 하나씩 배열에 삽입. 부모와 자식을 인덱스로 찾기 쉽다.
▶ 사용
- 우선순위 큐의 구현
- 힙 정렬
- 허프만 코드
- 운영 체제의 작업 스케쥴링
