해시 테이블이란?
키-값 쌍(key-value pair)을 저장하기 위한 자료 구조
배열과 유사한 구조를 가지고 있으며, 키(key)를 인덱스(index)로 사용하여 값을 저장하고 검색 가능
해시 함수(hash function)를 사용하여 키(key)를 배열 인덱스(index)로 변환함
해싱 구조로 데이터를 저장하면 Key값으로 데이터를 찾을 때 해시 함수를 1번만 수행하면 되므로 매우 빠르게 데이터를 저장/삭제/조회할수 있음
시간복잡도 : 평균 O(1), 하지만 데이터의 충돌이 발생한 경우 Chaining에 연결된 리스트들까지 검색을 해야 하므로 O(N)까지 시간복잡도가 증가할 수 있음
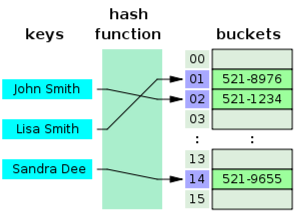
해시 함수?
임의의 길이의 입력을 받아, 고정된 길이의 출력을 생성하는 함수
해시 함수에서 중요한 것은 고유한 인덱스 값을 설정하는 것.
[대표적인 해시 함수]
- Division Method: 나눗셈을 이용하는 방법으로 입력값을 테이블의 크기로 나누어 계산한다.( 주소 = 입력값 % 테이블의 크기) 테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 알려져 있다.
- Digit Folding: 각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다.
- Multiplication Method: 숫자로 된 Key값 K와 0과 1사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같은 계산을 해준다. h(k)=(kAmod1) × m
- Univeral Hashing: 다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법이다.
해시 충돌이 발생하는 이유
서로 다른 두 개의 입력이 같은 출력 값을 생성한다면, 이를 해시 충돌(hash collision)이라고 함
해시 충돌 해결 방법
-
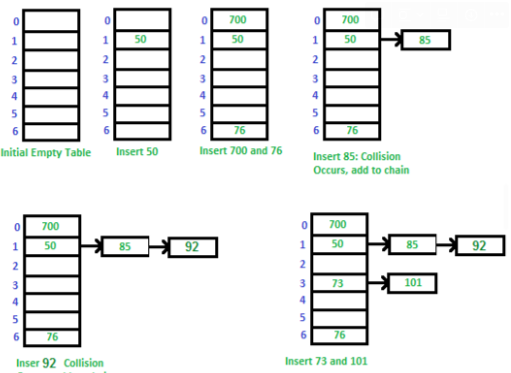
분리 연결법(separate chaining)
해시 충돌이 발생하면, 해당 인덱스에 연결 리스트(linked list)를 생성하여 값을 저장함. 각 연결 리스트는 각기 다른 해시 충돌 그룹을 관리함
public class Node {
private int key;//키
private String value; //값
private Node next;
public Node(int key, String value) {
this.key = key;
this.value = value;
}
public int getKey() {
return key;
}
public void setKey(int key) {
this.key = key;
}
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}
public class HashTable {
private int size; //현재 해시 테이블에 저장된 요소의 개수
private Node[] table;
public HashTable(int size) {
this.size = size;
table = new Node[size];
}
public int hashFunction(int key) {
return key % size;
}
public void insert(int key, String value) {
int index = hashFunction(key);
Node node = table[index];
// 버킷이 비어있는 경우
if (node == null) {
table[index] = new Node(key, value);
return;
}
// 이미 값이 존재하는 경우
while (node != null) {
// 기존 값과 키가 일치하는 경우, 값을 갱신
if (node.getKey() == key) {
node.setValue(value);
return;
}
// 연결 리스트의 끝까지 탐색한 경우, 새로운 노드 추가
if (node.getNext() == null) {
node.setNext(new Node(key, value));
return;
}
node = node.getNext();
}
}
public String search(int key) {
int index = hashFunction(key);
Node node = table[index];
while (node != null) {
if (node.getKey() == key) {
return node.getValue();
}
node = node.getNext();
}
return null;
}
public void delete(int key) {
int index = hashFunction(key);
Node node = table[index];
Node prev = null;
while (node != null) {
if (node.getKey() == key) {
// 첫 번째 노드인 경우
if (prev == null) {
table[index] = node.getNext();
} else {
prev.setNext(node.getNext());
}
return;
}
prev = node;
node = node.getNext();
}
}
}-
개방 주소법(open addressing)
다른 빈 인덱스를 찾아서 값을 저장함. 선형 탐사(linear probing)나 이차 탐사(quadratic probing), 이중 해싱(double hashing) 등의 방법이 사용됨
- 선형 탐사(Linear Probing)
- 충돌이 발생한 경우에, 다음 인덱스로 이동하여 빈 공간을 찾는 방식
h인 인덱스에 이미 다른 요소가 저장되어 있는 경우, 선형 탐사는h + 1,h + 2,h + 3, ... 순서로 다음 인덱스를 검사하여 빈 공간을 찾음
- 제곱 탐사(Quadratic Probing)
- 제곱 값을 이용하여 다음 인덱스로 이동하여 빈 공간을 찾는 방식
- 이중 해싱(Double Hashing)
- 다른 해시 함수를 사용하여 다음 인덱스로 이동하여 빈 공간을 찾는 방식
- 해시 값이
h1인 인덱스에 이미 다른 요소가 저장되어 있는 경우, 이중 해싱은h1 + i * h2순서로 다음 인덱스를 계산하여 검사합니다. 여기서h2는 다른 해시 함수를 사용하여 계산한 값이며,i는 충돌이 발생한 횟수
public class OpenAddressingHashMap<K, V> { private int capacity; // 해시테이블의 크기 private int size; // 해시테이블에 저장된 데이터 개수 private K[] keys; // 키를 저장하는 배열 private V[] values; // 값(Value)을 저장하는 배열 // 해시테이블 초기화 public OpenAddressingHashMap(int capacity) { this.capacity = capacity; this.size = 0; this.keys = (K[]) new Object[capacity]; this.values = (V[]) new Object[capacity]; } // 해시 함수: key의 해시 값을 반환 private int hash(K key) { return Math.abs(key.hashCode()) % capacity; } // 데이터 추가 public void put(K key, V value) { if (size == capacity) { throw new RuntimeException("HashMap is full."); } int index = hash(key); //선형 탐사 while (keys[index] != null) { if (keys[index].equals(key)) { values[index] = value; return; } index = (index + 1) % capacity; } keys[index] = key; values[index] = value; size++; } // 데이터 조회 public V get(K key) { int index = hash(key); while (keys[index] != null) { if (keys[index].equals(key)) { return values[index]; } index = (index + 1) % capacity; } return null; } // 데이터 삭제 public void remove(K key) { int index = hash(key); while (keys[index] != null) { if (keys[index].equals(key)) { keys[index] = null; values[index] = null; size--; return; } index = (index + 1) % capacity; } } // 데이터 개수 조회 public int size() { return size; } // 해시테이블이 비어있는지 확인 public boolean isEmpty() { return size == 0; } }
- 선형 탐사(Linear Probing)
HashMap(해시맵)과 HashTable(해시테이블) 차이
- 동기화(synchronization) 지원 여부
- HashTable은 모든 메서드가 동기화(synchronized)되어 있어, 멀티스레드 환경에서 안전하게 사용할 수 있음. 하지만, 이러한 동기화로 인해 성능이 떨어지는 단점 존재
- HashMap은 멀티스레드 환경에서 안전하지 않으며, 동기화를 위한 추가적인 오버헤드가 발생하지 않음. 그러나 멀티스레드 환경에서 안전하게 사용하기 위해서는 별도의 동기화 처리가 필요함.
- null 값 허용 여부
- HashTable은 key와 value 모두 null 값을 허용하지 않음. 따라서, null 값을 key나 value로 사용할 수 없음
- HashMap은 key와 value 모두 null 값을 허용
- 성능
- Hashtable은 모든 메서드가 동기화되어 있어, 멀티스레드 환경에서 안전하게 사용할 수 있지만, 성능이 떨어지는 단점이 있음
- HashMap은 단일 스레드 환경에서 성능이 더 우수합니다. 멀티스레드 환경에서는 동기화 처리를 위한 추가적인 오버헤드가 발생할 수 있기 때문에 성능이 떨어질 수 있음
