Sorting

• To sort an array in an order

Types of sorting

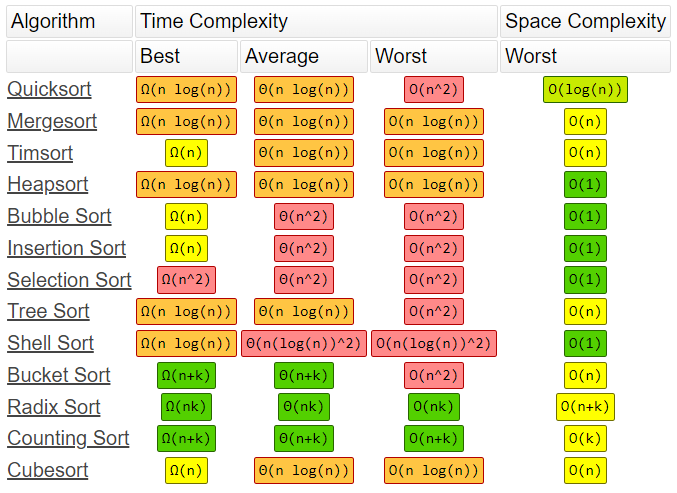
Complexity of types of sorting

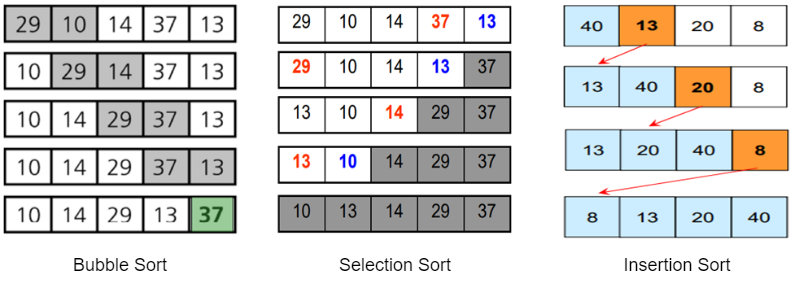
Bubble Sort 버블 정렬

1. Swaps two consecutive elements to order until no more swaps occur

• Has a time complexity of O(N^2)

def bubble_sort(array):
    n = len(array)
    ans = []

    for i in range(n-1):
        # For i = 0 and n = 5, n-i-1 = 4
        # Last element does not need to be evaluated,
        # then the second to last element, and so on
        for j in range(n-i-1):
            # Evaluate the current element and the next element
            if array [j] > array[j+1]:
                # If the next element is smaller, then swap
                array[j], array[j+1] = array[j+1], array[j]
    return array

Selection Sort 선택 정렬

1. Selects the smallest element in the array, then places it to the first index
2. Repeat with the rest of the elements

• Has a time complexity of O(N^2)

def selection_sort(array):
    n = len(array)
    
    for i in range(n-1):
        minIndex = i
        # The ith (1st, 2nd, etc.) element
        # does not need to be evaluated
        # after switching elements
        for j in range(n-i):
            # If i = 0 and j = 1, evaluate if array[1] is smaller than [0]
            # If i = 0 and j = 2, evaluate if array[2] is smaller than [0]
            # So i+j evaluates all values after ith element
            if array[i+j] < array[minIndex]:
                # Swap values if array[i+j] is smaller than array[i]
                # Swap occurs once, so this determines the index of the smallest value
                # then swap outside the for j loop
                minIndex = i+j
                array[i], array[minIndex] = array[minIndex], array[i]
    return array

Insertion Sort 삽입 정렬

1. Compares the current element with the next element.
2. If the next element is smaller, then all the elements to the left are compared.
3. The smaller element swaps places one by one with larger elements to the left.

• Has a time complexity of O(N^2)

def insertion_sort(array):
    n = len(array)

    # The first element does not need to be evaluated
    for i in range(1, n):
        # Loops through all elements to the
        # left of the element i
        for j in range(i):
            # If i = 2, then j is 0 or 1
            # i-j = 2 or 1 and i-j-1 = 1 or 0
            # This is because the current element must
            # compare each element to the left and swap one by one
            if array[i-j] < array[i-j-1]:
                array[i-j], array[i-j-1] = array[i-j-1], array[i-j]
            # If the current element is bigger, break
            # and evaluate the next element to the right
            else:
                break
    return array

Merge 병합

Merge and sort two sorted arrays.

• Has a time complexity of O(N), since array1 and array2 create an array of length N

1. Create two variables that track the index of the arrays
2. If arrayA[0] is smaller than arrayB[0], then append arrayA[0] to arrayAns and increase arrayAIndex by 1
3. The next loop would compare arrayA[1] to arrayB[0] and so on
4. If there is a leftover element in arrayA or arrayB, append the last element to arrayAns

def merge(array1, array2):
    array = []
    array1Index = 0
    array2Index = 0
    while array1Index < len(array1) and array2Index < len(array2):
        if array1[array1Index] < array2[array2Index]:
            array.append(array1[array1Index])
            array1Index += 1
        else:
            array.append(array2[array2Index])
            array2Index += 1
            
    # If there is a leftover element in array 2
    if array1Index == len(array1):
        while array2Index < len(array2):
            array.append(array2[array2Index])
            array2Index += 1

    # If there is a leftover element in array 1
    if array2Index == len(array2):
        while array1Index < len(array1):
            array.append(array1[array1Index])
            array1Index += 1
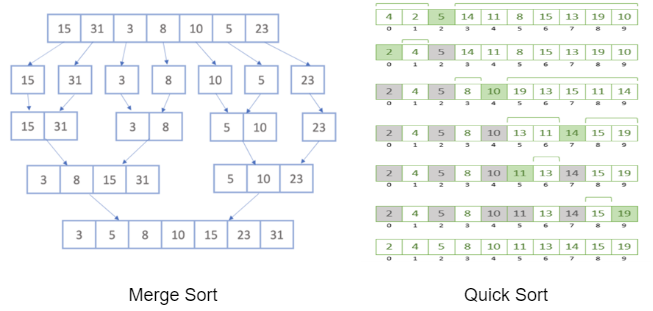
    return array

Merge Sort 병합 정렬

Uses the concept from the merge function above to sort an array.
Merge Sort uses the concept called Divide and Conquer (분할 정복).

• Splits the array into N/2^k times, where k is the number of times needed to divide the array into single arrays.
  - N/2^k = 1, therefore k = log2N. Each kth process has a time complexity of O(N) (due to the merge function above)
  - This gives the time complexity of log2N O(N), or **O(N logN)**

1. Separates the array into halves until the elements are coupled
2. The two couples are sorted, then merged with another couple
3. The merged group is sorted, then so on until the entire array is merged again

For an array of length N, MergeSort(0,N) should run Merge(MergeSort(0, N/2) + MergeSort(N/2,N)).
This behavior is recursive.

def merge_sort(array):
    # 탈출 조건
    # A single array is already "sorted"
    if len(array) <= 1:
        return array

    # Get the middle index of the array
    mid = len(array) //2
    
    # Recursively run merge_sort
    leftArray = merge_sort(array[:mid])
    rightArray = merge_sort(array[mid:])

    return merge(leftArray, rightArray)