들어가며
지난 학기 수치해석이라는 강의를 들었는데, 5년이라는 꽤나 긴 대학생활 중 가장 재미있게 들었던 강의였다.
수치해석이란 우리의 실생활을 물리 법칙으로 표현하여 근사하는 학문으로 관측하기 어려운 공간, 시간에 대해서 물체가 어떻게 변화할 지 예측하는 것을 목표로 한다.
이미 근사를 넘어 생성, 분류, 멀티 모달까지 수행할 수 있는 인공지능 모델들이기에 '수치해석을 인공지능으로 수행할 수 있지 않을까?' 라는 생각을 하게 되었고 실제로 PINN(Physics Informed Neural Network)이라는 분야로 활발한 연구가 이루어지고 있었다.
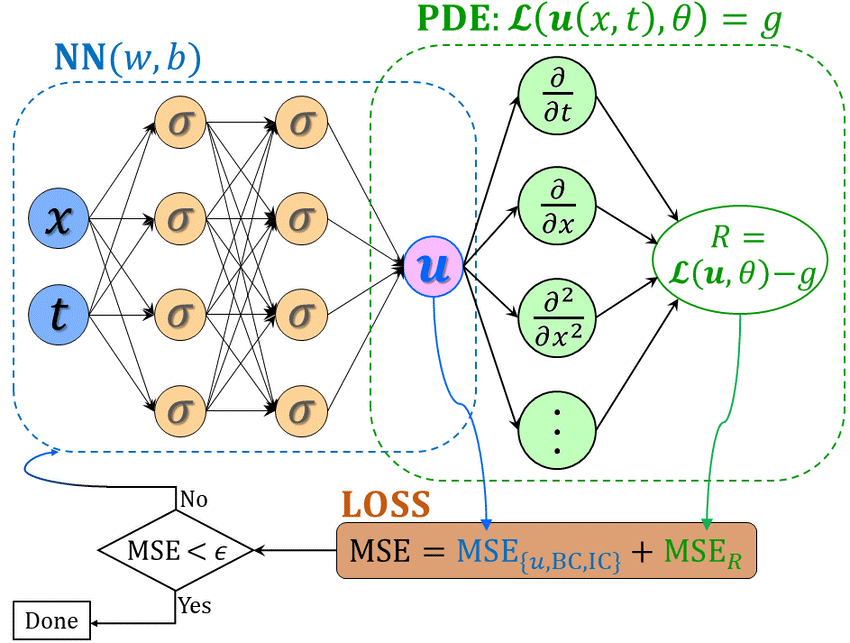
Physics Informed Neural Network
이름에서도 알 수 있듯이 물리 법칙을 뉴럴 넷에 넣어 모델이 물리 법칙을 만족하면서 추론할 수 있게 하는 인공지능이다. 물리 법칙은 주로 손실함수나 규제를 통해 뉴렐 넷에 들어간다.
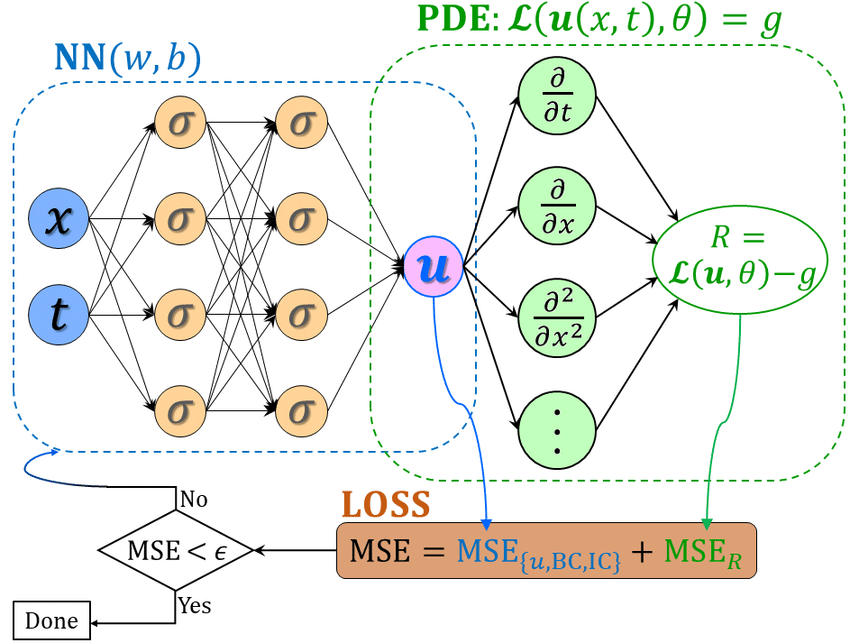
PINN은 위 두가지 분야에 큰 장점을 갖고 있기 때문에 공학 분야에 큰 적용 가능성을 갖고 있다.
- 데이터 없이 학습이 가능하다
- 외삽에 강하다
먼저 공학 분야의 경우 양질의 데이터 수집이 굉장히 어려워 인공지능이 적용되기 어렵다는 한계점이 존재했었다. SSL, Zero-shot 등 적은 데이터로도 좋은 성능을 내는 다양한 모델들이 있지만 공학 분야는 일반적인 인공지능 테스크보다 결과값이 더 엄밀해야하기 때문에 활용하기 어려웠다. PINN의 경우 물리 법칙과 경계조건이 명확한 경우 학습에 데이터 셋 대신 collocation point를 사용한다. 즉, 학습 데이터 셋 수집이 불필요하다는 것이다. 또한 물리 법칙이 불완전한 경우 (ex. 미지의 탄성계수) 적은 수의 데이터 셋과 collocation point를 이용해 물리 미분 방정식을 추론할 수 있다는 장점이 있다.
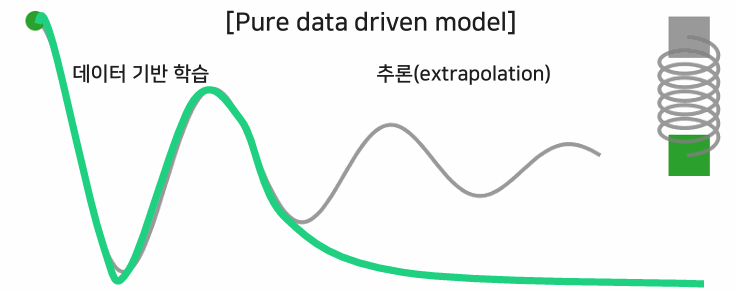
공학 분야에 근사, 추론을 사용하는 이유는 일반적인 상태를 알고 싶어서가 아닌 극단적인 경우를 예측하고 시뮬레이션하고 있어서인 경우가 많다. (최악의 상황을 알아야 이를 대비하니까..!) PINN은 갖고 있는 데이터 이후의 추론에도 물리 법칙을 만족하도록 모델링 되기 때문에 외삽에 강하다.
Task : Spring two-Mass System

본 문제는 Spring Mass System으로 두개의 질량체와 스프링이 있을 때 주어진 초기, 경계 조건에 따라 질량체 m1, m2가 어떻게 거동할지를 시뮬레이션하는 문제이다.
본 문제의 지배 방정식은 다음과 같다.
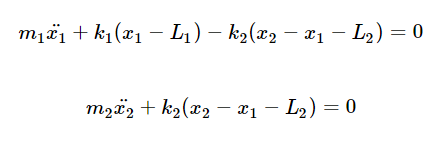
Base Model
본 문제를 해결하기 위해 classifier 모델로 3개의 FC-layer로 이루어져 있는 매우 간단한 모델 구조를 사용했다.
class FCN(nn.Module):
"Defines a fully-connected network in PyTorch"
def __init__(self, N_INPUT, N_OUTPUT, N_HIDDEN, N_LAYERS):
super().__init__()
activation = nn.Tanh
self.fcs = nn.Sequential(*[
nn.Linear(N_INPUT, N_HIDDEN),
activation()])
self.fch = nn.Sequential(*[
nn.Sequential(*[
nn.Linear(N_HIDDEN, N_HIDDEN),
activation()]) for _ in range(N_LAYERS-1)])
self.fce = nn.Linear(N_HIDDEN, N_OUTPUT)
def forward(self, x):
x = self.fcs(x)
x = self.fch(x)
x = self.fce(x)
return x 해결 과제가 간단하기 때문에 보다 간단한 구조로도 해결이 가능함을 보이고 싶었다.
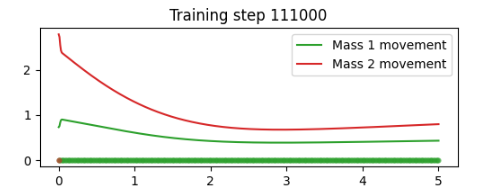
하지만 결과가 잘 나오지 않았는데, 그 이유로
- 지배 방정식의 일계, 이계도함수 값에 문제가 있다
- Optimizer, learning rate 등 fine-tuning에 대한 문제이다
를 생각할 수 있었다.
학습 문제 해결 1 : Jacobian, hessian matrix 사용
보통 torch 기울기를 구할 때
torch.autograd.grad를 많이 이용한다.
그래서 Base model을 학습 시킬 때 일계도함수, 이계도함수 모두 autograd.grad를 이용하여 구하였는데 이 과정에서 문제가 생긴 것이라고 생각했다. 그 이유로 본 과제는 t라는 하나의 input으로 displacement_m1, displacement_m2라는 두개의 output을 추론해야하는데 이 때 많은 문제가 발생했다. (특히 이계도함수를 구할 때)
그래서 보다 원론적인 행렬 기능을 사용하기로 했는데 그래서 사용한 방법이 야코비 행렬과 헤시안 행렬이다.
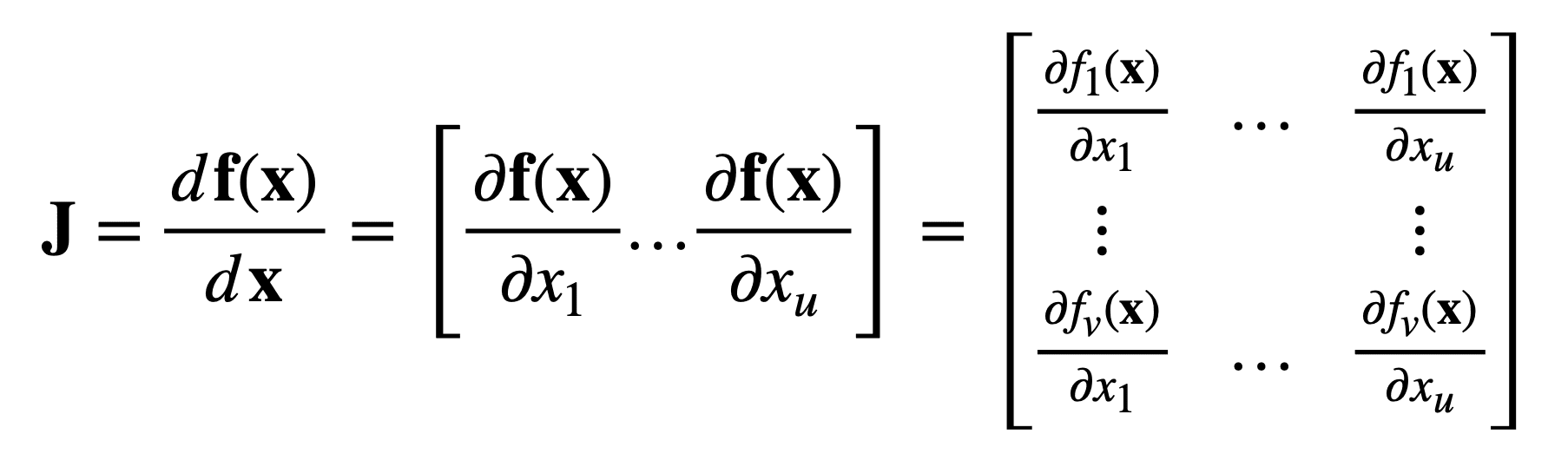
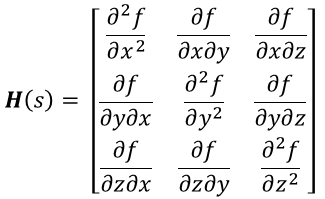
pytorch에도 위 행렬을 계산해주는 함수가 존재했고 이를 이용해 새롭게 지배방정식을 계산, 학습하려고 했다.
하지만 헤시안 행렬은 사용할 수 없었는데, 헤시안 행렬의 경우 output 하나에 대해서 input들의 이계도함수를 행렬로 표현해주기 때문에 우리가 해결해야하는 문제와 성격이 맞지 않았다.
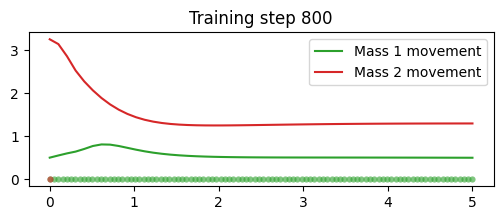
이계도함수를 구하기 위해
- jacobian matrix의 값을 autograd.grad에 넣기
- jacobian matrix를 두번 수행하기
를 시도해보았다.
하지만 결과적으로 학습이 잘 진행되지 않았으며 잘 나온다고 해도 구현된 코드가 이계도함수에 맞는 코드인지 알 수 없었기에 결국 기초적인 수치적 해석 방법인 도함수의 정의를 이용해 이계도함수 값을 근사하기로 했다.
학습 문제 해결 2 : LBFGS Optimizer 사용
LBFGS Optimizer는 경계조건이 있고, 여러 차원(고계도함수) 학습에 효과적인 optimizer이다. 실제로 함께 PINN에 대해 공부하는 친구가 Buckling에 대한 모델을 구현했는데, Adam을 이용했을 때에는 학습이 잘 이루어지지 않았지만 LBFGS를 이용했을 때 훨씬 빠르게 참값에 수렴했다라는 경험을 말해주었다. 본 문제에 대해서도 학습이 잘 이루어지지 않는 이유가 Optimizer에 있지는 않을까 싶어 Adam 대신 LBFGS를 사용하여 학습을 진행해보았다.
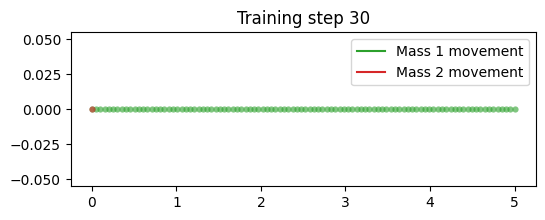
하지만 학습이 잘 진행되지 않고 학습을 진행할수록 결과값이 nan이 나오는 문제가 있었다. 이에 대한 추가적인 공부가 필요할 듯 하다.
학습 문제 해결 3 : 수치해석적 접근
이계도함수를 구하는 방법으로 가장 확실한 도함수의 정의를 이용하였다. 근사할 h 값을 설정하여 f(a), f(a+h), f'(a), f'(a+h)을 구하고 이를 기반으로 f''(a)값을 구해주었다.
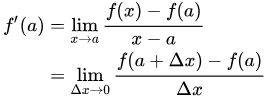
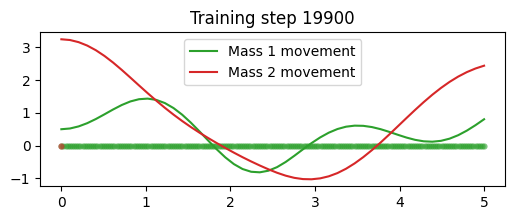
그 결과 학습이 잘 이루어졌으며 실제 거동 값과도 매우 유사한 추론을 보였다.
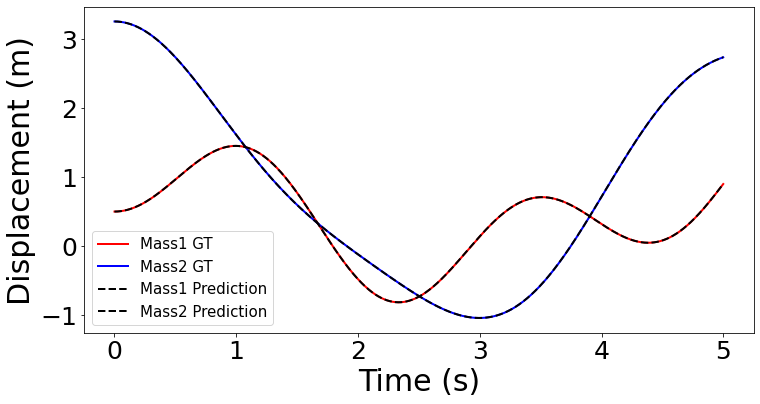
결과 및 논의점
PINN의 가장 큰 장점은 데이터 셋 없이 물리법칙을 만족하는 모델을 구축할 수 있다는 것이다. 본 문제의 경우도 collocation point 100개 만으로 꽤나 smooth한 모델을 구축하였다. 다만 본 문제의 경우 도함수의 정의를 통해 고계도함수를 근사하였는데, 모델을 학습할 때 이를 미세한 차이의 두 output으로 기울기를 근사하는 것이기 때문에 값을 model에 값을 두번 통과시켜야한다는 단점이 존재한다. 앞으로의 모델링에는 최대한 jacobian, hessian matrix, autograd를 활용해야할 것이다.
- 행렬, pytorch library에 대한 추가적인 공부를 통해 고계도함수를 구하는 확실한 방법을 익힌다
- LBFGS Optimizer에 대한 추가적인 공부와 적용이 필요하다
- PINN의 핵심은 Neural Net보다 적용하고 싶은 분야의 domain 지식이다. 건설 분야에 대한 PINN을 구축해보자.
