Graph

이 글에선 Graph, Tree, Binary Search Tree에 최소한의 알아야 할 정보들을 기록한다.

Graph (그래프)

---

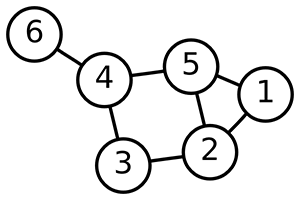
특징

• 상하위의 구분없이 노드와 노드를 연결하는 간선을 하나로 모아 놓은 자료구조.
• 그래프의 목적 : 연결되어 있는 객체 간의 관계 표현
  • EX) 지도, 지하철 노선도의 최단 경로, 도로(교차점과 일방 통행길) 등
• 그래프는 부모 - 자식, 루트 노드 개념이 없고 방향 그래프, 무방향 그래프 개념이 존재한다.
  • 방향 그래프 : 간선에 방향성이 존재한다. A -> B 로만 갈 수 있는 간선은 <A, B>로 표시.
  • 무방향 그래프 : 간선을 통해 양방향으로 이동한다. A 와 B 를 연결하는 간선은 (A, B)로 표시

그래프와 관련된 용어

• 정점 (node) : 위치 (vertex 라고도 부름)
• 간선 (edge) : 노드를 연결하는 선 (link 라고도 부름)
• 인접 정점 (adjacent vertex) : 간선에 의해 직접 연결된 정점
• 정점의 차수 (degree) : 정점과 연결된 간선의 수
  • 진입 차수 (in-degree) : 외부에서 오는 간선의 수
  • 진출 차수 (out-degree) : 내부에서 외부로 향하는 간선의 수

그래프 구현 방법

• 그래프 구현은 인접 리스트로 구현과 인접 행렬로 구현하는 방법이 있다.
  • 인접 리스트 (Adjacency List) : 각각의 노드에 인접한 노드 리스트를 입력하는 방법

{
  A: [B, C],
  B: [A, C],
  C: [A, B]
}

• 인접 행렬 (Adjacency Matrix) : 이 방식은 노드를 이중 배열에 담는 방식이다. 이 후 노드가 연결되어 있다면 matrix[i][j] = 1, 연결이 안 되어 있다면 matrix[i][j] = 0 으로 두는 방식이다.

인접 리스트와 인접 행렬 장단점

• 인접 리스트
  • 장점
    • 어떤 노드의 인접한 노드를 쉽게 찾는다.
  • 단점
    • 최악의 경우 노드 리스트 안에 있는 노드들을 다 순회해야한다.
• 인접 행렬
  • 장점
    • 두 노드를 연결하는 간선의 존재 여부를 (matrix[i][j]) 바로 알 수 있다.
  • 단점
    • 어떤 노드에 인접한 노드들을 찾기 위해 모든 노드를 순회해야 한다.

인접 리스트를 이용한 그래프 구현

class Graph {
  constructor() {
    this.adjacencyList = {};
  }

  addVertex(vertex) {
    if (!this.adjacencyList[vertex]) {
      this.adjacencyList[vertex] = [];
      return true;
    }
    return false;
  }

  addEdge(vertex1, vertex2) {
    if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
      this.adjacencyList[vertex1].push(vertex2);
      this.adjacencyList[vertex2].push(vertex1);
      return true;
    }
    return false;
  }

  removeEdge(vertex1, vertex2) {
    if (this.adjacencyList[vertex1] && this.adjacencyList[vertex2]) {
      this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
        (v) => v !== vertex2
      );
      this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
        (v) => v !== vertex1
      );
      return true;
    }
    return false;
  }

  removeVertex(vertex) {
    if (!this.adjacencyList[vertex]) return undefined;
    while (this.adjacencyList[vertex].length) {
      let temp = this.adjacencyList[vertex].pop();
      this.removeEdge(vertex, temp);
    }
    delete this.adjacencyList[vertex];
  }
}