Tree

Tree

---

트리의 개념

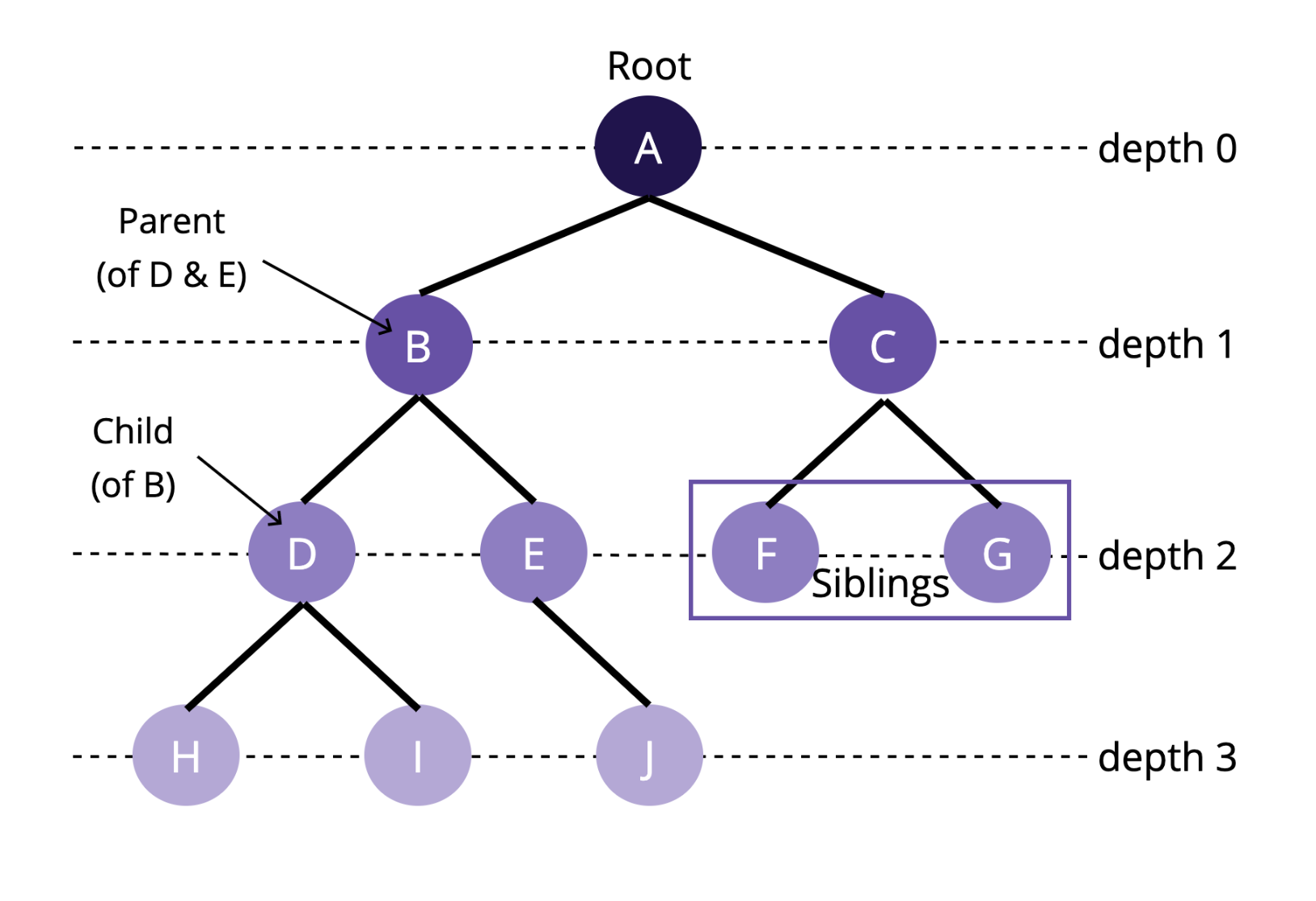
• 트리는 노드로 이루어진 계층적 자료구조.

관련 용어

• 노드(node): A, B, C 등 트리의 구성 요소. 정점(vertex) 라고도 부른다.
• 루트 노드(root node): A와 같이 트리 최상위에 위치한 노드. 트리에선 하나의 루트 노드를 가진다.
• 단말 노드(leaf node): H, I, F, G 등 자식이 없는 최하위에 위치한 노드. 외부 노드(external node) 라고도 부른다.
• 내부 노드(internal node): 하나 이상의 자식 노드를 가진 노드
• 간선(edge): 각각의 노드를 연결하는 선을 의미한다.
• 형제(sibling): 같은 부모를 갖고 있는 노드를 의미한다.
• 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
• 노드의 깊이(depth): 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
• 노드의 차수(degree): 각 노드가 지닌 간선의 수
• left node: 자식이 없는 node

특징

• 그래프의 한 종류다.
• 부모 - 자식으로 이루어진 계층 구조다.
• 방향 그래프이자 비순환 그래프다. (여기서 비순환은 루트 노드로 다시 돌아가지 않는 것을 의미)
• 루트 노드는 0개 이상의 자식 노드를 갖고 있다. 마찬가지로 자식 노드도 0개 이상의 자식 노드를 갖고 있다.

종류

• 트리에는 이진 트리(Binary Tree)가 존재한다.
  

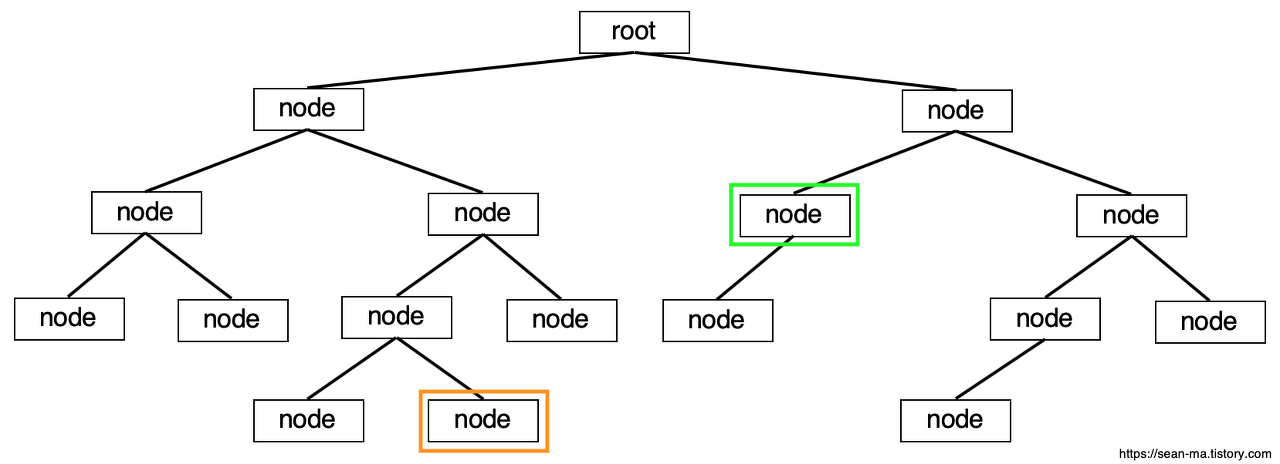
• 이진 트리: 각 노드가 최대 두 개의 자식을 갖는 트리

  • 왼쪽 자식을 left subtree, 오른쪽 자식을 right subtree라고 한다.

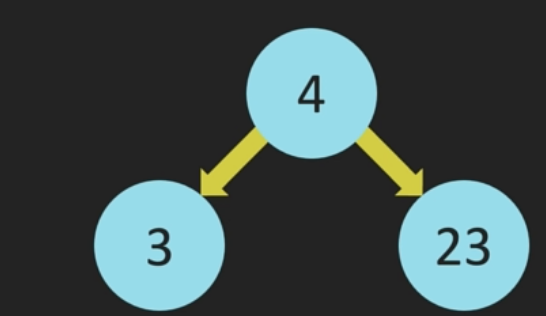
  • 이진 트리에는 정 이진 트리(full binary tree), 완전 이진 트리(complete binary tree), 포화 이진 트리(perfect binary tree)가 있다.

    1. 정 이진 트리(full binary tree): 각 내부 노드가 0 개 혹은 두 개의 자식 노드를 갖는 순서화된 트리 (짝수 개의 자식 노드를 갖는다.)
       
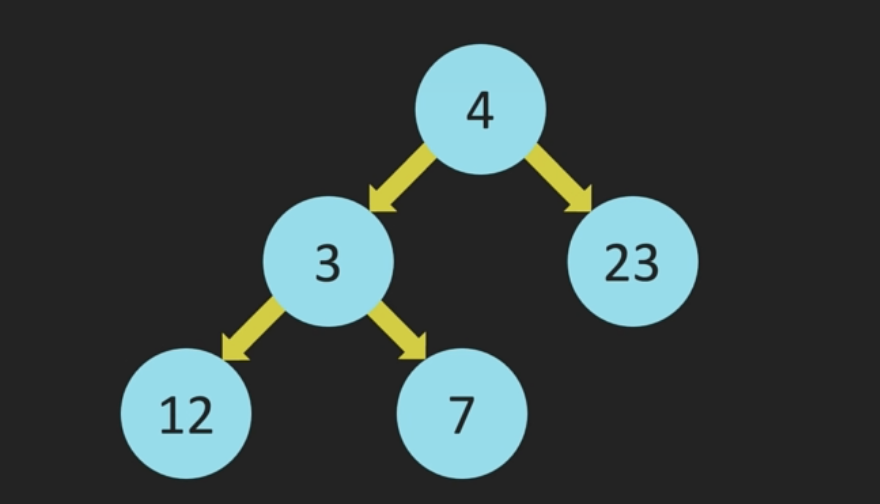
    2. 완전 이진 트리(complete binary tree): 부모, 왼쪽 자식, 오른쪽 자식 순으로 채워지는 트리를 말한다. 마지막 레벨 노드를 제외하고 모든 노드가 가득 차 있어야 하며, 마지막 레벨 노드도 왼쪽으로 몰려 있어햐 한다.
       
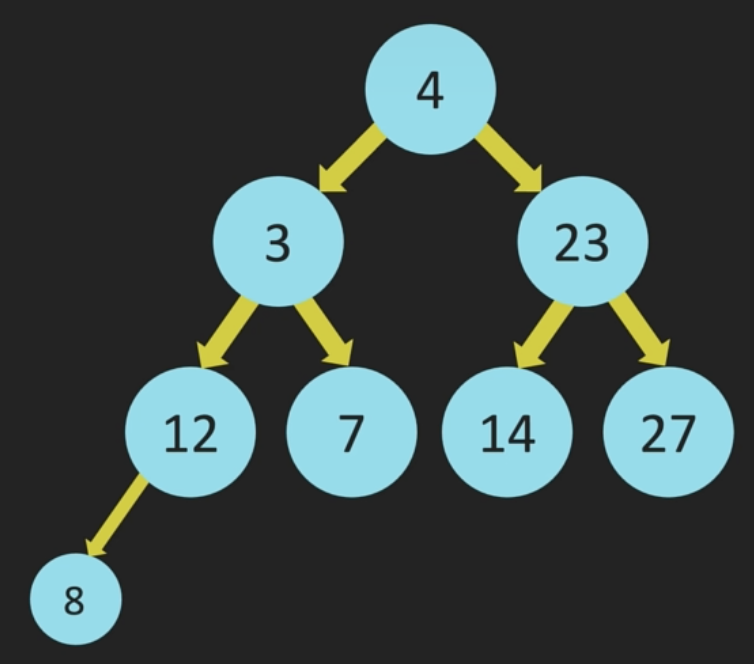
    3. 포화 이진 트리(perfect binary tree): 모든 리프 노드의 레벨이 동일하고 모든 레벨이 가득 채워져 있는 이진 트리를 의미한다. 즉, 모든 내부 노드가 두 개의 자식 노드를 가진다.
       

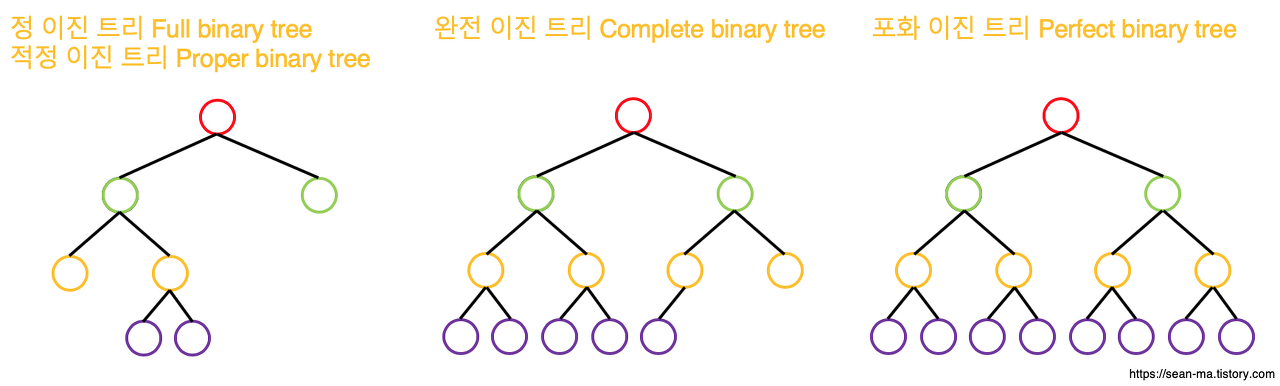
이진 검색 트리 (Binary search tree)

• 이진 탐색(binary search)과 연결 리스트(linked list)를 결합한 자료구조의 일종
• 각 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값을 가진 노드로 이루어짐
• 각 노드의 오른쪽 서브트리에는 해당 노드보다 큰 값을 가진 노드로 이루어짐
• 서브트리 또한 이진 탐색 트리로 이루어져 있음

Implement

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BST {
  constructor() {
    this.root = null;
  }

  insert(value) {
    const newNode = new Node(value);
    if (!this.root) {
      this.root = newNode;
      return this;
    }

    let temp = this.root;
    while (true) {
      if (temp.value === newNode.value) return undefined;
      if (newNode.value < temp.value) {
        if (temp.left === null) {
          temp.left = newNode;
          return this;
        }
        temp = temp.left;
      } else {
        if (temp.value === null) {
          temp.right = newNode;
          return this;
        }
        temp = temp.right;
      }
    }
  }

  contain(value) {
    if (this.root === null) return false;
    let temp = this.root;
    while (temp) {
      if (value < temp.value) {
        temp = temp.left;
      } else if (value > temp.value) {
        temp = temp.right;
      } else {
        return true;
      }
    }
    return false;
  }
}