Tree
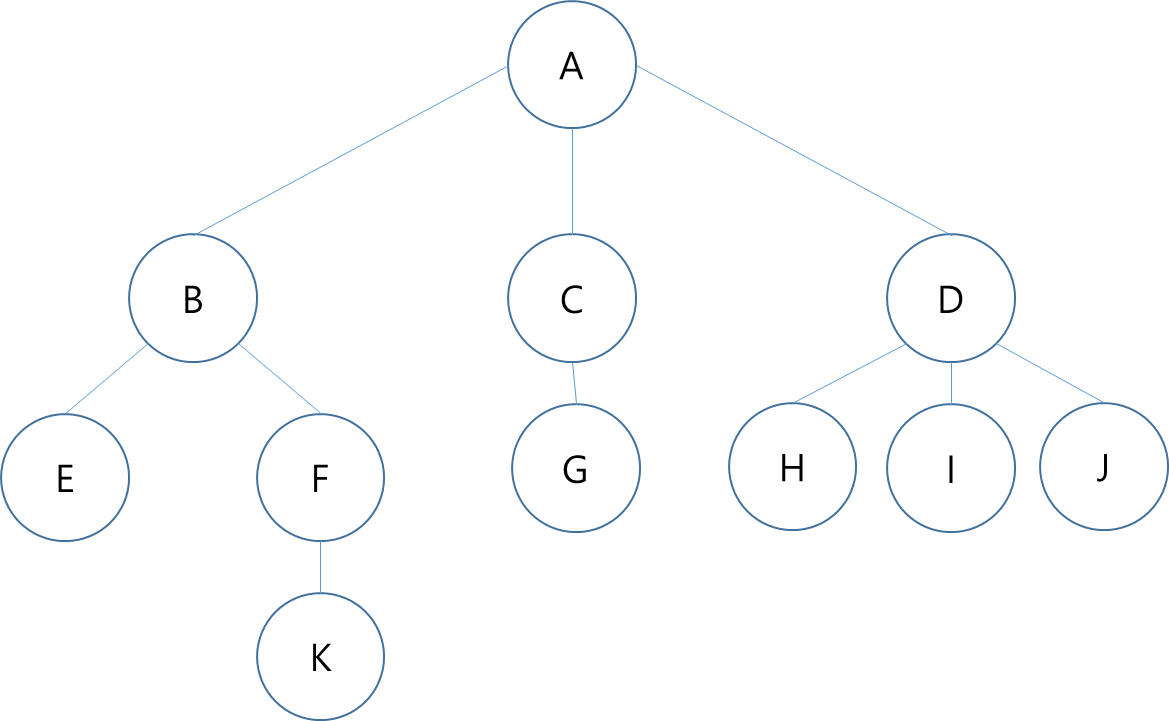
Tree의 개념
- 비선형 구조
- 원소들 간에 1:n 관계를 가지는 자료구조
- 원소들 간에 계층관계를 가지는 계층형 자료구조
- 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조
Tree의 용어 정리
- 노드 중 최상위 노드를 루트라 한다.
- 루트의 부 트리를(subtree)라 한다.
- 노드(node) - 트리의 원소
- 간선(edge) - 노드를 연결하는 선, 부모 노드와 자식 노드를 연결
- Root - 트리의 시작 노드
- sibling node(형제 드) - 같은 부모 노드의 자식 노드들
- subtree(서브 트리) - 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
- 조상 노드 - 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
- 자손 노드 - 서브 트리에 있는 하위 레벨의 노드들
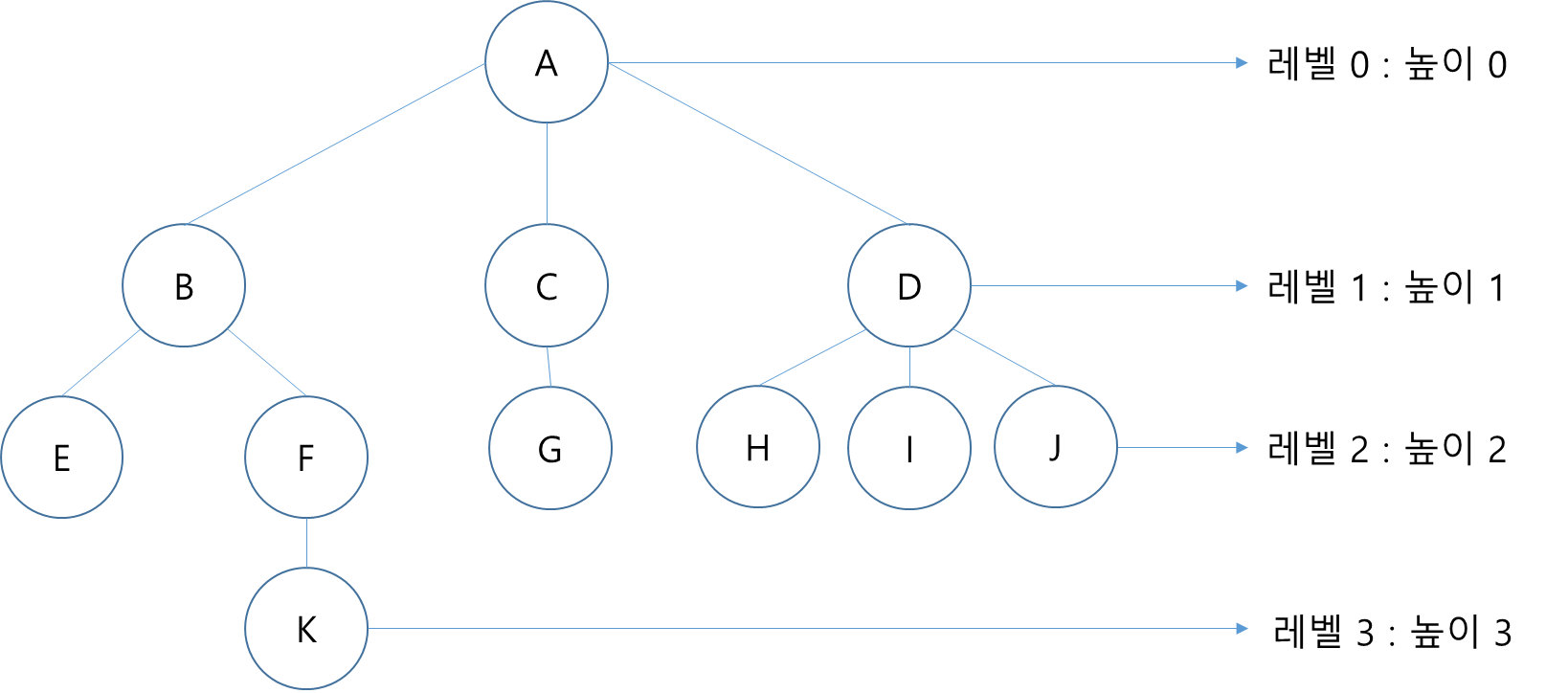
차수(degree)
- 노드의 차수 : 노드에 연결된 자식 노드의 수
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
- 단말 노드(리프 노드) : 차수가 0인 노드, 자식 노드가 없는 노드
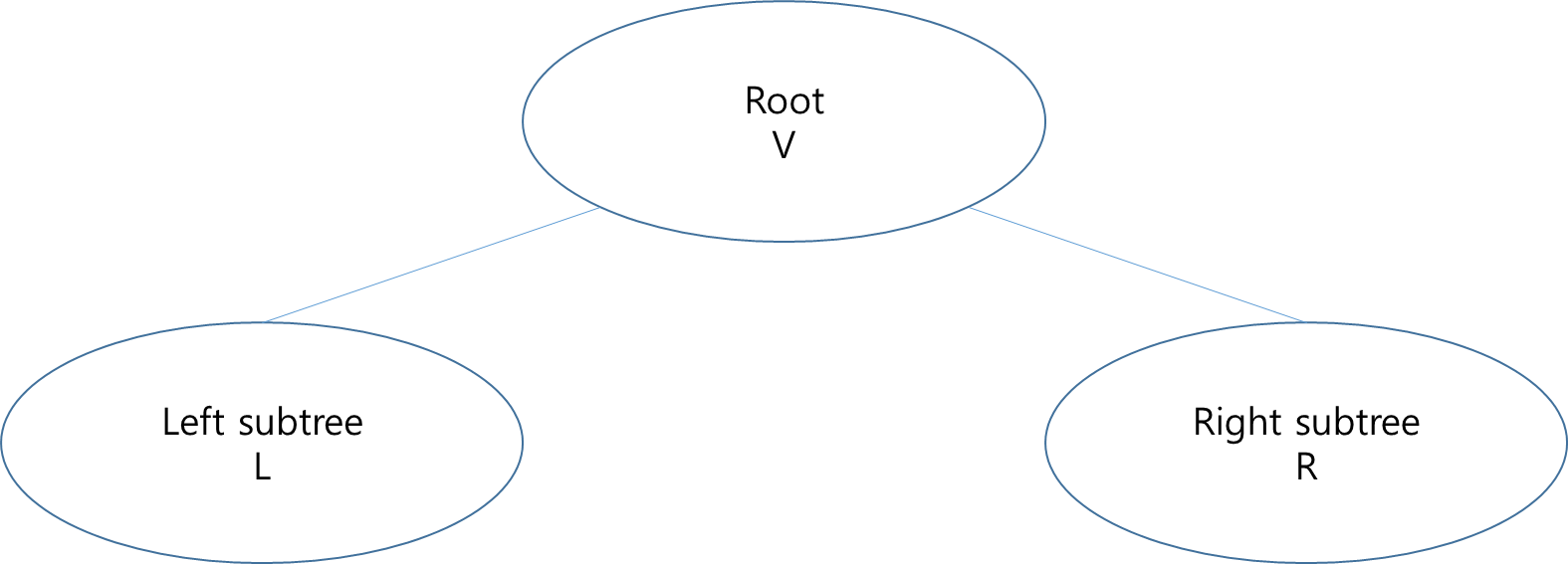
이진 트리
- 모든 노드들이 2개의 서브트리를 갖는 특별한 형태의 트리
- 각 노드가 자식 노드를 최대한 2개까지만 가질 수 있는 트리
- Level i 에서 노드의 초대 개수는 2^i 개
- 왼쪽 자식 노드(left child node)
- 오른쪽 자식 노드(right child node)
포화 이진 트리
- 모든 레벨에 노드가 포화상태로 차 있는 이진 트리
- 높이가 h일 때, 최대의 노드 개수인 (2^(h+1)-1)의 노드를 가진 이진트리
- 높이 3 : 2^(3+1) - 1 -> 15개의 노드
완전 이진 트리
- 높이가 h이고 노드 수가 n개 일 때, 포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리
편향 이진 트리
- 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 이진트리
순회
- 트리의 각 노드를 중복되지 않게 전부 방문하는 것을 말하는데 트리는 비 선형 구조이기 때문에 선형구조에서와 같이 선후 연결 관계를 알 수 없다.
- 3가지 순회
| 전위순회(preorder tracersal) | 중위 순회(inorder traversal) | 후위 순회(postorer traversal) |
|---|
| VLR | LVR | LRV |
| 부모 노드 방문 후, 자식 노드를 자,우 순서로 방문 | 왼쪽 자식 노드, 부모 노드, 오른쪽 자식 노드 순서로 방문 | 자식 노드를 좌우 순서로 방문한 후, 부모노드로 방문한다. |
전위 순회
def preorder_traverse(T) :
if T:
visit(T)
preorder_traverse(T.left)
preorder_traverse(T.right)
중위 순회
def inorder_traverse(T) :
if T :
inorder_traverse(T.left)
visit(T)
inorder_traverse(T.right)
후위 순회
def postorder_traverse(T) :
if T:
postorder_traverse(T.left)
postorder_traverse(T.right)
visit(T)
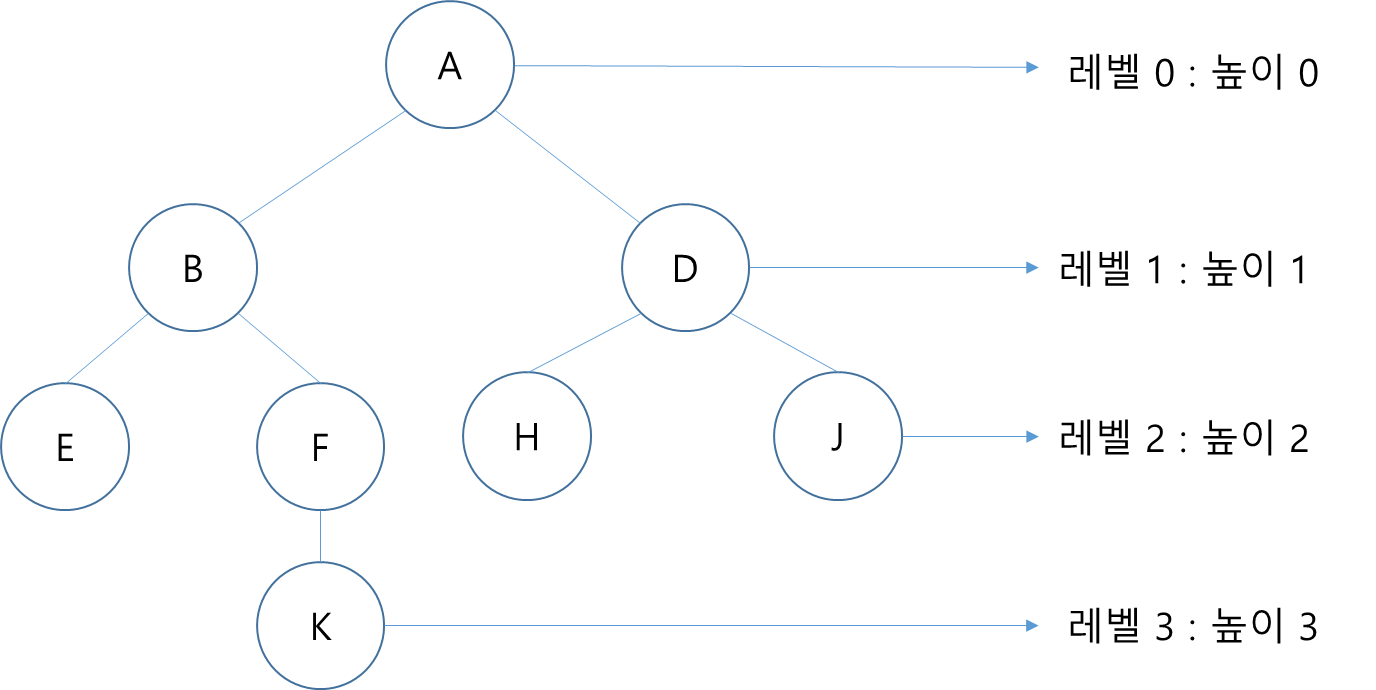
Example
- 전위 순회(preorder traversal) : A B E F K D H J
- 중위 순회(inorder traversal) : E B K F A H D J
- 후위 순회(postorder traversal) : E K F B H J D A
이진트리의 표현
- 배열을 이용한 이진 트리의 표현
- 루트의 번호를 1로 함
- 레벨 n에 있는 노드에 대하여 왼쪽부터 오른쪽으로 2^n부터 2^(n+1) - 1 까지 번호를 차례로 부여
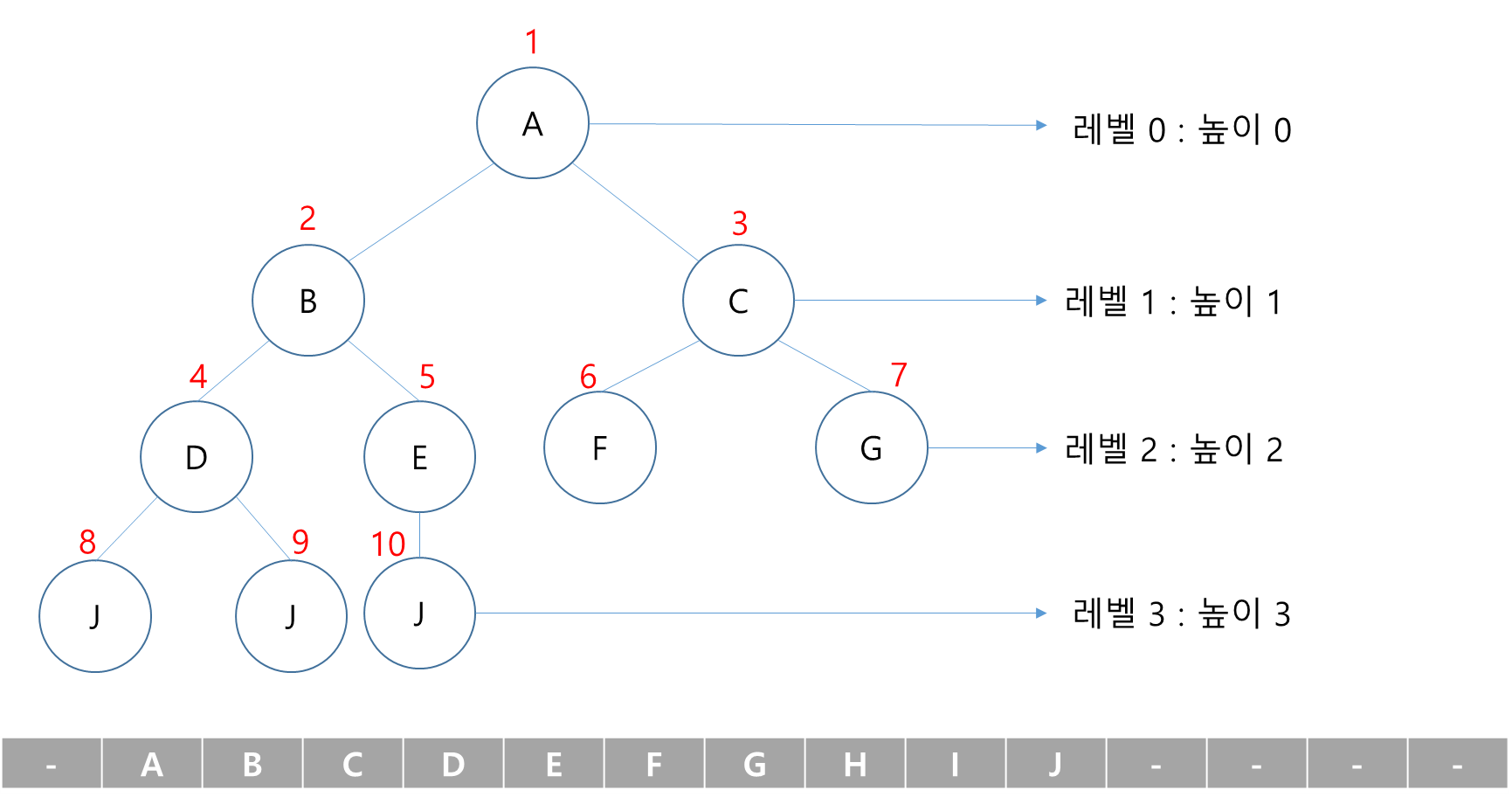
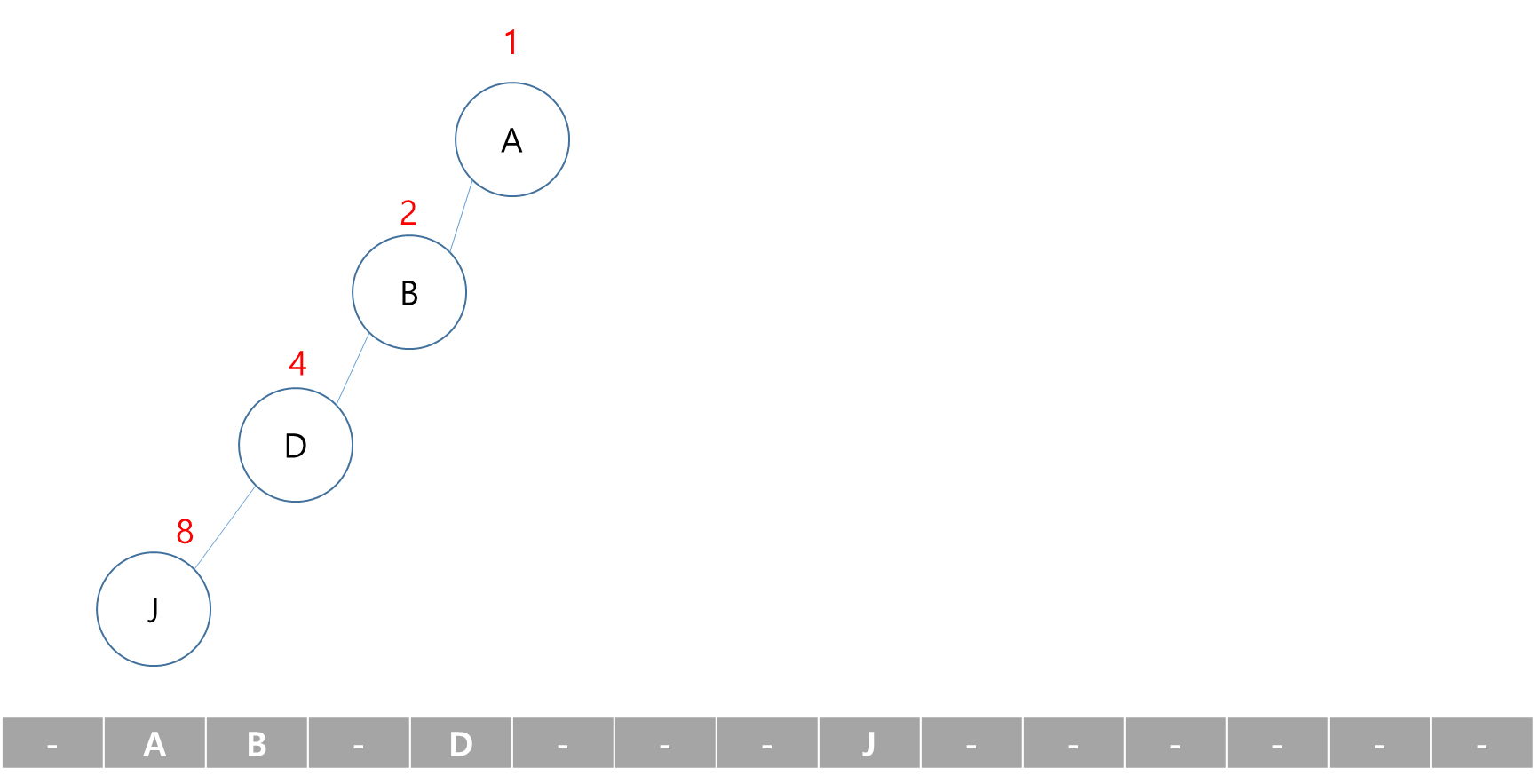
배열을 이용한 이진 트리 표현의 단점
- 편향 이진 트리의 경우에 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
- 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경 어려워 비효율적
단점 해소를 위한 연결리스트
- 배열을 이용한 이진 트리의 표현의 단점을 보완하기 위해 연결리스트를 이용하여 트리를 표현할 수 있다.
- 이진트리의 표현
- 이진 트리의 모든 노드는 최대 2개의 자식 노드를 가지므로 일정한 구조의 단순 연결리시트 노드를 사용하여 구현
수식트리
- 수식을 표현하는 이진 트리
- 수식 이진 트리라고 부르기도 함
- 연산자는 루트 노드이거나 가지 노드
- 피연산자는 모두 잎 노드