학습한 내용
실습 1 - pytorch를 사용해 인공신경망 구현(0602 내용)
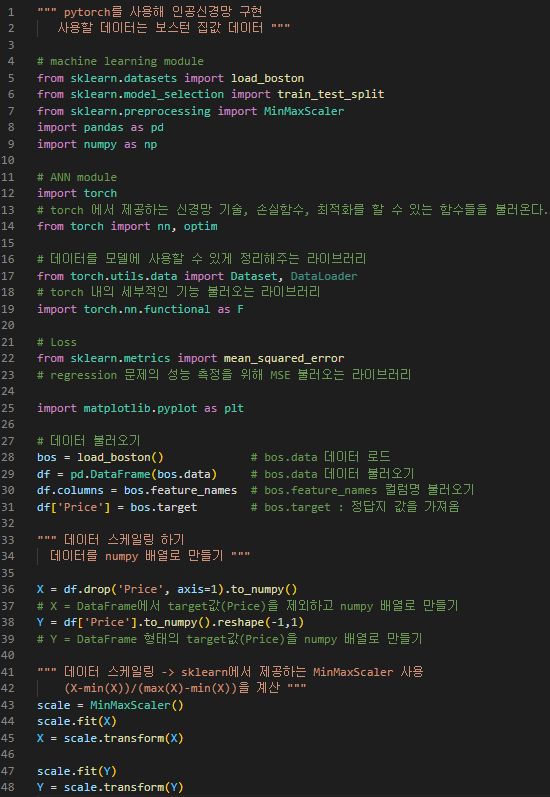
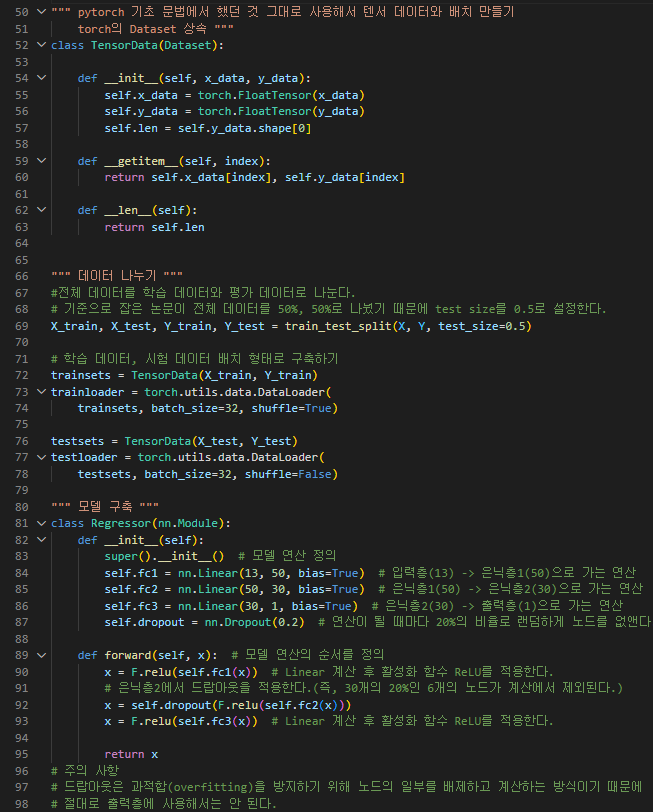
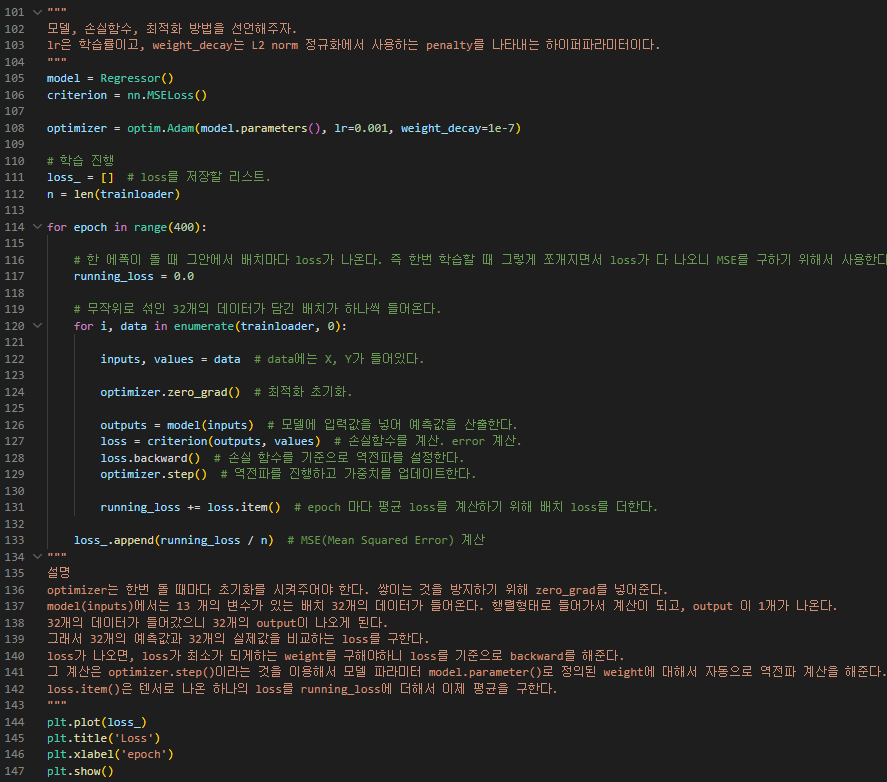
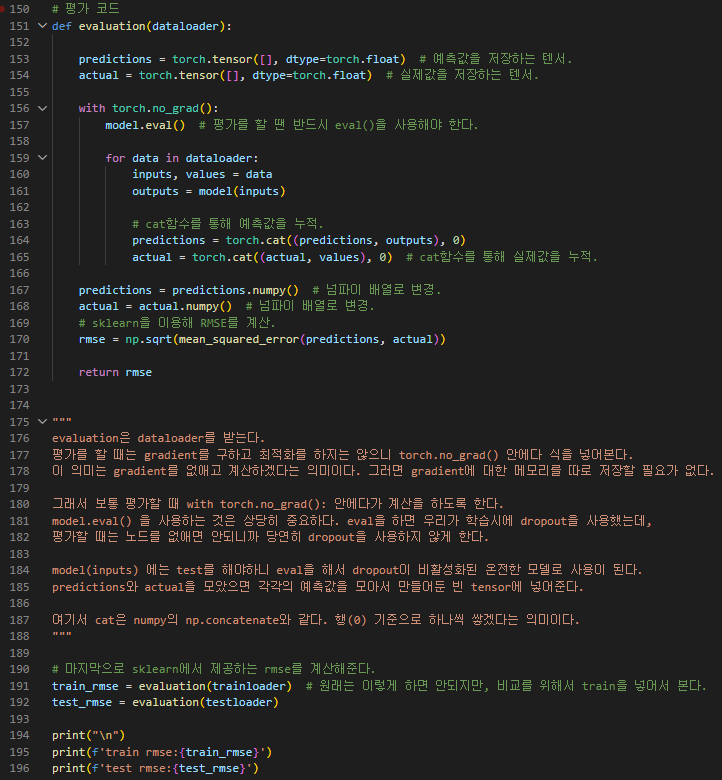
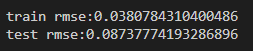
결과 >> 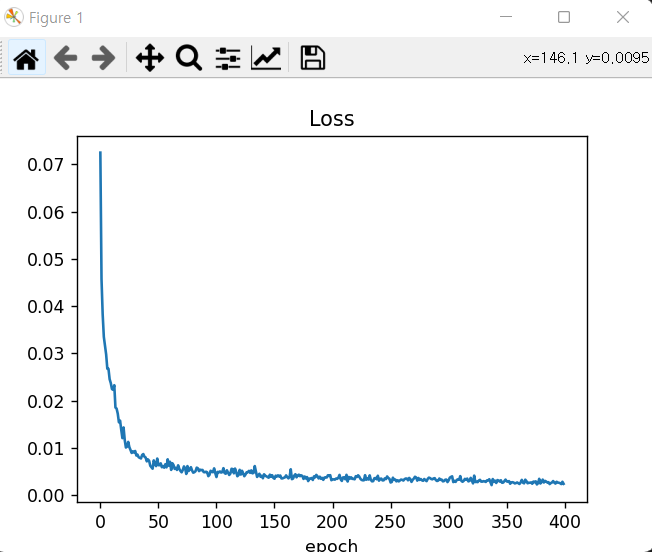
인공 지능 신경망 개념
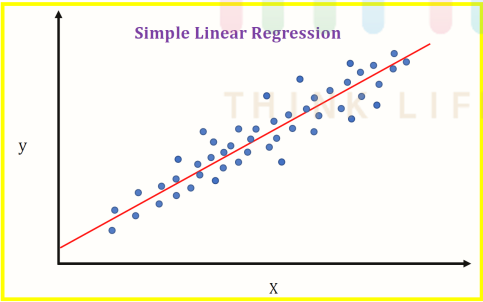
1. 선형 회귀(Linear Regression)
- 실제 데이터를 바탕으로 모델을 생성해서 만약 다른 값을 넣었을 때 발생할 출력값을 예측하는데 있다.
- 선형 회귀 발생하는 오차, 손실: MSE(평균 제곱 오차)을 이용해서 계산
- 목표: 모든 데이터로부터 나타나는 오차 평균을 최소화할 수 있는 최적의 기울기와 절편을 찾는 것
-> 파라미터를 임의로 정한 다음에 조금씩 변화시켜가며 손실을 점점 줄여가는 방법으로 최적의 파라미터를 찾아감 : 경사하강법(Gradient Descent) - 수렴: 선형 회귀 분석을 수행하면서 파라미터를 계속 조정 하다보면 어느정도 최적의 값으로 수렴(converge)한다
- 학습률(Learning Rate): 학습률을 크게 설정하면 최적의 값을 제대로 찾지 못한다. 그렇다고 학습률을 작게 설정하면 최적의 값으로 수렴할 때까지 시간이 오래 걸리기 때문에 효율적으로 파라미터를 조정하면서도 결국 최적의 값을 찾아한다
2. 다중 선형 회귀(Multiple Linear Regression)
- 여러 개의 특성을 이용해 종속변수를 예측하기 때문에 일반 선형회귀보다 더 좋은 성능을 기대할 수 있다.
3. 이진 분류(Logistic Regression)
- 입력값에 따라 모델이 분류한 카테고리가 두 가지인 분류 알고리즘.
- 주로 어떤 대상에 대한 규칙이 True인지 False인지를 분류하는데 쓰임.
- 시그모이드 함수(Sigmoid function)

- 손실함수: 이진교차 엔트로피(Binary Cross-Entropy)사용
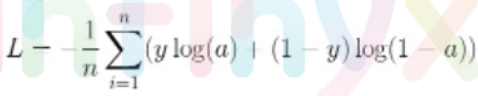
-> a는 활성화 함수를 통과한 값, y값은 0 또는 1임.
-> i번째 데이터에 대한 손실값은 :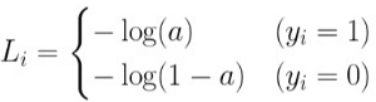
아래의 그래프는 각각 -log(a)의 그래프와 -log(1-a)의 그래프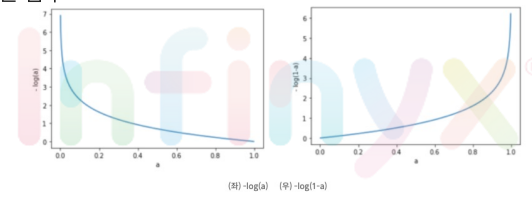
-> 손실 함수의 값을 최소화하는 과정에서 타깃이 참(True)이라면 -log(a)의 값이 작아져 a값이 1에 가까워지고, 타깃이 거짓(False)이라면 -log(1-a)의 값이 작아져 a값이 0에 가까워짐.
회귀 종류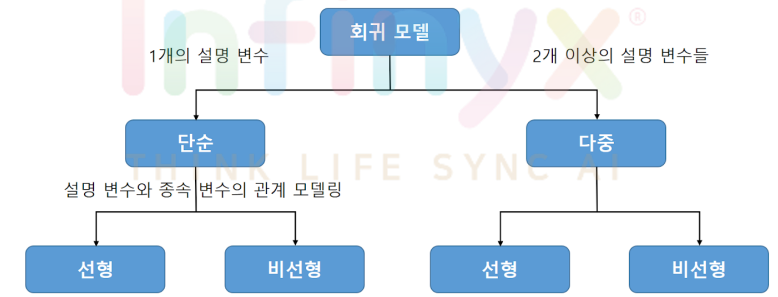
Pytorch에서 제공하는 오차 함수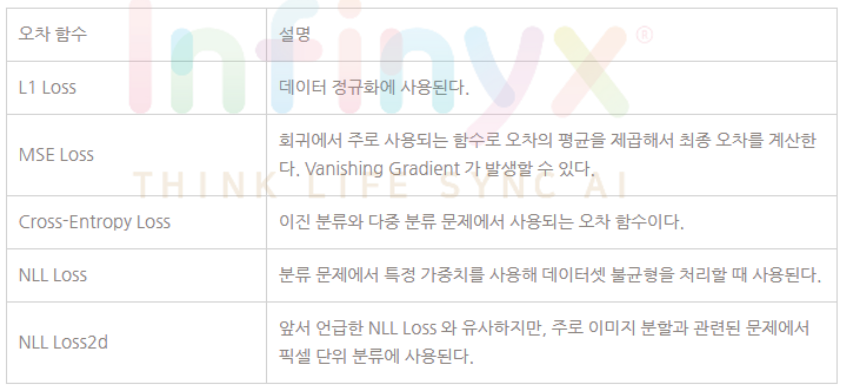
실습 2 - 선형회귀 Pytorch 구현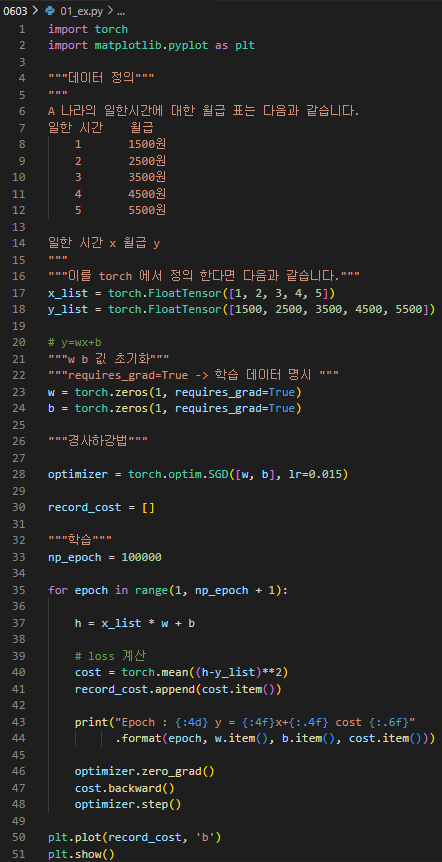
결과 >>
실습 3 - 다중 선형회귀 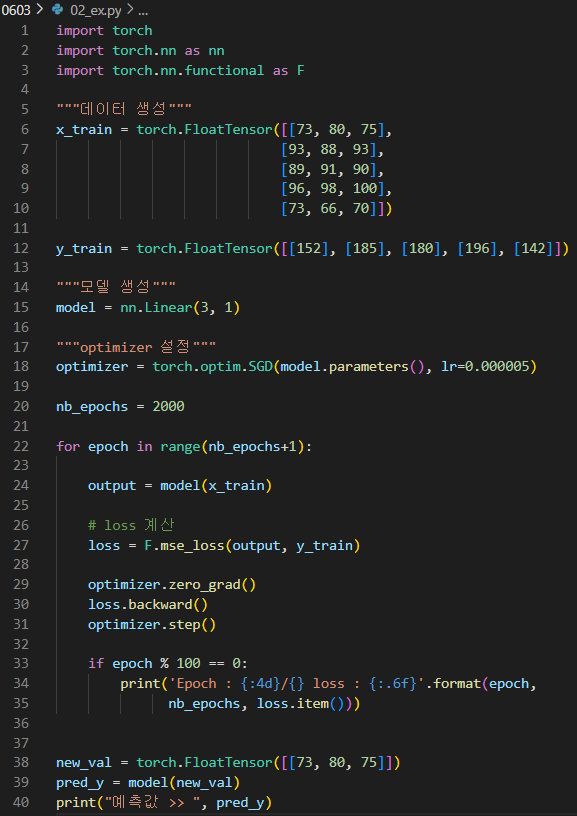
결과 >>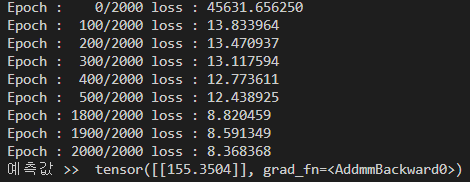
학습한 내용 중 어려웠던 점 또는 해결못한 것들
딱히 없었다.
해결방법 작성
학습 소감
오늘 강의도 딱히 어려운 것은 없었다. 최근 기술 동향 사이트들도 살펴봐야겠다.