학습한 내용
딥러닝 학습 방법
모델 선택 & 학습: 기존 모델 사용 시
- 일반적으로 ImageNet 기준 상 성능이 좋았던 모델 사용
- 학습할 데이터셋의 크기 등을 고려하여 적절한 모델을 선택하며, 학습 환경에 맞춰
모델을 세부 조정하는 과정에서 새로운 모델을 개발하기도 함 - ResNet 50, VggNet 16 등 모델 사용
성능 측면 – 무거운 딥 러닝 모델
1) VGG-16 (파라미터는 많으나, 생각보다 빠르고 성능이 좋음)
2) ResNet50-SE (ResNet101이나 ResNet152 대비 efficient, GPU 서빙의 마지노선)
3) ResNeXT101-SE + FPN (FPN은 detection등에 적용할 때 성능에 큰 영향)
4) Xception 계통 (의외로 효율적이고 강력한 모델, group-conv 기반)
5) EfficientNet-B4 (효율적이고 성능이 좋지만, dw-conv 기반)
속도 측면 – 가벼운 딥 러닝 모델
1) ResNet-18 (ResNet-50보다 빠르지만, 여전히 크기가 큼)
2) Xception 계통 (CPU용, Xception을 작게 만들어 사용)
3) MobileNetV1 (CPU용, MobileNetV2보다 더 좋을 때가 많음)
4) YOLO 계열
5) SSD 계열
딥러닝 성과 지표
회귀 모델의 성능 지표
- 회귀모델이 잘 만들어 졌는지 확인하는 성능평가지표는 실제값과 예측값
을 오차들의 통계값을 활용합니다.
1. 평균 절대 오차(MAE)
실제 정답 값과 예측 값의 차이를 절댓값으로 변환한 뒤 합산하여 평균을 구한다. 특이값이 많은 경우에 주로 사용되고 값이 낮을수록 좋다.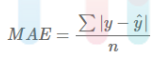
장점
• 직관점임
• 정답 및 예측 값과 같은 단위를 가짐
단점
• 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘듦
• 스케일 의존적임(scal dependency): 모델마다 에러율 크기가 동일해도 에러율은 동일하지 않음
2. 평균 제곱 오차(MSE)
실제 정답 값과 예측 값의 차이를 제곱한 뒤 평균을 구한다. 값이 낮을수록 좋다.
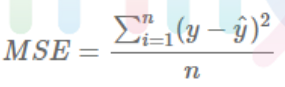
장점
• 직관적임
단점
• 제곱하기 때문에 1미만의 에러는 작아지고, 그 이상의 에러는 커짐
• 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘듦
• 스케일 의존적임(scal dependency): 모델마다 에러율 크기가 동일해도 에러율은 동일하지 않음
3. 평균 제곱근 오차(RMSE)
MSE에 루트는 씌워서 에러를 제곱해서 생기는 값의 왜곡이 줄어든다. 값이 낮을수록 좋다.
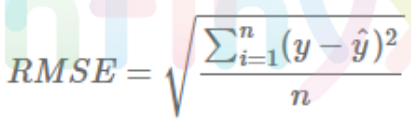
장점
• 직관적임
단점
• 제곱하기 때문에 1미만의 에러는 작아지고, 그 이상의 에러는 커짐
• 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘듦
• 스케일 의존적임(scal dependency): 모델마다 에류 크기가 동일해도 에러율은 동일하지 않음
4. 평균 절대 비율 오차(MAPE)
MAE를 비율, 퍼센트로 표현하여 스케일 의존적 에러의 문제점을 개선한다 값이 낮을수록 좋다.
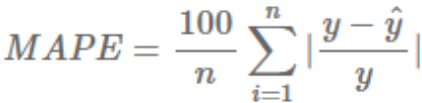
장점
• 직관적임
• 다른 모델과 에러율 비교가 쉬움
단점
• 실제 정답보다 낮게 예측했는지, 높게 했는지를 파악하기 힘듦
• 실제 정답이 1보다작을 경우,무한대의 값으로 수렴할 수 있음
분류 모델의 성능 평가 지표
- 분류 모델(classifier)을 평가할 때 주로 Confusion Matrix를 기반으로 Accuracy, Precision, Recall, F1 score를 측정한다.
Confusion Matrix(혼동 행렬, 오차 행렬)
- 분류 모델(classifier)의 성능을 측정하는 데 자주 사용되는 표로 모델이 두 개의 클래스를 얼마나 헷갈려하는지 알 수 있다.
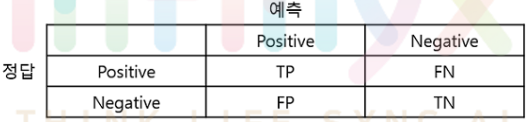
• T(True): 예측한 것이 정답
• F(False): 예측한 것이 오답
• P(Positive): 모델이 positive라고 예측
• N(Negative): 모델이 negative라고 예측
• TP(True Positive): 모델이 positive라고 예측했는데 실제로 정답이 positive (정답)
• TN(True Negative): 모델이 negative라고 예측했는데 실제로 정답이 negative (정답)
• FP(False Positive): 모델이 positive라고 예측했는데 실제로 정답이 negative (오답)
• FN(False Negative): 모델이 negative라고 예측했는데 실제로 정답이 positive (오답)
1. Accuracy(정확도)
- 모델이 전체 문제 중에서 정답을 맞춘 비율이다.
- 데이터가 불균형할 때(ex) positive:negative=9:1)는 Accuracy만으로 제대로 분류했는지는 알 수 없기 때문에 Recall과 Precision을 사용한다.
- 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋다.
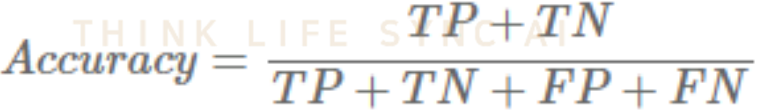
2. Precision(정밀도) = PPV(Positive Predictive Value)
- 모델이 positive라고 예측한 것들 중에서 실제로 정답이 positive인 비율이다.
- 실제 정답이 negative인 데이터를 positive라고 잘못 예측하면 안 되는 경우에 중요한 지표가 될 수 있다.
- Precision을 높이기 위해선 FP(모델이 positive라고 예측했는데 정답은 negative인 경우)를 낮추는 것이 중요하다.
- 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋다.
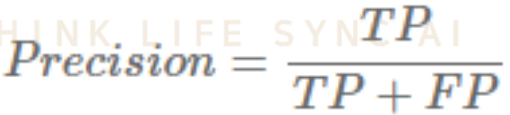
3. Recall(재현율) = Sensitivity(민감도) = TPR(True Positive Rate)
- 실제로 정답이 positive인 것들 중에서 모델이 positive라고 예측한 비율이다.
- 실제 정답이 positive인 데이터를 negative라고 잘못 예측하면 안 되는 경우에 중요한 지표가 될 수 있다.
- Recall를 높이기 위해선 FN(모델이 negative라고 예측했는데 정답이 positive인 경우)을 낮추는 것이 중요하다.
- 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋다.

4. F1 score
- Recall과 Precision의 조화평균이다.
- Recall과 Precision은 상호 보완적인 평가 지표이기 때문에 F1 score를 사용한다.
- Precision과 Recall이 한쪽으로 치우쳐지지 않고 모두 클 때 큰 값을 가진다.
- 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋다.
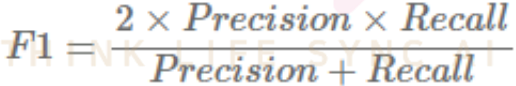
객체 인식 모델의 성능 지표
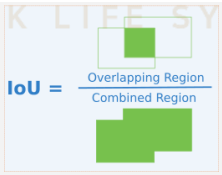
1. IOU
- 객체 검출의 정확도를 평가하는 지표. 일반적으로 Object Detection에서 개별 객체(Object)에 대한 검출(Detectino)이 성공하였는지를 결정하는 지표.
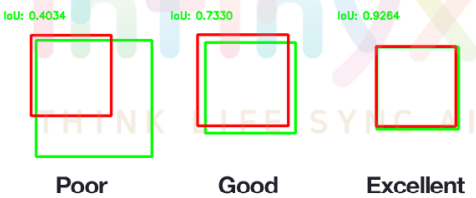
- 0~1 사이의 값을 가지며, 1에 가까울수록 좋다.
- 실제 객체 위치 bounding box B_gt=ground truth와 예측한 bounding box B_p=prediction 두 box가 중복되는 영역의 크기를 통해 평가하는 방식으로 겹치는 영역이 넓을수록 잘 예측한 것으로 평가함.
2. Precision Recall Curve
- P-R 곡선(Precision-Recall Curve)는 confidence score를 조정하면서 얻은 Recall 값의 변화에 따른 Precision을 나타낸 곡선으로 모델(Object detector)의 성능을 평가하는 방법으로, 일반적으로 P-R 곡선의 면적(AOU, Area under curve) 값으로 계산됨
- Recall이 높아져도 precision이 유지되는 경우, 특정 Class 검출을 위한 모델 성능이 좋을것으로 평가됨. 즉 Confidence threshold를 변경하더라도, Precision과 Recall이 모두 높은 경우 모델 성능이 좋을 것으로 평가
- 관련된 객체만 detection 할 수 있는 모델. 즉 오탐 낮은(0 FP = Precision 높음) 경우도 좋은 모델로 평가할 수 있음
- 실제 Object를 모두 찾아내기 위해 Object 수를 많이 Detect 하는 경우(FP 높은 경우 = Precision이 낮음), 일반적으로 P-R 곡선이 높은 Precision으로 시작하지만, Recall이 증가함에 따라 감소함
3. AP
- AP 곡선(Average Precison curve)은 Precision과 Recall을 고려한 종합적 평가 지표이며, 실제로 AP는 0~1 사이의 모든 Recall에 대응하는 평균 Precision
- 다른 검출방식에 비해 곡선의 업다운이 심하고, 곡선이 자주 교차하는 경향이 있기 때문에 같은 플롯으로 비교하는 것이 쉽지 않음. AP 평가 지표는 다양한 모델을 비교하는데에 유용한 방식
- 2010년부터, PASCAL VOC 챌린지에서 AP 계산 방식이 변경되어, 현재는 11점 보간법(11-point interpolation)뿐만 아니라 모든 점 보간법(interpolating all data)을 사용함
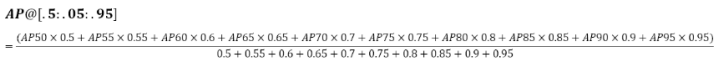
4. mAP(mean Average Performance)
- 모든 점 보간법을 이용해서 AP를 구한 값의 평균
- 여러 Class에 대한 AP를 구해야 하므로, 각각의 Class에 대해 AP를 구하고 평균을 산출

학습한 내용 중 어려웠던 점 또는 해결못한 것들
없다.
해결방법 작성
학습 소감
이론적인 부분이라 쉬웠다.