Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

20. 분할 정복

재귀를 응용하는 알고리즘, 분할 정복을 익혀 봅시다.

Java / Python

7. 행렬 제곱

10830번

분할 정복으로 행렬의 거듭제곱을 빠르게 계산하는 문제

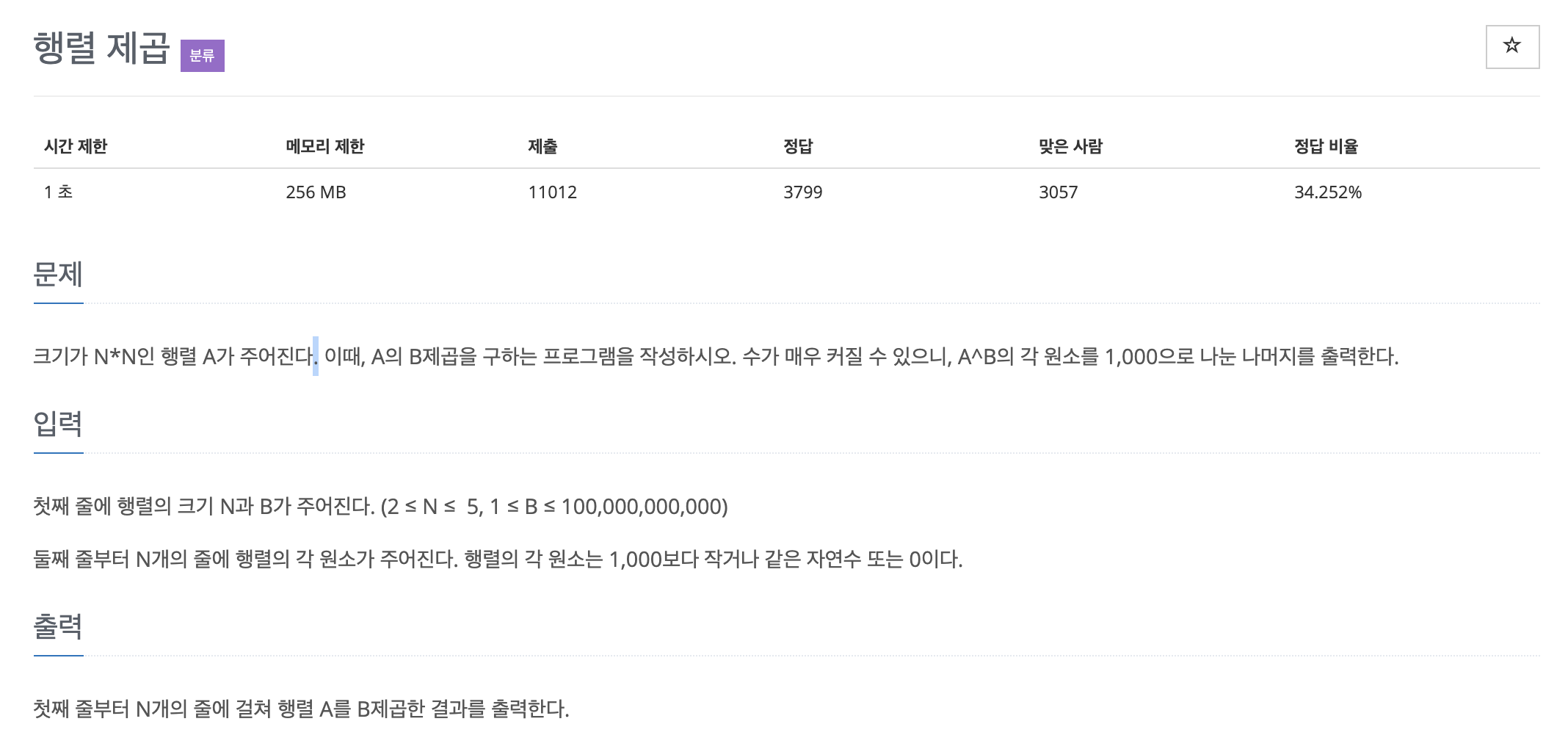
이번 문제는 크기가 NxN인 행렬 A가 주어지는데, 이때, A의 B제곱을 구하는 프로그램을 작성하는 문제입니다.

• Java

import java.util.Scanner;

public class Main {
	static int N;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		long b = sc.nextLong();
		long[][] data = new long[N][N];
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				data[i][j] = sc.nextLong();
			}
		}
		long[][] result = pow(data, b);
		printData(result);
	}

	static long[][] pow(long[][] data, long b) {

		if (b == 0) {
			long[][] tmp = new long[N][N];
			for (int i = 0; i < N; i++) {
				for (int j = 0; j < N; j++) {
					tmp[i][j] = 1;
				}
			}
			return tmp;
		}
		if (b == 1)
			return data;
		if (b % 2 == 1) {	//홀수
			long[][] tmp = pow(data, b - 1);
			return countPow(data, tmp);
		} else {//짝수
			long[][] tmp = pow(data, b / 2);
			return countPow(tmp, tmp);
		}
	}

	static long[][] countPow(long[][] dataA, long[][] dataB) {
		long[][] result = new long[N][N];
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				long tmp = 0;
				for (int k = 0; k < N; k++) {
					tmp += dataA[i][k] * dataB[k][j];
				}
				result[i][j] = tmp % 1000;
			}
		}
		return result;
	}

	static void printData(long[][] result) {
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				System.out.print((result[i][j]%1000)  + " ");
			}
			System.out.println("");
		}
	}
}

• Python

import sys

N, b = map(int, sys.stdin.readline().split())
MOD = 1000
matrix = [list(map(lambda x: x % MOD, map(int, sys.stdin.readline().split()))) for _ in range(N)]

def power(m, y):
    if y == 1:
        return m
    partial = power(m, y // 2)
    partial_square = multi(partial, partial)
    if y % 2 == 0:
        return partial_square
    elif y % 2 == 1:
        return multi(partial_square, m)


def multi(matrix_1, matrix_2):
    length = len(matrix_1)
    result = [[0 for _ in range(length)] for _ in range(length)]
    for i in range(length):
        for j in range(length):
            result[i][j] = sum([(matrix_1[i][k] * matrix_2[k][j])%MOD for k in range(length)])%MOD
    return result

answer = power(matrix, b)
for i in range(N):
    print(' '.join(map(str, answer[i])))