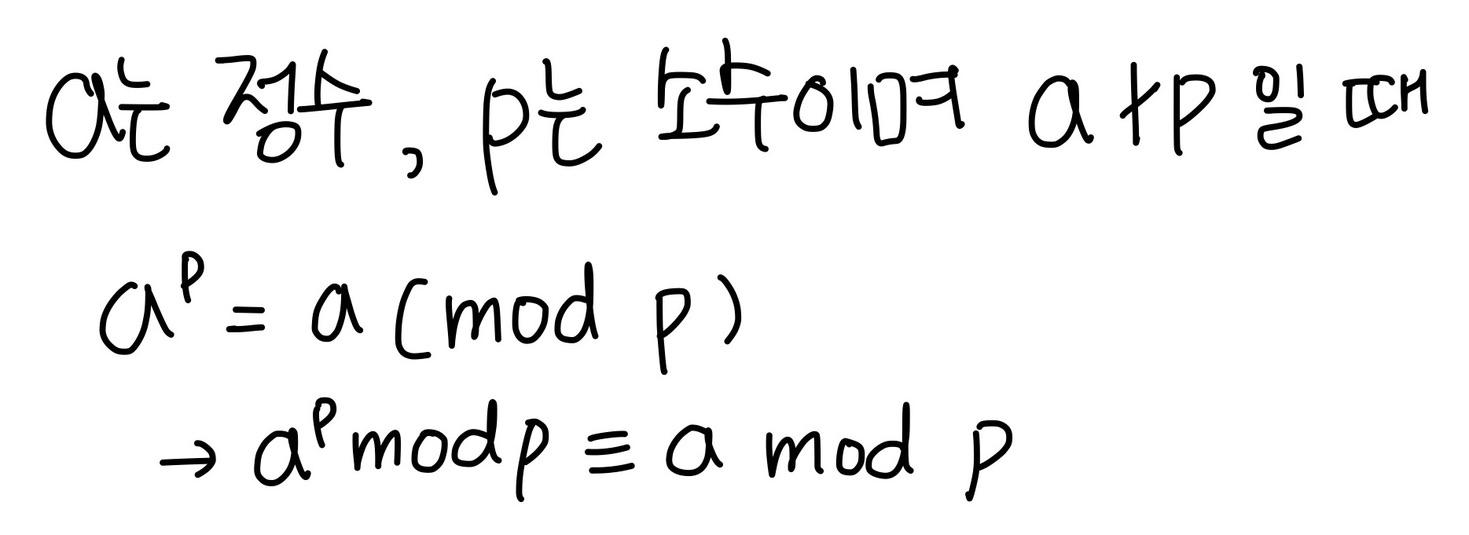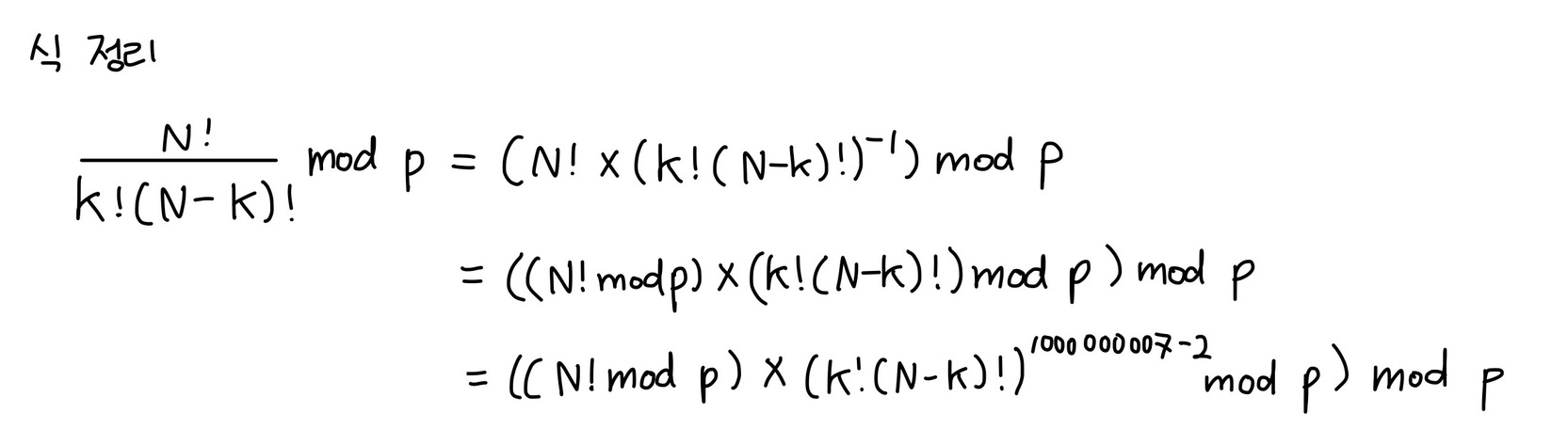Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

20. 분할 정복

재귀를 응용하는 알고리즘, 분할 정복을 익혀 봅시다.

Java / Python

5. 이항 계수 3

11401번

분할 정복을 사용한 거듭제곱과 페르마의 소정리를 이용해 곱셈의 역원을 구하는 문제

이번 문제는 자연수 N과 정수 K가 주어졌을 때 이항 계수를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하는 문제입니다.
분할 정복과 페르마의 소정리를 이용합니다.
페르마의 소정리의 정의는 다음과 같습니다.


위와 같은 방식으로 구현가능합니다.

• Java

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
 
public class Main {
 
	final static long P = 1000000007;
	public static void main(String[] args) throws IOException {
 
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
		
		long N = Long.parseLong(st.nextToken());
		long K = Long.parseLong(st.nextToken());
		
		// 분자 N!
		long numer = factorial(N);
		
		// 분모 (K! * (N-K)!) mod p
		long denom = factorial(K) * factorial(N - K) % P;	
	
		
		// N! * 분모의 역((K! * (N-K)!) 
		System.out.println(numer * pow(denom, P - 2) % P);
		
	}	
	
	public static long factorial(long N) {
		long fac = 1L;
		
		while(N > 1) {
			fac = (fac * N) % P;
			N--;
		}
		return fac;
	}	
 
	// base : 밑 / expo : 지수
	// 거듭 제곱 <- 분할 정복 방식
	public static long pow(long base, long expo) {
		if(expo == 1) {
			return base % P;
		}
		
		long temp = pow(base, expo / 2);
		
		if(expo % 2 == 1) {
			return (temp * temp % P) * base % P;
		}
		return temp * temp % P;
		
	}
}

• Python

import sys 
N, K = map(int, sys.stdin.readline().split()) 
mod = 1000000007

def power(a, b): # 분할 정복을 이용하여 a^b
    if b == 0:
        return 1
    if b % 2:  # 홀수이면
        return (power(a, b // 2) ** 2 * a) % mod
    else:
        return (power(a, b // 2) ** 2) % mod

# nCk
fact = [1 for _ in range(N + 1)]

for i in range(2, N + 1):
    fact[i] = fact[i - 1] * i % mod

# A = nCk의 분자 / B = 분모
A = fact[N]
B = (fact[N - K] * fact[K]) % mod

# 페르마의 소정리 이용
print((A % mod) * (power(B, mod - 2) % mod) % mod)