Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

28. 트리

대표적인 그래프 종류 중 하나인 트리를 다뤄 봅시다.

Java / Python

2. 트리의 지름

1167번

BFS나 DFS로 트리에서 가장 먼 두 점을 찾는 문제

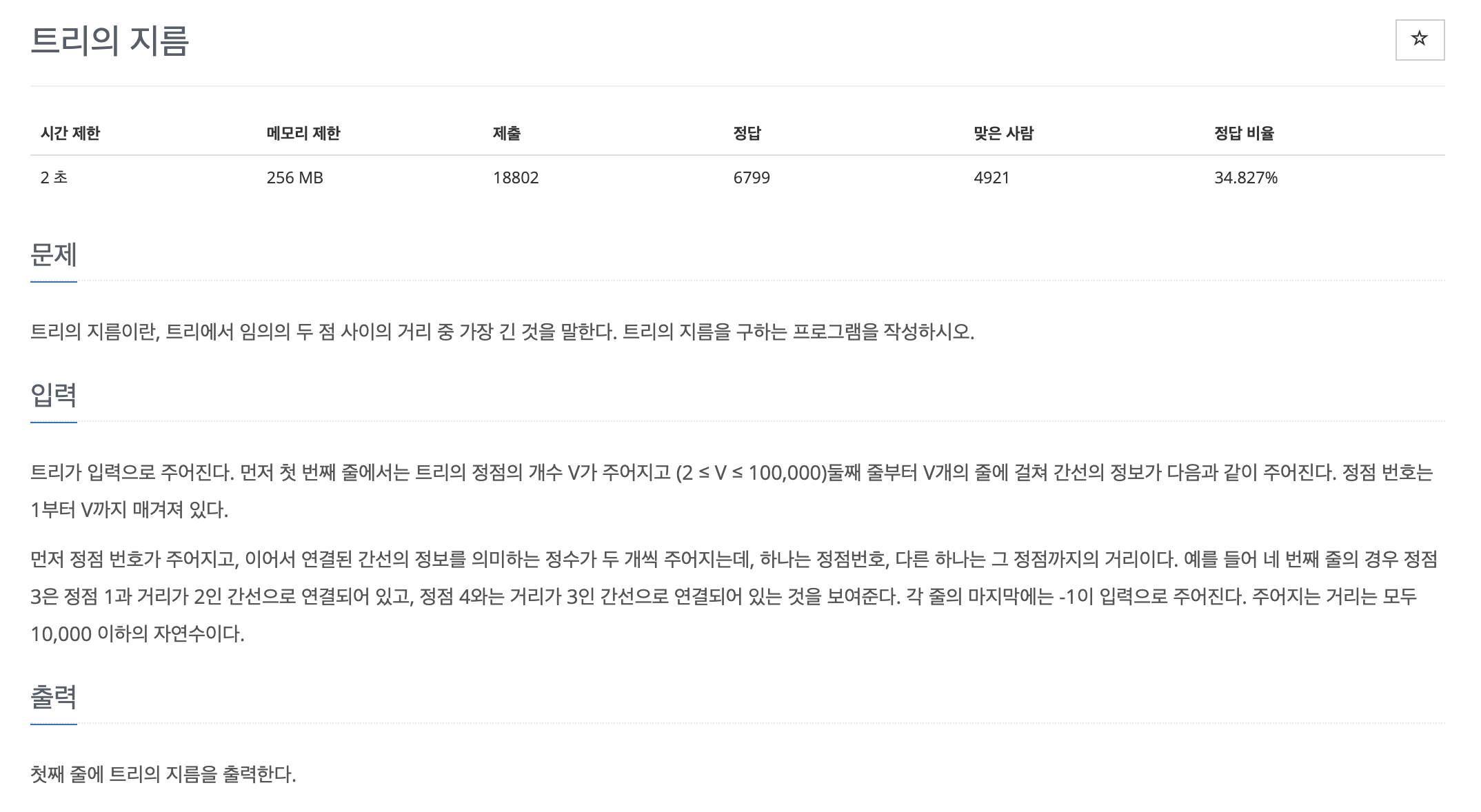
이번 문제는 트리에서 임의의 두 점 사이의 거리 중 가장 긴 부분, 즉, 트리의 지름을 구하는 프로그램을 작성하는 문제이다.
루트에서 가장 멀리 있는 노드와, 그 노드에서 가장 멀리 있는 노드와의 거리를 구하는 문제이다. class Node와 인접리스트를 이용하여 문제를 해결한다.
코드 구현
1. dfs를 통해 임의의 정점 하나에서 가장 먼 정점을 구한다.
2. dfs를 통해 구한 정점으로 부터 가장 먼 정점까지의 거리를 구한다.

• Java

import java.util.*;
import java.io.*;

public class Main {
	static class Node {
		int node, dist;

		public Node(int node, int dist) {
			this.node = node;
			this.dist = dist;
		}
	}

	static ArrayList<Node>[] list;
	static boolean[] visit;
	static int max = 0;
	static int node, V;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st;

		V = Integer.parseInt(br.readLine());

		list = new ArrayList[V + 1];
		for (int i = 1; i <= V; i++)
			list[i] = new ArrayList<>();

		for (int i = 0; i < V; i++) {
			st = new StringTokenizer(br.readLine());

			int nodenum = Integer.parseInt(st.nextToken());
			String str;
			while (!(str = st.nextToken()).equals("-1")) {
				int node = Integer.parseInt(str);
				int dist = Integer.parseInt(st.nextToken());
				list[nodenum].add(new Node(node, dist));
			}
		}

		visit = new boolean[V + 1];
		dfs(1, 0);

		visit = new boolean[V + 1];
		dfs(node, 0);

		bw.write(max + "\n");

		bw.flush();
		br.close();
		bw.close();
	}

	public static void dfs(int v, int len) {
		if (len > max) {
			max = len;
			node = v;
		}

		visit[v] = true;

		for (Node n : list[v]) {
			if (!visit[n.node]) {
				dfs(n.node, n.dist + len);
				visit[n.node] = true;
			}
		}
	}
}

• Python

import sys
input = sys.stdin.readline
V = int(input())
graph = [[] for _ in range(V+1)]
for i in range(V):
    path = list(map(int, input().split()))

    # 각 입력 Line의 정보를 받고 graph에 연결 정보 저장
    path_len = len(path)
    for i in range(1, path_len//2):
        graph[path[0]].append([path[2*i-1], path[2*i]])

# 첫 번째 DFS 결과
first_result = [0 for _ in range(V+1)]
 
def DFS(start, result):
    for e, d in graph[start]:
        if result[e] == 0:
            result[e] = result[start] + d
            DFS(e, result)

DFS(1, first_result) 
first_result[1] = 0

tmpmax = 0 # 최댓값 구하기
index = 0 # 최장경로 노드
 
for i in range(len(first_result)):
    if tmpmax < first_result[i]:
        tmpmax = first_result[i]
        index = i

# 최장경로 노드에서 다시 DFS를 통해 트리의 지름을 구함
result_final = [0 for _ in range(V+1)]
DFS(index, result_final)
result_final[index] = 0
print(max(result_final))