Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

27. 동적 계획법과 최단거리 역추적

지금까지는 최솟값, 최댓값, 최단거리만 찾았습니다. 이번에는 실제 최적해와 최단경로를 찾아 봅시다.

Java / Python

1. 1로 만들기 2

12852번

1로 만드는 최적해를 출력하는 문제

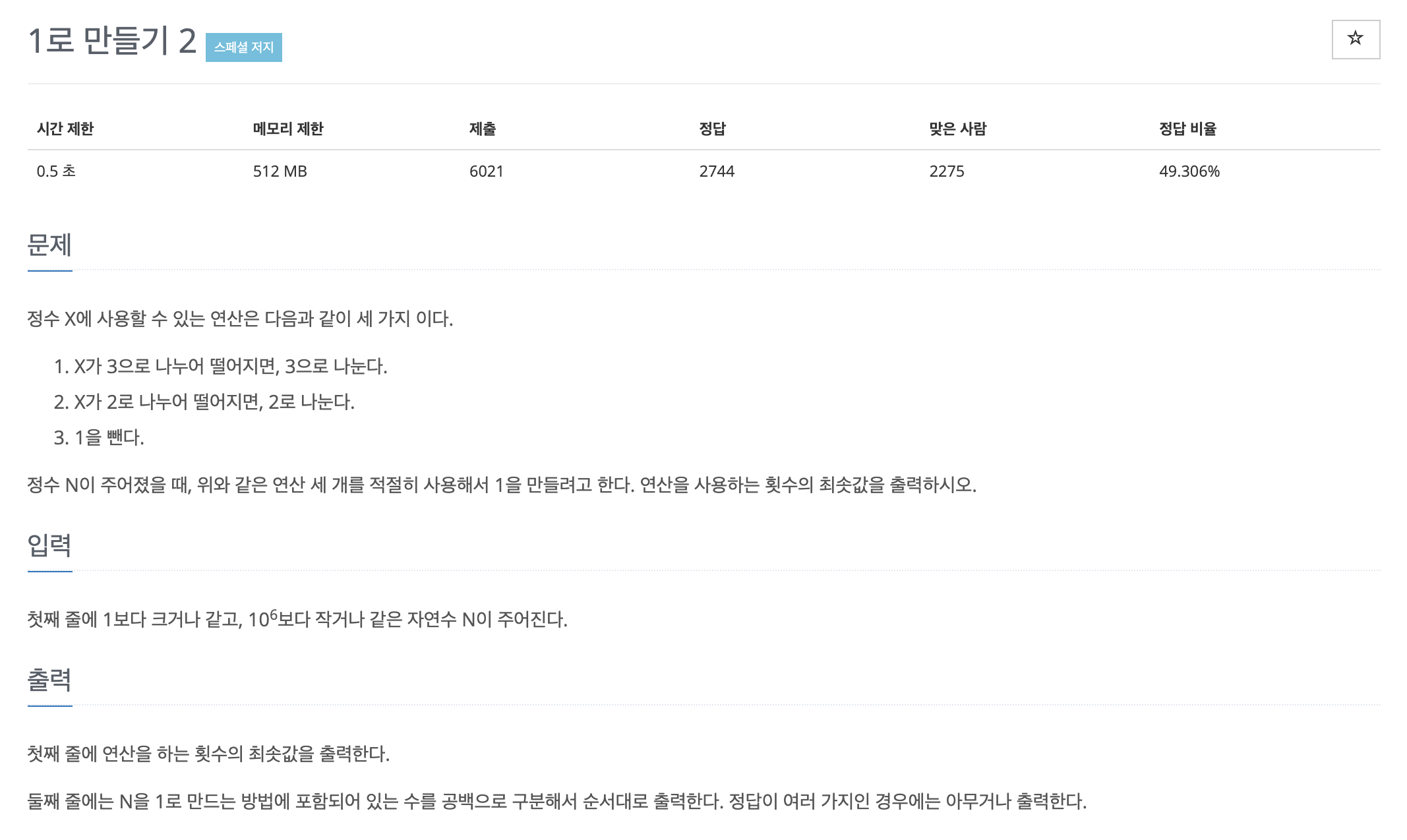
이번 문제는 정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하는 문제입니다.

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 입니다.
1. X가 3으로 나누어 떨어지면, 3으로 나눈다.
2. X가 2로 나누어 떨어지면, 2로 나눈다.
3. 1을 뺀다.

• Java

import java.io.*;
import java.util.*;

public class Main {  
	static int N;
	static int[] dp;
	static final int INF = 1000000000;
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));   
		StringBuilder sb = new StringBuilder();
        
		N = Integer.parseInt(br.readLine()); 
		dp = new int[N + 1];
        
		Arrays.fill(dp, INF);
		dp[N] = 0;
        
		for(int i = N; i >= 1; i--){
			// 현재 i위치에서 가는 최솟값
			int minValue = dp[i] + 1;

			if(i % 3 == 0) dp[i / 3] = Math.min(dp[i / 3], minValue);
			if(i % 2 == 0) dp[i / 2] = Math.min(dp[i / 2], minValue);
            
			dp[i - 1] = Math.min(dp[i - 1], minValue);
		}        

		sb.append(dp[1] + "\n");
        
		int minValue = dp[1];
		Stack<Integer> stack = new Stack<>();

		for(int i = 1; i <= N; i++){
			if(minValue == dp[i]){
				stack.push(i);
				
				if(i*3 <= N && dp[i * 3] == minValue - 1) i = i*3 - 1;
				else if(i*2 <= N && dp[i * 2] == minValue - 1) i = i*2 - 1;
				
				minValue--;
			}
		}
        
		while(!stack.isEmpty()) {
			sb.append(stack.pop() + " ");
		}
        
		bw.write(sb.toString());
        
		bw.flush();
		br.close();
		bw.close();
	}	
}

• Python

import sys

N = int(sys.stdin.readline())
dp = [[0, []] for _ in range(N + 1)] #[최솟값, 경로 리스트]
dp[1][0] = 0 
dp[1][1] = [1]

for i in range(2, N + 1):
	
    #f(x-1) + 1   
    dp[i][0] = dp[i-1][0] + 1
    dp[i][1] = dp[i-1][1] + [i]
    
    #f(x//3) + 1   
    if i % 3 == 0 and dp[i//3][0] + 1 < dp[i][0]:
        dp[i][0] = dp[i//3][0] + 1
        dp[i][1] = dp[i//3][1] + [i]

	#f(x//2) + 1   
    if i % 2 == 0 and dp[i//2][0] + 1 < dp[i][0]:
        dp[i][0] = dp[i//2][0] + 1
        dp[i][1] = dp[i//2][1] + [i]
        
print(dp[N][0])
for i in dp[N][1][::-1]: # 역순 출력
    print(i, end=' ')